Questo articolo tratta un argomento che fa parte dell'algebra superiore e che, quindi, è poco utilizzato nei problemi correnti. Ovviamente, comporta problematiche che non possono essere svolte completamente nel nostro Circolo, ma penso che si possa rendere abbastanza semplice se si rimane nell'ambito della sua applicazione, prendendo per buoni i passaggi più ostici. Per non farci mancare niente mostreremo anche alcuni esercizi risolvibili con l'introduzione di una nuova funzione di tipo esponenziale.

Penso che tutti sappiano cosa s'intende per funzione inversa di una funzione f(x). Essa viene indicata solitamente con il simbolo f^-1. Da punto di vista algebrico se è data la funzione

y = 3x

per ottenere la sua inversa, basta inserire la x al posto della y

x = 3y

e ricavare la nuova y

y = x/3

Questo procedimento si visualizza molto bene passando al piano cartesiano e riportando le due funzioni (Fig. 1).

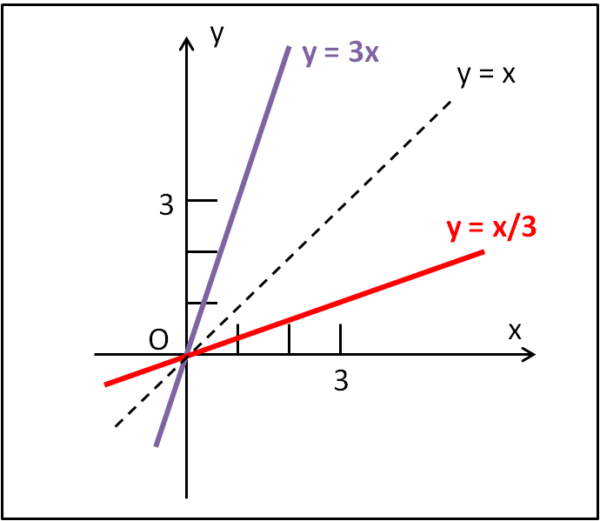
E' immediato notare che le due funzioni (semplici rette in questo caso) sono perfettamente simmetriche rispetto alla retta y = x, ossia alla bisettrice del primo e del terzo quadrante.

Quest'ultima proprietà geometrica vale sempre per qualsiasi funzione e corrispondente funzione inversa.

Per poter esprimere una funzione inversa è necessario che la funzione di partenza sia biunivoca, ossia ad ogni x corrisponda una e una sola y e viceversa. In caso ciò non accadesse si può sempre spezzare la funzione in due parti, ognuna delle quali sia invertibile. Consideriamo un  esempio classico:

y = x²

Ovviamente non è possibile calcolare la sua inversa, dato che uno stesso valore di y si ottiene attraverso due valori di x ( + x e - x). Tuttavia, possiamo sempre limitare il campo di esistenza della x e considerare solo i valori positivi. In tal modo la biunivocità è assicurata e otteniamo il grafico che segue.

Come si scrive la funzione inversa? Facile...

x = y²

y = ???

Accidenti la faccenda non è semplice come nel caso della retta, dato che dobbiamo introdurre una funzione capace di trasformare il quadrato di un numero in tale numero. Beh... tutti sappiamo come fare: basta introdurre la funzione RADICE QUADRATA. Essa risulta essere proprio la funzione inversa dell'elevamento al quadrato. Problema simile si ha, ovviamente, anche per le altre radici.

Proviamo con un'altra funzione

y = e^x

La sua inversa si ottiene invertendo x con y e ricavando y

x = e^y

y = ???

Siamo nuovamente in difficoltà  e dobbiamo nuovamente introdurre una funzione che ci permetta di ottenere quanto si vuole. Nessun problema ci pensa il LOGARITMO NATURALE, ossia

y = ln x

No, non voglio prendere in giro nessuno. Tuttavia, reputo che sia fondamentale capre molto bene ciò che sono alcune funzioni inverse di uso più che comune. Ricordiamoci anche delle funzioni trigonometriche e delle loro inverse, e via dicendo.

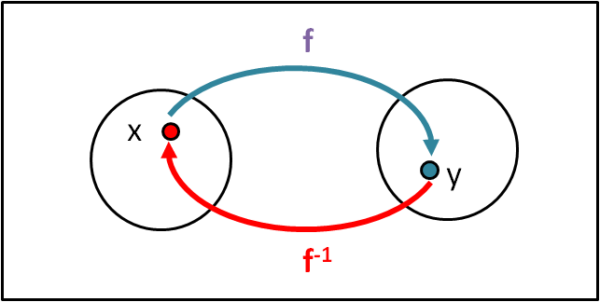
Ritorniamo alla definizione di funzione inversa e ragioniamo nel modo più semplice possibile. Immaginiamo di prendere una certa x in un certo insieme. La funzione f (x) non fa altro che trasformare la x in un nuovo valore y  attraverso una "macchina" che si indica con f. Bene, se la la macchina ha le giuste caratteristiche,  esiste un'altra macchina f^-1 capace di trasformare la y così ottenuta nella vecchia x di partenza. In poche parole applicando la funzione e la sua inversa si ritorna al punto di partenza. Gli esempi fatti precedentemente rispondono a questa necessità.

La Fig. 2 illustra in modo veramente banale quanto detto a parole

Possiamo scrivere, perciò, in termini più "matematici":

f^-1(f(x)) = x

Questa relazione, così banale, è veramente FONDAMENTALE e permette di risolvere moltissimi esercizi.

Ad esempio, vogliamo determinare i valori di x che soddisfano l'equazione:

e^x = 5                           .... (1)

Determinare il valore di x che soddisfa questa equazione

Il sistema da usare è piuttosto semplice... Basta eseguire l'operazione di logaritmo su entrambi i membri:

ln e^x = ln 5

Ricordando la definizione di logaritmo, è immediato scrivere:

x = ln 5                           .... (2)

Abbiamo proprio usato la proprietà della funzione inversa che abbiamo appena definito.

Prima di proseguire ragioniamo un po' su quanto abbiamo dedotto e su quanto facciamo normalmente:

La scrittura della (2) è sufficiente per considerare concluso l'esercizio. Penso che si sia tutti d'accordo a dire di SI, in quanto il secondo membro è una costante ben definita.  Nessuno pretenderebbe di chiederci di calcolare senza alcun aiuto il logaritmo di 5. Basta usare una semplicissima calcolatrice e ricordarsi che la moderna tecnologia ha proprio questo scopo, ossia quello di sveltire i calcoli troppo laboriosi. La stessa cosa capiterebbe per la radice quadrata. Infatti, se trovassimo un risultato del tipo

x = √19

considereremmo risolto il nostro problema.

Esistono metodi capaci di farci calcolare il valore del logaritmo o della radice quadrata di un certo numero, ma sarebbe veramente sciocco fare certi calcoli a mente con passaggi sicuramente lunghi e tediosi e, a volte, nemmeno troppo semplici.

In realtà, qualcuno, in passato, deve aver risolto numericamente queste funzioni "speciali", creando tabelle di grande accuratezza, ma oggi è veramente inutile ripetere il procedimento puramente algebrico che porta al risultato voluto: anche senza pretendere un'intelligenza artificiale, qualsiasi calcolatrice è adatta allo scopo.

Riassumendo:

Se l'incognita da trovare è rappresentata da una costante, calcolabile velocemente con qualche programma di dominio pubblico, la soluzione va considerata come ottenuta.

Con le funzioni che conosciamo e con le loro inverse, è allora possibile risolvere tutti i problemi algebrici di una certa semplicità apparente?

QUIZ

Consideriamo un'equazione apparentemente "innocua"...

2^x + x = 5

Sembrerebbe essere piuttosto facile. Provate a divertirvi ...

Ovviamente, non è ammessa una soluzione puramente grafica. Nulla ci vieterebbe, infatti, di mettere in grafico la funzione y = 2^x + x e la retta y = 5. La loro intersezione darebbe proprio il valore richiesto. Questa soluzione, però, non sarebbe accettabile se fosse necessaria una grande precisione.

In attesa di qualche tentativo tra i più bravi, fermiamoci qui.

continua ....