Forse, qualcuno di voi, leggendo il titolo e dando un'occhiata alla trattazione, avrà storto un po' il naso di fronte alla funzione di Lambert... Vi capisco benissimo... un argomento come quello non può riscuotere molto successo e non è certo ovvio capire la sua importanza.

Tuttavia, questo blog cerca di accontentare un po' tutti, anche le minoranze, per cui reputo giusto proseguire nell'analisi di funzioni molto speciali, cercando di accorciare le parti troppo tecniche (dando magari qualcosa come scontato), e mettere in luce il loro significato attraverso alcuni concetti fondamentali.

Non chiedetemi: "A cosa serve?". La matematica è il linguaggio della fisica e spesso e volentieri questo linguaggio può diventare piuttosto complicato. Per noi il cinese (una lingua difficile, scelta a caso...) è qualcosa di "inutile". Ma non lo è certo per i cinesi... loro la capiscono benissimo e la usano molto spesso!

Guardiamo le cose da un punto di vista più generale e accogliamo (e seguiamo) con interesse l'entrata in ballo di una nuova funzione che riesce a compiere un vero miracolo. E lo fa, anche, in modo estremamente comprensibile. Non spaventatevi per la presenza di integrali... tutto è più semplice di quanto sembri!

Un numero alieno nel mondo dei numeri interi

Questa volta tocca alla Funzione Γ (gamma) di Eulero (figuriamoci se non c'è sempre lui di mezzo) che si prefigge un risultato apparentemente assurdo, ossia il calcolo dei fattoriali di tutti i numeri reali (addirittura complessi). Ricordiamo che l'operazione di fattoriale è definita normalmente per numeri interi maggiori di zero e non è altro che il prodotto di tutti i numeri interi, da quello che si sceglie fino all'unità. In parole matematiche più semplici:

n! = n (n - 1) (n - 2) ..... (2) (1)

Non è certo difficile eseguire il calcolo che è solo e soltanto il prodotto di n numeri interi, da 1 a n. In realtà viene anche definito il fattoriale di 0 (che vale 1), ma ci torneremo a tempo debito.

Non è nemmeno difficile rappresentare questa funzione nel piano cartesiano...

n = 0       0! = 1

n = 1        1! = 1

n = 2        2! = 2 · 1 = 2

n = 3        3! = 3 · 2 · 1 = 6

n = 4        4! = 4 · 3 · 2 · 1 = 24

E' immediato disegnare il grafico in Fig. 1 ...

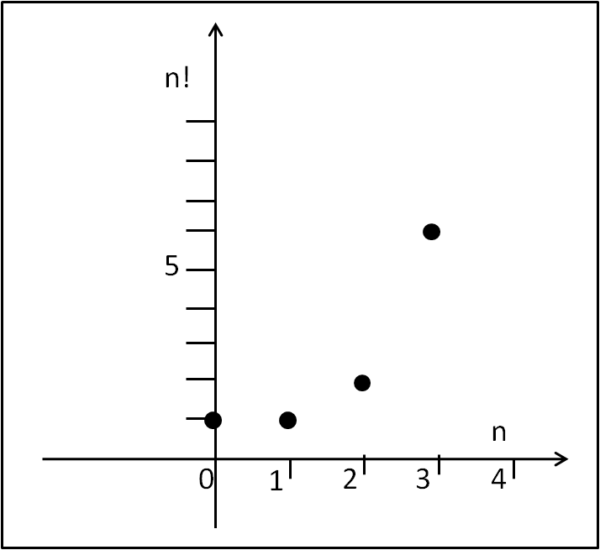
Tuttavia, il grafico è rappresentato solo da punti isolati: la funzione fattoriale NON è continua. Per renderla tale si dovrebbe estendere anche ai numeri non interi compresi in tutti gli intervalli. Ma come fare? Se n fosse uguale a 2/3, quale sarebbe il suo fattoriale? Ciò che si vuole è una funzione CONTINUA che tocchi i punti relativi agli interi e che segua un andamento non dissimile da quanto riescono a fare le funzioni y = x² o y = xⁿ, in genere.

Tralasciamo i termini troppo tecnici e veniamo al sodo... Ciò che vorremmo sarebbe una funzione che interpoli al meglio i punti relativi agli interi. Un artificio matematico, in fondo, ma estremamente utile in matematica (e se lo dice Eulero...). In modo puramente occhiometrico, il risultato non è poi così difficile da ottenere, ma in matematica vogliamo usare l'algebra e soluzioni precise. Potremmo  provare a interpolare i punti con funzioni esponenziali o cose del genere, ma sarebbe una fatica poco utilizzabile. Fidatevi...  conviene seguire il procedimento di Eulero.

Teniamo, comunque, in mente che stiamo praticamente entrando in un nuovo mondo, capace di dare risultati anche dove non dovrebbero esserci: il fattoriale è il regno degli interi, ma noi vogliamo trovare posto anche per chi tale non è. Un alieno per lo spazio dei numeri interi (qualcosa di simile a Flatlandia...).

La funzione gamma è qualcosa di enormemente utile in statistica e in molti altri campi. Essa apre, praticamente, una nuova realtà in modo forse simile alla geometria non euclidea. Permette, infatti, di eseguire operazioni su uno spazio che non è quello "normale". Uno "spazio" in cui è possibile eseguire il fattoriale su numeri reali qualsiasi.

Modifichiamo l'integrale di Gauss

Per iniziare è necessario ricordare un integrale che abbiamo risolto attraverso gli integrali doppi, quello di Gauss. Riportiamolo:

∫_-∞^∞e^{-(x^2)}dx = √π

per comodità di calcolo, dividiamolo "a metà", ossia consideriamolo solo tra 0 e infinito, Esso vale ovviamente:

∫₀^∞e^{-(x^2)}dx = √π/2

Sappiamo, perciò, che questo integrale vale qualcosa di finito e di anche ben conosciuto. Teniamo da parte la soluzione e lavoriamo sulla parte sinistra, ossia sull'integrale vero e proprio...

L'esponente di e è un quadrato. Cambiamolo ponendolo uguale a tx, dove t  è un numero qualsiasi. Niente di male, pur capendo benissimo che il risultato dell'integrazione non sarà più quella dell'integrale di Gauss.

∫₀^∞e^-tx dx

Per come è scritto l'integrale dipende solo da x, e t risulta essere una costante... Inoltre non possiamo più dimenticarci  di agire in modo corretto: l'integrale che ha un limite di integrazione pari a infinito è un integrale improprio e deve essere scritto come limite, ossia:

lim_r→∞∫₀^re^-tx dx

L'integrale è risolvibile immediatamente, ricordando che la derivata di e^-xt è uguale a (-1/t)e^-xt

lim_r→∞ (-1/t)[e^-tx]_o^r

lim_r→∞(-1/t)[e^-tr - e⁰] = lim_r→∞(-1/t)[e^-tr - e⁰] = lim_r→∞(-1/t)[1/e^tr - 1] 

se r tende a ∞, 1/e^tr tende a 1/e^∞, ossia tende a zero. Per cui abbiamo dimostrato che

∫₀^∞e^-tx dx = 1/t

Finora tutto è stato piuttosto semplice. 

Come previsto il nuovo integrale dà un risultato ben diverso da quello relativo all'integrale di Gauss. Tuttavia, non abbiamo ancora visto niente che possa ricondurci al fattoriale. Calma e sangue freddo...

Facciamo un'operazione "ardita": consideriamo t variabile e deriviamo ambo i membri rispetto a t. Per far ciò dobbiamo conoscere la regola di integrazione di Leibniz. Chi vuole può prenderla  "per buona", ma nell'appendice ne diamo una dimostrazione molto semplice, basata solo sulla definizione di derivata. Essa dice che:

d/dt(∫_a^bf(x,t) dx) = ∫_a^b(∂f(x,t)/∂t) dx

Attenzione: la derivata iniziale si applica a un integrale che risulta essere una funzione della sola t. Quella dentro il segno di integrale è una derivata parziale perché si applica a una funzione a due variabili.

Applichiamola al nostro caso e otteniamo:

d/dt(∫₀^∞e^-tx dx) = d(1/t)/dt

∫₀^∞ (∂(e^-tx)∂t) dx = -1/t²

La derivata è parziale e, quindi, x va considerata una costante

∫₀^∞ -x e^-tx dx = -1/t²

A questo punto abbiamo preso gusto a questa simpatica operazione di derivazione. Perché non continuare e derivare un'altra volta? Detto fatto:

∫₀^∞ -x (∂ (e^-tx)∂t) dx = d (-1/t²)dt

∫₀^∞ + x² e^-tx dx = + 2/t³

Facciamo un passaggio quasi ridicolo che però comincia a svelare dove vogliamo arrivare:

∫₀^∞ + x² e^-tx dx = +(1 · 2)/t³

Capita l'antifona? Non ancora?  Va beh... deriviamo ancora una volta...

∫₀^∞ - x³ e^-tx dx = - (1 · 2 · 3)/t⁴

Non ci reste che riflettere e tirare le somme.

Cominciamo dal segno. Una volta è positivo e una volta è negativo. Quando x ha esponente dispari diventa negativo. Possiamo perciò indicarlo utilizzando la relazione: (-1)ⁿ xⁿ. Se n è pari il segno diventa +, se è dispari diventa -. Il segno del secondo membro segue la stessa regola. Dopo di che dobbiamo scrivere il prodotto di 1 per 2 per 3, ecc. Quante volte? Tante quante dice n, ossia otteniamo n!. Infine il denominatore vale, ovviamente, (n + 1).

Ne segue:

∫₀^∞ (-1)ⁿ xⁿ e^-tx dx = ( -1)ⁿ n!/t^{(n + 1)}

Semplifichiamo, eliminando (-1)ⁿ, e abbiamo:

∫₀^∞  xⁿ e^-tx dx = n!/t^{(n + 1)}

A questo punto conviene chiamare n come z - 1 e la relazione diventa

∫₀^∞  x^{(z - 1)} e^-tx dx = (z - 1)!/t^z

Torniamo all'inizio. Ricordiamoci che abbiamo considerato t qualsiasi. Nulla ci vieta di porla uguale a 1. Cosa otteniamo:

∫₀^∞  x^{(z - 1)} e^-x dx = (z - 1)!/1^z

uno, elevato a qualsiasi numero reale, è sempre uguale ad uno

∫₀^∞  x^{(z - 1)} e^-x dx = (z - 1)!

Abbiamo  ottenuto ciò che volevamo. Il primo membro prende il nome di Funzione Gamma; essa si indica con Γ, ed è uguale a (z -1)!

Γ(z) = (z - 1)!

Questa relazione vale per qualsiasi z reale (ma anche complesso) e descrive la funzione continua che interpola al meglio i punti descritti dal fattoriale dei numeri interi. In realtà, la Γ(1) = 0! = 1, la Γ(2) = 1! = 1, Γ(3) = 2! = 2, Γ(4) = 3! = 6 e via dicendo. Basta calcolare la Γ per ogni valore che vogliamo, attraverso l'integrale, e si ottiene la curva di Fig. 2

Da gamma al fattoriale il passo è breve

Poniamo x = t (il vecchio t non serve più) e z = x per evidenziare meglio la continuità della funzione, ossia per mettere in evidenza che x (il vecchio z) non è un intero, ma un numero reale qualsiasi.

Γ(x) = ∫₀^∞  t^{(x - 1)} e^-t dt = (x - 1)!

Se vogliamo proprio calcolare x!, dobbiamo solo aumentare di 1 la x sia a sinistra che a destra, ossia:

Γ(x + 1) = ∫₀^∞  t^x  e^-t dt = x!

La Fig.3 che segue mostra la funzione gamma e la funzione fattoriale.

Esse sono praticamente la stessa funzione e ciò che cambia è solo l'origine degli assi.  Notiamo, però, che questo "spostamento" fa sì che sia possibile calcolare la funzione gamma anche dei numeri positivi minori di uno, il che corrisponde al fattoriale di un numero negativo, compreso tra 0 e -1. Calcolare gamma per la zona rosa vuol dire calcolare il fattoriale di numeri non interi e negativi.

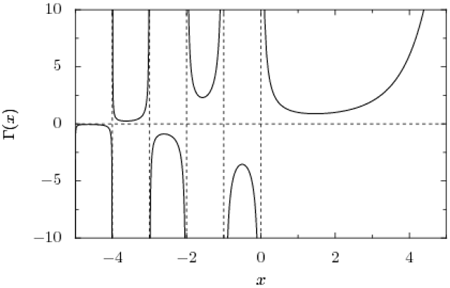
In realtà, la funzione gamma va ben oltre e può essere calcolata (data la sua definizione) per tutti i numeri negativi, tranne che per gli interi negativi, dove la funzione va ad infinito. Tra poco lo dimostreremo. Per adesso  ammiriamo la Fig. 4 dove è rappresentata la funzione gamma dei numeri reali positivi e negativi.

Qualche esempio per costruirla

Innanzitutto, è facile dimostrare subito perché 0! vale proprio 1. Infatti, basta calcolare la funzione gamma per il valore 1 e ciò che otteniamo è proprio il fattoriale di  x - 1 = 1 - 1 = 0.

Γ(1) = ∫₀^∞  t^{(1 - 1)} e^-t dt = (1 - 1)!= 0!

0! = Γ(1) = ∫₀^∞  e^-t dt = [- e^-t]₀^∞ = [ - 1/e^t]₀^∞ = - 0 -(-1/1) = 1 

Passiamo ora a un numero frazionario, ossia a 1/2 (che è poi il valore di (-1/2)!).

Γ(1/2) = ∫₀^∞  t ^{(1/2 - 1)}  e^-t dt =∫₀^∞  t ^-1/2  e^-t dt

poniamo

u² = t

t^-1/2 =u^2(-1/2)

dt = 2 u du

Per cui

Γ(1/2) = 2∫₀^∞  u^2(-1/2) e^{-u^2} u du = 2∫₀^∞  u^-1 e^{-u^2} u du = 2∫₀^∞ e^{-u^2} du

Ma il secondo membro è una vecchia conoscenza essendo l'integrale di Gauss. Sappiamo bene che vale √π/2

Ne segue:

Γ(1/2) = 2 √π/2 = √π

Divertiamoci un poco con la relazione

Γ(x) = (x - 1)!

Possiamo scrivere:

Γ(x + 1) = (x )!

ma anche

Γ(x + 1)  = x (x - 1)!

Γ(x + 1)  = x Γ(x)

Γ(x) = Γ(x + 1)/x

Poniamo x = 0

Γ(0) = Γ(0 + 1)/0 = Γ(1)/0

Abbiamo appena calcolato che

Γ(1) = 1

per cui

Γ(0) = 1/0 = ∞

Elementare Watson!

 

Calcoliamo adesso, in modo simile, la funzione gamma di 3/2, che corrisponde, ovviamente, a (1/2)!

Γ(x + 1) = x! = x (x - 1)! = x Γ(x)

Γ(x + 1)  = x Γ(x)

3/2 = 1 + 1/2

Γ(1/2 + 1) = Γ(3/2) = 1/2 Γ(1/2) = √π/2 

 

E' banale proseguire e calcolare Γ(5/2)

Γ(5/2) = Γ(3/2 + 1) = 3/2 Γ(3/2) = (3/2) (√π/2 ) = 3 √π/4 

e poi Γ(7/2) ...

Γ(7/2) = (5/2)(3/4) √π = 15 √π /8

e così via...

 

Non è nemmeno difficile calcolare la funzione gamma di un numero negativo (diverso da un intero). Ricaviamola per -1/2

Abbiamo appena visto che:

Γ(x) = Γ(x + 1)/x

mettendo -1/2 al posto di x

Γ(-1/2) = Γ(-1/2+ 1)/(-1/2) = - Γ(1/2)/(1/2) = - 2√π

Potete divertirvi a trovare  la funzione gamma per altri valori frazionari di x...

E' anche immediato capire perché la funzione di tutti igli interi negativi va sempre a infinito, sapendo già che Γ(0) = ∞.

Γ(-1) = Γ(- 1 + 1)/-1 = Γ(0)/ - 1 = ∞/-1 = ∞.

In modo analogo i verifica per tutti gli interi negativi.

Ovviamente, su Internet potete trovare i siti dove inserendo un numero qualsiasi vi viene restituita la funzione gamma relativa (e quindi anche il fattoriale). In modo simile a quanto viene fatto per la funzione di Lambert.

Chi vuole divertirsi in modo più "elaborato", può anche cercare di ricavare direttamente (1/2)! . Un esercizio un po' complicato che sfrutta l'integrazione per parti... Lo trovate come Appendice 2.

 

Appendice 1: La Regola di Leibniz **

ho una funzione a due variabili f(x,t) e voglio conoscere la derivata rispetto a t dell'integrale di questa funzione .

d/dt (∫_a^bf(x,t) dx)

Attenzione: ho scritto d e non ∂ in quanto l'integrale è una funzione della sola t.

Consideriamo il grafico con ascissa x e ordinata f(x, t).

 

L'integrale tra a e b è l'area sotto la curva blu.

Per un certo valore t + Δt la funzione diventa la curva rossa e il suo integrale è tutto ciò che sta sotto di lei.

Ma la derivata non è altro che il limite del rapporto incrementale. Nel nostro caso, è in pratica la differenza tra le due aree diviso Δt :

d/dt (∫_a^bf(x,t) dx) = lim _Δt→0 (∫_a^b (f(x, t + Δt) dx - ∫_a^b f(x,t)) dx)/Δt

Tuttavia, applicando la serie di Taylor per funzioni a due variabili, possiamo scrivere:

f(t + Δt, x) = f(x,t) +  (∂f(x,t)/∂t) Δt

il termine in x non compare in quanto la x non varia

Inseriamo questa espressione dentro  il nostro limite

(∫_a^b((f(x, t + Δt) dx - ∫_a^bf(x,t)) dx)/Δt = (∫_a^b(f(x, t)+ ∂f(x,t)/∂t) Δt)dx  - ∫_a^b f(x,t) dx)/Δt

Ma ∫f(x,t) si semplifica e resta

∫_a^b(∂f(x,t)/∂t  Δt dx) /Δt

Ossia

∫_a^b (∂f(x,t)/∂t dx

In conclusione:

d/dt (∫_a^bf(x,t) dx) = ∫_a^b(∂f(x,t)/∂t) dx

 

Appendice 2. Calcolo diretto di (1/2)! (per chi vuole divertirsi con l'integrazione per parti) ***

Iniziamo, ricordando che vogliamo calcolare il fattoriale di 1/2. Come lo possiamo scrivere? Facile, basta ricordarsi che

x! =  ∫₀^∞  t^x  e^-t dt

Imponiamo x = 1/2

(1/2)! = ∫₀^∞  t^1/2 e^-t dt

Conviene cambiare variabile e porre u = t^1/2

il che comporta che  u² = t e, ancora, differenziando:

2 u du = dt

Andiamo a sostituire

(1/2)! = ∫₀^∞ u e^{-u^2} 2 u du = 2∫₀^∞ u² e^{-u^2} du              .... (1)

Non abbiamo dovuto cambiare i limiti di integrazione dato che anche u va a zero e infinito come t.

Ed eccoci di fronte a un serio ostacolo... abbiamo il fattore u² che dà parecchio fastidio. E non è certo possibile scrivere che l'integrale di un prodotto è uguale al prodotto degli integrali!

Tuttavia, possiamo, comunque, scrivere l'integrale "spezzando" u² in due parti

(1/2)! = 2∫₀^∞ u u e^{-u^2} du                 

Notiamo che la parte in azzurro è un integrale che si può calcolare molto bene, mentre u può essere derivata facilmente

Calcoliamo l'integrale della parte azzurra. Cambiando momentaneamente variabile si semplifica il procedimento:

v = - u²

dv = - 2 u du

-1/2 dv = u du

∫ u e^{-u^2} du = ∫ -1/2 e^v dv = -1/2 e^v

trascuriamo pure la costante  dato che passeremo subito a integrali definiti.

Torniamo alla nostra u e l'integrale appena calcolato vale -1/2 e ^{-u^2}

L'integrazione per parti ci dice che siamo nelle giuste condizioni

Ricordiamo la strategia dell'integrazione per parti:

∫_a^bf(u)g'(u) du = [f(u)g(u)]_a^b - ∫_a^b f '(u) g(u) du

Nel nostro caso

f(u) = u

f '(u) = 1

g'(u) =  u e^{-u^2}

g(u) = ∫₀^∞ u e^{-u^2} =  -1/2 e ^{-u^2}

∫₀^∞ u ue^{-u^2} du = [(u) (-1/2 e^{-u^2} )]₀^∞ - ∫₀^∞ (1) (- 1/2 e ^{-u^2}) du 

∫₀^∞ u²e^{-u^2} du =  [-u/2e^{u^2}]₀^∞ + 1/2∫₀^∞ e ^{-u^2} du

Studiamo la prima parte del secondo membro...

[-u/2e^{u^2}]₀^∞

per u che tende a infinito è immediato dire che il denominatore tende a infinito molto più velocemente del numeratore, per cui il rapporto vale 0. Per u che tende a 0, il numeratore vale 0, mentre il denominatore vale 1, per cui il rapporto è ancora una volta zero. Rimane perciò solo la seconda parte del secondo membro, ossia:

∫₀^∞ u²e^{-u^2} du = 1/2∫₀^∞ e ^{-u^2} du

Ma noi conosciamo molto bene il secondo membro, infatti ∫₀^∞ e ^{-u^2} du è proprio l'integrale di Gauss e sappiamo che vale √π/2

Possiamo finalmente scrivere il fattoriale di 1/2, ricordando la (1)

(1/2)! = 2 ∫₀^∞ u²e^{-u^2} du = 2 · 1/2 · √π/2

(1/2)! = √π/2 ≈ 0.8862 ...