Oggi sappiamo bene che esistono geometrie non euclidee. Proprio per cercare di dirimere il problema collegato al quinto postulato di Euclide (quello dell'esistenza di una sola parallela a una retta data passante per un punto) si è arrivati alla geometria iperbolica (ne parleremo sicuramente presto) e poi alla geometria sferica, fondamentale per giungere alla relatività generale. Argomenti complicati che nascondono però altre possibilità sicuramente più semplici. Proprio Minkowski, il grande scienziato che ha applicato la geometria iperbolica alla rappresentazione grafica della relatività ristretta, ha ideato una geometria piana adottando una metrica del tutto diversa con risvolti pratici estremamente utili anche ai giorni nostri. Vediamo di arrivarci per gradi...

Vi ricordate il paradosso della scala e della formica? No? Andate a (ri)leggerlo e troverete spiegato in modo abbastanza semplice che il paradosso non è tale, ma si è di fronte a due funzioni differenti che non possono mai sovrapporsi, neanche andando all'infinito.

Lo stesso "paradosso", però, potrebbe risolversi considerando la congiungente A con B come singola funzione (un segmento di retta), ma cambiando la metrica che definisce le distanze tra punti.  Lo "spazio" è sempre quello euclideo, ma cambia il modo di definire le distanze.

Questa nuova geometria prende il nome di taxicab geometry, ossia geometria del tassista, No, non consideriamola solo un gioco geometrico-matematico, dato che ha delle ricadute pratiche estremamente utili nella vita di tutti i giorni. I tassisti, ad esempio, la conoscono piuttosto bene e la usano costantemente.

Pensiamo a come è nata la geometria euclidea... Non esistevano ancora le grandi città metropolitane e, soprattutto, esistevano spazi vuoti e pianeggianti, ideali per tracciare rette, triangoli, circonferenze seguendo quella che sarebbe diventata la metrica euclidea. Ciò era più che vero già dai tempi delle prime civiltà.

Consideriamo ad esempio, uno dei concetti più banali... Dati due punti qualsiasi la loro distanza minima è misurata dalla lunghezza del segmento rettilineo che li unisce. Ottimo. Con questa definizione posso misurare la distanza tra due punti partendo da uno di essi e portandomi sull'altro lungo l'unica retta che li unisce. Immaginiamo, però, che i due punti siano separati da un ostacolo insormontabile, ad esempio il palazzo del Faraone. Non possiamo certo pensare di attraversare il palazzo in linea retta. In qualche modo, devo misurare la distanza aggirando l'ostacolo. Esisterà una distanza minima "percorribile", ma non ha niente a che fare con la distanza della geometria euclidea.

Immaginiamo, ancora, che tutto lo spazio piano percorribile sia coperto da edifici e che ci si possa muovere solo lungo delle "strade" tra loro perpendicolari. Molte città romane erano costruite in questo modo, così come lo sono, più o meno, le grandi metropoli odierne.

Possiamo disegnare una loro mappa come in Fig. 1.

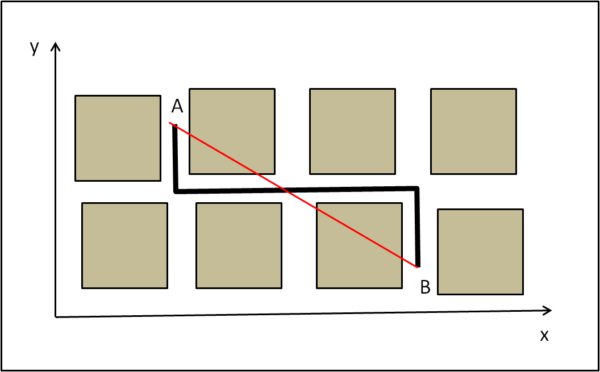
Se vogliamo andare dal punto A al punto B, velocemente, sprecando cioè il minor tempo possibile, ci conviene usare la macchina e, se non l'abbiamo, chiamare un taxi. Vi è bisogno di dire al taxista la strada da percorrere? Normalmente no e lui effettuerà il suo servizio utilizzando un concetto di distanza del tutto personale e non euclideo, che conosce molto bene, anche se non se ne rende -forse- nemmeno conto.

Possiamo muoverci come vogliamo per andare da A a B? Assolutamente no! E' possibile solo utilizzando tratti di percorso paralleli ai due assi x e y. Tradotto in termini della famosa formica e della scala, per andare da A a B la formica è costretta ad usare una scala definita da una serie di scalini più o meno numerosi, che, comunque portano a una sola distanza finale, ben diversa da quella che utilizzerebbe se tutte le traiettorie fossero consentite. In altre parole, la formica deve seguire la strategia del tassista, avendo però a disposizione infinite strade perpendicolari tra loro. La distanza percorsa, scegliendo qualsiasi reticolato di strade, sarebbe sempre uguale alla somma tra la distanza misurata lungo l'asse y e quella misurata lungo l'asse x. In termini matematici (molto semplici) la distanza euclidea d_E tra A e B (sempre positiva ovviamente)

d_E = √((xB - xA)² + (yB - yA)²)

diventerebbe d_T

d_T = |xB - xA| + |yB - yA|.

In altre parole, muoversi su una retta vorrebbe dire muoversi lungo una scala con infiniti  (o anche uno solo) scalini tra A e B.

"Risolto" il problema della formica, allarghiamo la visuale verso questa nuova interessantissima metrica e vediamo  come, e se, sia possibile costruire le figure tipiche della geometria euclidea e quali teoremi o criteri valgano ancora oppure no.

Ed eccoci al nostro "quiz" sulla quadratura del cerchio...

Abbiamo visto che tracciando un segmento di retta euclidea, essa ha ancora lo stesso significato, ma ciò che cambia è la distanza tra gli estremi. E se disegnassimo una circonferenza euclidea, essa sarebbe sempre tale anche nella nuova geometria? Saremmo costretti a dire di no, tenendo presente la definizione di circonferenza. Consideriamo, infatti, la Fig. 2 in cui è disegnato un cerchio di raggio r  e di centro O.

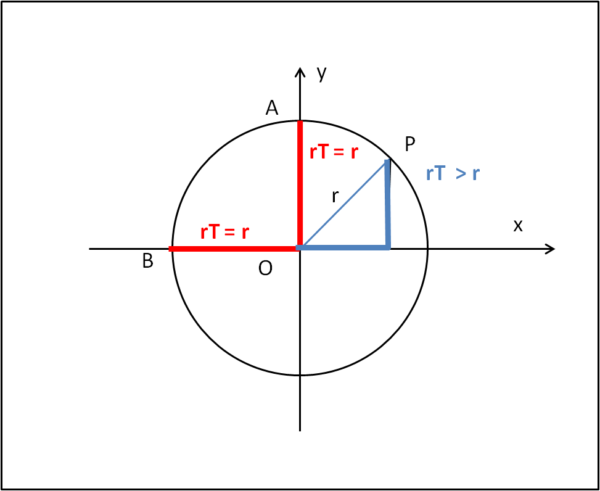
Beh, i suoi punti avrebbero distanze ben diverse dal centro. Quelli posti sugli assi avrebbero distanza r, come desiderato, ma tutti gli altri avrebbero distanze r_T sempre maggiori di r, come dimostra la linea azzurra che definisce la distanza di P dal centro.

A questo punto ci chiediamo: "E' possibile, con la nuova metrica, dato un punto O, costruire una e una sola circonferenza di raggio r_T" ? Il che sarebbe poi il terzo postulato di Euclide...

La risposta è SI, anche se  subirà delle limitazioni di "orientamento" e se cambierà (in meglio ...) la costante pi greco.

Vediamo come fare, utilizzando la nuova metrica.

Consideriamo un punto O come centro. Per semplicità lo poniamo proprio nell'origine degli assi (Fig. 3).

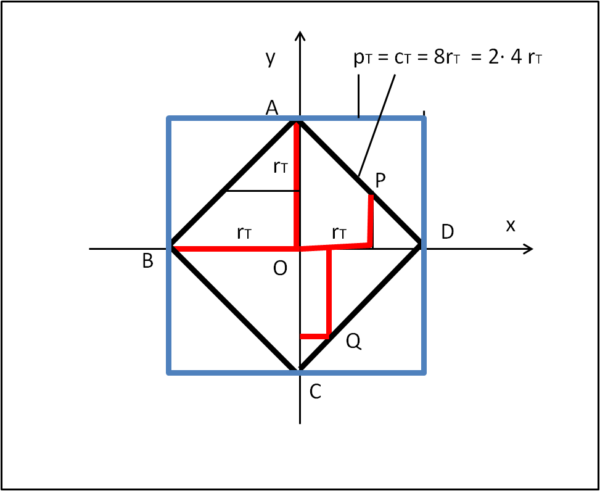
Disegniamo quattro raggi di questa circonferenza, muovendoci proprio nelle direzione degli assi. Otteniamo i punti A,B,C e D che distano proprio r_T da O. Fino a qui abbiamo seguito esattamente Euclide. Da adesso in poi, però, il compasso perde di significato. Quanto vale il raggio nel nostro caso?

Qualsiasi altro punto P della circonferenza deve trovarsi a una distanza r_T dal centro. Non è certo difficile ottenere quanto voluto, ricordando la definizione di distanza d_T.

E' immediato disegnare i punti della "circonferenza", ossia dei punti aventi la stessa distanza d_T dal centro. Ovviamente, posso imporre qualsiasi x voglia e ottenere la rispettiva y, anche usando numeri non interi. L'importante è che la somma dei loro valori assoluti dia come risultato il raggio, ossia una distanza d_T = r_T.

Ed ecco, in nero, la circonferenza relativa alla nuova metrica. Chiamiamola c_T.

E' facile misurare la lunghezza della circonferenza. Essa vale c_T = 8r_T. Per Euclide il rapporto tra lunghezza della circonferenza e il raggio valeva

2πr/r = 2π

Con la nuova metrica, per qualsiasi circonferenza, vale la relazione

c_T/r_T = 8r_T/r_T = 8

Il nuovo pi greco è diventato 4 !!!

Tornando al nostro quiz. La lunghezza della circonferenza con la nuova metrica è un numero intero perfetto ed è altrettanto perfetto il quadrato che ha per perimetro lo stesso identico valore. Detto in altre parole: data una circonferenza qualsiasi è sempre possibile costruire, con riga non graduata e compasso,  un quadrato azzurro che abbia la circonferenza come perimetro p_T.

Come sarebbe bello utilizzare un π così semplice! Purtroppo, la faccenda è più complicata. La circonferenza che abbiamo tracciato poco fa può essere traslata nel piano, ma NON può essere ruotata, in quanto cesserebbe di essere una circonferenza.  L'esistenza della circonferenza è vincolata all'orientamento rispetto agli assi di riferimento, ossia alle strade del tassista.

 

A livello più o meno elementare è divertente andare ancora oltre e rappresentare l'asse di un segmento, la perpendicolare, il triangolo, stabilire se valgono ancora certi criteri a loro relativi, costruire tutte le coniche e chi più ne ha più ne metta. Potete divertirvi da soli e studiare le situazioni più "imbarazzanti" (al limite chiedete aiuto a un ... tassista!). Se l'argomento vi interessa, potrei anche proseguire nella trattazione. Aspetto le vostre reazioni a riguardo...

Per adesso vi propongo un "quiz" che forse non è poi così semplice come sembra. Sappiamo tutti che l'asse di un segmento è la perpendicolare al segmento passante per il suo punto di mezzo. Bene, nella Fig. 4  sono rappresentati 5 segmenti AB (in pratica è lo stesso segmento ruotato).

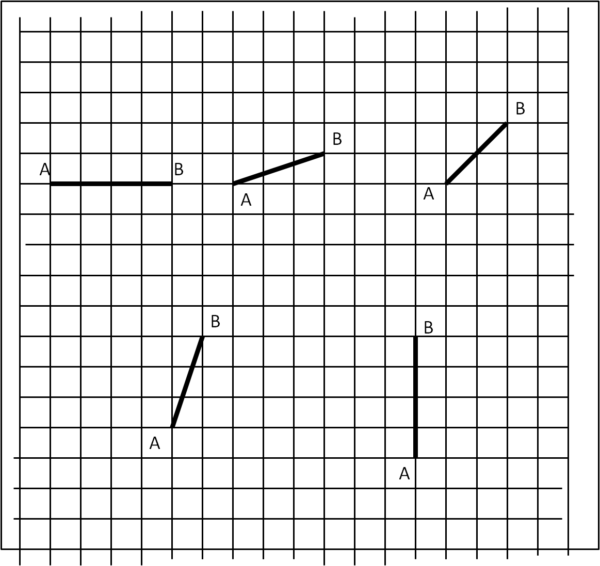
Ciò che vi chiedo è di disegnare gli assi di questi segmenti. Euclide l'avrebbe saputo fare con la riga e il compasso, ma a noi il compasso non serve più... Ho inserito, infatti,  una grata secondo gli assi x e y per facilitare la soluzione.

continua ...?

P.S.: avete notato che l'articolo ammette come difficoltà un solo asterisco così come anche tre e forse più. Ciò dipende dal fatto che tale metrica può portare a teoremi e configurazioni anche estremamente complicati. Magari proprio quelli che bisognerebbe inviare nello spazio alla ricerca di alieni abituati a vivere soltanto in centri iper-affollati...

P.S. 2: chi è interessato a svariati metodi per avvicinarsi alla quadratura o alla rettificazione, può divertirsi QUI