Finalmente abbiamo superato l'ostacolo della mancanza di compasso. La chiave del problema è una proprietà dei trapezi qualsiasi, forse poco conosciuta: la retta che passa per l'intersezione delle diagonali e per l'intersezione dei prolungamenti dei lati non paralleli divide a metà le basi del trapezio. Iniziamo dimostrandola...

Disegniamo il trapezio QNSR in Fig. 1.

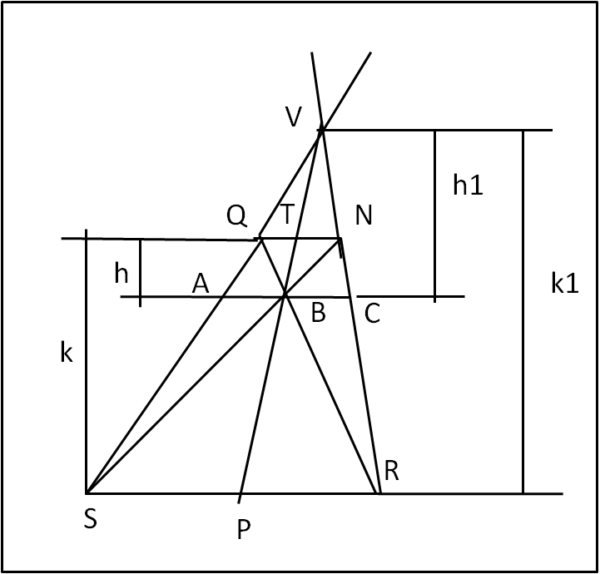
Tracciamo le due diagonali QR e  SN che si incontrano in B. Da B tracciamo la parallela a SR che incontra i due lati del trapezio in A e C. Ne segue immediatamente che i triangoli AQB e SQR, così come BNC e SNR, sono simili (due angoli uguali). Possiamo perciò scrivere:

AB/SP = h/k

BC/SR = h/k

Da cui

AB = BC

I triangoli VAB e VSP sono simili, così come VBC e VPR

Ossia:

AB/SP = h1/k1

BC/PR = h1/k1

Ma abbiamo appena dimostrato che AB = BC, per cui:

SP = PR

Analogamente:

QT = TN.

Conosciuta questa proprietà è facile applicarla al nostro caso...

Disegniamo la Fig. 2 con la retta r e il segmento AB, ad essa parallelo.

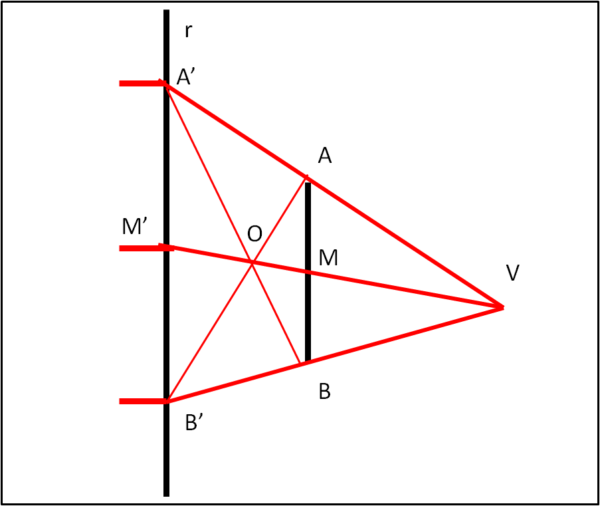
Scegliamo due punti qualsiasi A' e B' sulla retta r e uniamo A' con A e B' con B. Sia V il punto della loro intersezione. Individuiamo il trapezio A'ABB'. Tracciando le sue diagonali e uniamo V con O. Per quanto dimostrato prima M' divide esattamente a metà il segmento A'B'.

Otteniamo due nuovi trapezi (A'AMM' e M'MBA), per cui, ripetendo per entrambi l'operazione precedente, determiniamo i punti medi tra A' e M' e tra M' e B'. Continuando con questa procedura arriviamo a costruire la Fig. 3, dove il segmento A'B' è stato diviso in 8 parti uguali.

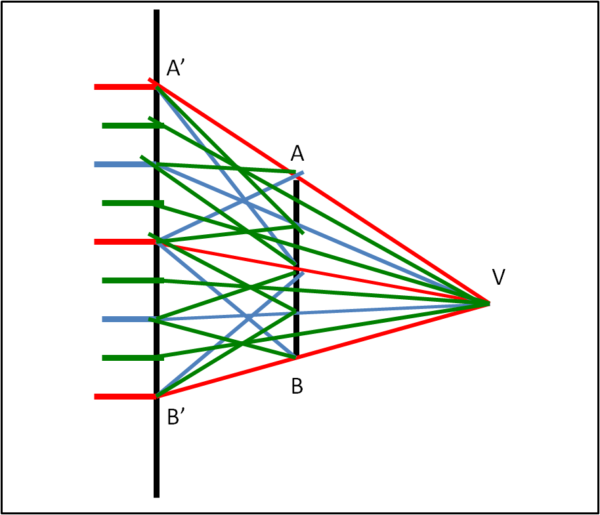
Se il numero di divisioni da imporre ad AB fosse pari a 8, avremmo già risolto il problema. Noi ne vogliamo solo 7. Banale... basta utilizzare la Fig. 4

Consideriamo il punto Z' in modo che il segmento A'Z' sia diviso in 7 parti. Uniamo A' con A e Z' con B, individuando il punto V'. Tracciano le rette che da ogni punto dei sette intervalli di A'B' arriva in V'. Come conseguenza divideremo in 7 parti anche il segmento AB. Prendendo solo 5 parti di A'B', divideremmo AB in 5 e via dicendo.

In realtà, non abbiamo proprio "superato" Euclide e il suo compasso, avendo dati per già tracciati retta e segmento PARALLELI. Se Euclide avesse avuto un foglio di carta avrebbe potuto piegarlo e, in trasparenza, disegnare un segmento parallelo a r, prima di riaprire il foglio, ma avrebbe compiuto un'azione meccanica e questo non era permesso. Va bene, molto bravi, comunque, sprmnt21 e Rocco!