Categorie: Matematica
Tags: geometria perimetro minimo quiz triangolo triangolo inscritto
Scritto da: Vincenzo Zappalà
Commenti:11
(QI) Un triangolo dentro a un triangolo ***
Nel 1775 è stato proposto un problema di geometria "elementare" che è stato risolto in vari modi. Esso dice:
“In un dato triangolo acutangolo, inscrivere un triangolo il cui perimetro sia il minimo possibile”
Provate a risolverlo da soli, ma, solo e soltanto, con la pura geometria. Insomma, nessun "calcolo" analitico.
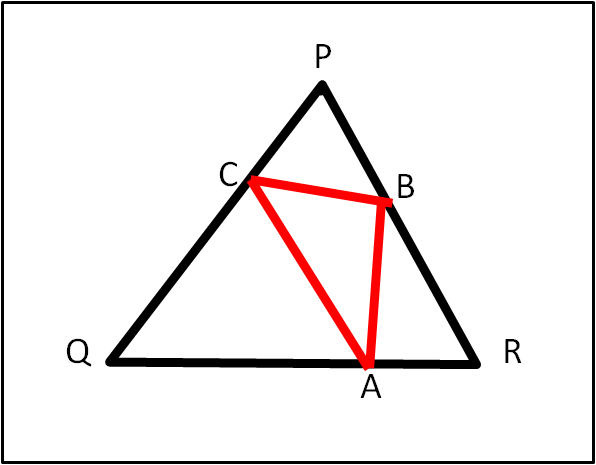
Ovviamente, bisogna anche dimostrare che la soluzione sia corretta!






11 commenti
E' il triangolo avente vertici nei punti estremi delle altezze condotte dai tre vertici del triangolo di partenza.
Tali altezze costituiscono ovviamente bisettrici degli angoli del nuovo triangolo.
I rimanenti 3 triangoli formatisi sono tutti simili a quello di partenza.
Così credo.
Per la dimostrazione, ho chiamato Erone ma si è negato ...
Bye
L'idea (buona?) credo sia quella delle palle da biliardo (carambola, ad esempio) o la riflessione di un raggio di luce.
I lati del triangolo cercato devono formare angoli uguali con il lato dove si "appoggiano" (proprio come farebbe un raggio di luce su uno specchio) o una palla di biliardo (biliardo triangolare in questo caso) che rimbalza sulla sponda.
Poi cerco di tradurre in termini geometrici la pensata.
Il triangolo minimale è quello azzurro, con i vertici sui piedi delle altezze del triangolo dato (costruito, ad esempio, con le intersezioni della semicirconferenza di diametro AB con i lati AC, BC e similari)
Il perimetro di questo (per evidenti simmetrie) è uguale al segmento D'D'1.
Se partendo dal punto D si traccia un diverso triangolo (porpora) si trova che il perimetro è uguale alla spezzata
D'IHD'1 che evidentemente è maggiore del segmento D'D'1.
mi manca ancora un pezzo per chiudere la prova.
Direi che tu hai dimostrato, per adesso, quale è il perimetro minore di un triangolo qualsiasi che tocchi il triangolo originale in D. In realtà bisogna trovare il perimetro minimo anche facendo variare D ... Sì, temo che manchi ancora qualcosa...
Dato il triangolo ABC sia N un punto su BC , N’ il simmetrico di N rispetto ad AB, N’’ il simmetrico di N’ rispetto ad AC e D l’intersezione tra AB ed N’N’’.
Da <BAN = <N’N’’N segue che DAN’’N è ciclico.
Pertanto <ANN’’ = <ADN’’ = 90 - <A.
In altre parole l’angolo <ANN’’ non dipende dalla posizione di N su BC.
Se scegliamo R il piede dell’altezza da A su BC, con la stessa costruzione seguita per N, otteniamo il punto R’’.
Per quanto provato <ARR’’ = 90 - <A.
Quindi i due triangoli isosceli ARR’’ ed ANN’’ sono simili. Essendo AR < AN segue che RR’’ < NN’’ per ogni N =/= R.
Ma come si verifica facilmente con le proprietà di simmetria
RR’’ = perimetro(RMQ)
e similarmente
NN’’ = perimetro (NPQ).
Cioè il triangolo RMQ è quello di perimetro minimo tra tutti quelli costruiti con le “riflessioni” opportune partendo da un punto N qualsiasi.
Per quanto visto nel messaggio precedente per ogni punto N il triangolo costruito con le opportune “riflessioni” ha perimetro minore di qualsiasi triangolo inscritto in ABC che abbia vertice in N.
Tralasciando le dimostrazioni con l'utilizzo delle simmetrie assiali et al., note in letteratura, si può dimostrare in altro modo.
Il percorso QRP è chiuso e deve essere minimo.
Pertanto, come ben noto, gli angoli di incidenza e di riflessione (ed i complementari) devono essere uguali.
Quindi i 3 triangoli esterni (APQ etc) devono essere necessariamente simili.
E ciò avviene se e solo se i vertici del triangolo cercato sono posti sui piedi delle altezze del triangolo di partenza.
Saluti
cari amici,
il risultato è giusto, ma le dimostrazioni non sono spiegate in modo veramente accessibile a chi non ha le vostre conoscenze... Le soluzioni devono permettere di comprendere con estrema semplicità i vari passaggi. La geometria, per essere amata, deve mostrarsi nella sua veste più facile (quando è possibile). Comunque, bravi come sempre!
Non so come "tagliare" il dettaglio della spiegazione per essere pienamente "accessibile", dipendendo questo
da cose e contesti che non conosco. Provo comunque ad aggiungere qualche spiegazione di qualche passo.
[Vedi figura 1 del post precedente]
Dato il triangolo ABC sia N un punto su BC , N’ il simmetrico di N rispetto ad AB, N’’ il simmetrico di N’ rispetto ad AC e D l’intersezione tra AB ed N’N’’.
Per costruzione il punto A è il centro del cerchio circoscritto al triangolo NN’N’’.
Per la proprietà delgi angoli alla circonferenza, l’angolo al centro <N’AN è il doppio del corrispondente angolo alla circonferenza <N’N’’N.
Per simmetria <N’AN = 2<BAN, da cui <BAN = <N’N’’N.
Da <BAN = <N’N’’N segue che DAN’’N è ciclico.
Pertanto <ANN’’ = <ADN’’ = 90 - <A.
In altre parole l’angolo <ANN’’ non dipende dalla posizione di N su BC.
[Vedi figura 2 del post precedente]
Se scegliamo R il piede dell’altezza da A su BC, con la stessa costruzione seguita per N, otteniamo il punto R’’.
Per quanto provato <ARR’’ = 90 - <A.
Quindi i due triangoli isosceli ARR’’ ed ANN’’ sono simili. Essendo AR < AN segue che RR’’ < NN’’ per ogni N =/= R.
Ma come si verifica facilmente con le proprietà di simmetria RR’’ = perimetro(RMQ) e similarmente NN’’ = perimetro (NPQ).
Cioè il triangolo RMQ è quello di perimetro minimo tra tutti quelli costruiti con le “riflessioni” opportune partendo da un punto N qualsiasi.
[Per quanto visto nel messaggio precedente per ogni punto N il triangolo costruito con le opportune “riflessioni” ha perimetro minore di qualsiasi triangolo inscritto in ABC che abbia vertice in N.]
Sia N un punto sul lato BC del triangolo ABC. Costruiamo un triangolo con un vertice in N e gli altri due su AB e AC, E e D rispettivamente in modo tale che <NDC = <ADE e <AED = <NEB.
Questo si ottiene determinando N’ simmetrico di N rispetto ad AB ed N’’ simmetrico di N’ rispetto ad AC.
D è l’intersezione di NN’ e AC, mentre E è l’intersezione di DN’ ed AB.
Sia NRS un triangolo con R su AB ed S su AC. Se R’ è il simmetrico di R rispetto ad AC, si ha che SR = SR’ e RN = RN’ = R’N’’.
Quindi il perimetro del triangolo NRS è uguale alla spezzata NSR’R’.
Similmente si prova che il perimetro di NED è uguale al segmento NR’’.
Evidentemente NR’’ è minore di qualsiasi spezzata che congiunge N ed R’’.
In questo modo si è provato che dato un qualsiasi triangolo con vertice in N, possiamo determinarne uno per N che ha perimetro minore.
Avendo provato (con riferimento alla figura 2) che il minore dei triangoli NED è quello per cui N è il piede dell’altezza da A, si può concludere che il triangolo con i vertici sui piedi delle altezze è quello di perimetro minimo tra i triangoli inscritti.
Gentilissimo, ha ragione, sono stato un po' sintetico.
Cercherò di dimostrare l'asserto.
Come detto il percorso QRP è chiuso e deve essere minimo.
Pertanto, come ben noto, gli angoli di incidenza e di riflessione (ed i complementari) devono essere uguali.
La dimostrazione a ciò è fornita dal Teorema di Erone.
***
I 3 triangoli esterni (APQ, QCR ed RBP) devono essere necessariamente simili.
Per dimostrare la similitudine si osservi la figura.
Risulta:
Dal triangolo AQP : β1 = π - α - γ1
dal triangolo QCR : β1 = π - γ - α1
uguagliando le precedenti si ha :
(1) α + γ1 = γ + α1
Dal triangolo RBP : α1 = π - γ1 - β
Sostituendo la precedente nella (1) si ha :
α + γ1 = γ + (π - γ1 - β)
e sviluppando:
α + β + (2γ1 - γ) = π
E' ovvio dunque che
γ1 = γ
e quindi a rotazione:
α1 = α
β1 = β
I 3 triangoli esterni (APQ, QCR ed RBP) sono dunque simili (tra loro e con il triangolo di partenza).
***
Orbene, le normali in P, in Q ed in R sono bisettrici dei loro rispettivi angoli. Credo che non vi siano dubbi al proposito. Ad esempio la normale al lato AC in Q suddivide l'angolo PQR in due parti ognuna pari al complemento di β.
Ma tra le infinite normali passanti per i generici e non ancora definiti punti P, Q ed R posti su AC, CB ed AB, quelle che definiscono il triangolo cercato sono le altezze condotte dai vertici che si oppongono?
Ebbene sì.
I vertici P, Q, R del triangolo cercato sono posti sui piedi delle altezze del triangolo di partenza.
Per dimostrarlo è necessario un semplicissimo e breve ragionamento.
Supponiamo che R sia il piede dell'altezza condotta dal vertice A e consideriamo ad esempio la normale in Q. Se passa per B (ed è quindi l'altezza) deve risultare:
(2) CQ = a cos(γ)
Dalla similitudine tra i triangoli QCR ed ABC risulta:
CQ = c/b CR
Considerando il triangolo ACR risulta:
(3) CR = b cos(γ)
sostituendo nella precedente:
CQ = a cos(γ)
come la (2).
Analogamente può procedersi per P che è posto alla base dell'altezza condotta da C.
Bye
cari amici,
apprezzo i vostri sforzi e ve ne sono grato. Tuttavia, non è facile saltare di commento in commento, per cui pubblico una soluzione più o meno alternativa che permetta di seguire passo dopo passo la dimostrazione... Come avete potuto vedere vi sono molteplici linee d'azione. Io penso di pubblicare la più semplice...