Proseguiamo nella nostra ricerca delle circonferenze tangenti a due circonferenze c1 e c2 che siano esterne tra di loro.

1b. Circonferenze ii

Il procedimento da seguire potrebbe essere nuovamente quello di  modificare della stessa quantità il diametro di c1 e c2, ottenendo circonferenze ausiliarie. Tuttavia, ormai sappiamo che quest'azione non è altro che tagliare i due coni con un piano parallelo al piano xy, anche se in maniera diversa da quanto fatto nel caso ee. Conviene, quindi, guardare il tutto proiettato nel piano xz, come fatto nella Fig. 3. L'unica differenza rispetto a quella figura è la direzione verso cui far scorrere il piano parallelo a xy. Nel caso ee eravamo saliti (aumentando, perciò, entrambi i diametri), questa volta, invece, scorriamo verso il basso, come mostra la Fig.5.

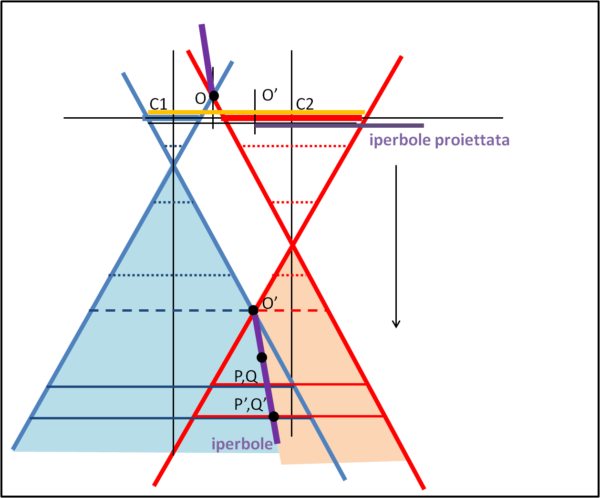
I due coni sono posti esattamente come in Fig. 3 e ciò che cambia sono le loro intersezione con i piani paralleli a xy. La manovra fa decresce il diametro di entrambe le circonferenze ausiliarie che, per tale motivo, non possono avere punti di intersezione (segmenti azzurri e rossi puntinati). A un certo punto la circonferenza azzurra ausiliaria si riduce a un punto, dopo di che inizia ad aumentare di diametro. Quella rossa impiega più tempo ad annullarsi  per potere, poi,  iniziare ad aumentare anche lei. Finalmente possono intersecarsi, iniziando dal momento in cui le due circonferenze ausiliarie sono tangenti tra loro (segmenti azzurri e rossi tratteggiati). Il punto di tangenza O' è il primo centro che abbiamo trovato per il tipo ii. Esso viene proiettato sul piano xy proprio dove si trova il centro della circonferenza "immediata" rossa di Fig. 1. Da questo momento in poi, le circonferenze ausiliarie aumentano entrambe di una stessa quantità (andando verso il basso) e le loro intersezioni danno luogo ai punti P e Q, P' e Q', ecc., come nel caso ee.

La Fig. 6 è del tutto simile alla Fig. 2 e mostra le intersezioni P e Q, P' e Q' proiettate sul piano xy.

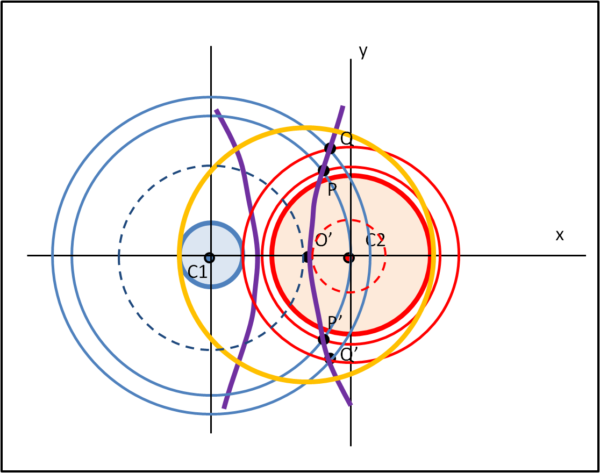
La curva che collega questi punti è, ovviamente, il luogo dei centri delle circonferenze tangenti, di tipo ii,  a c1 e c2. Nella figura è stata anche riportato il ramo d'iperbole relativo al caso precedente ee (a sinistra) e la circonferenza arancione che è quella relativa alla configurazione "immediata" della circonferenza avente centro in O'. Non ci dobbiamo certo stupire della perfetta simmetria, dato che abbiamo, in pratica, descritto la seconda intersezione dei due coni di partenza. Una rozza figura tridimensionale (Fig. 7) mostra quanto fatto finora.

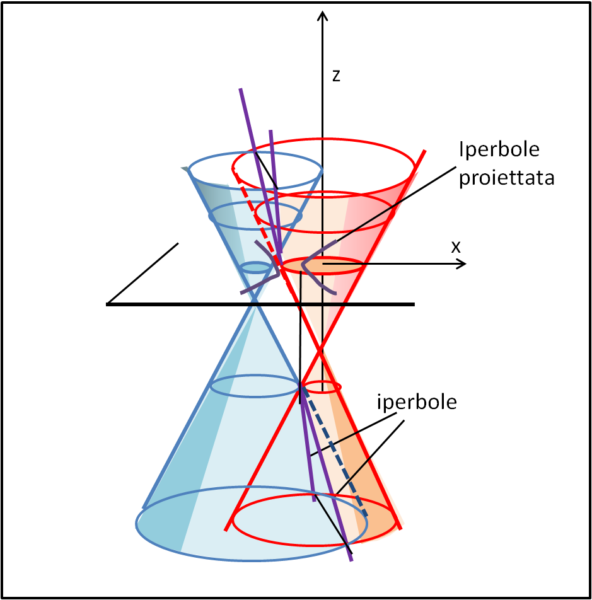
In realtà, le intersezioni dei due coni sono rami di iperboli e stanno tutte su uno stesso piano. Per essere sicuri di ciò possiamo fare un rapido calcolo analitico: le due equazioni dei coni hanno gli stessi termini in x², y² e z², che si elidono cercando l'intersezione. Ciò che rimane è l'equazione di un piano, contenente solo termini di primo grado in x, y e z. Sappiamo inoltre (e Apollonio ce lo insegna) che la proiezione di un'iperbole su un altro piano rimane un'iperbole e questo dimostra chiaramente che le due curve viola di Fig. 6 sono proprio iperboli.

A questo punto possiamo già concludere qualcosa di importante, anche se solo in relazione a due casi particolari. Sul piano xy di Fig. 8, inseriamo le nostre due circonferenze esterne c1 e c2.

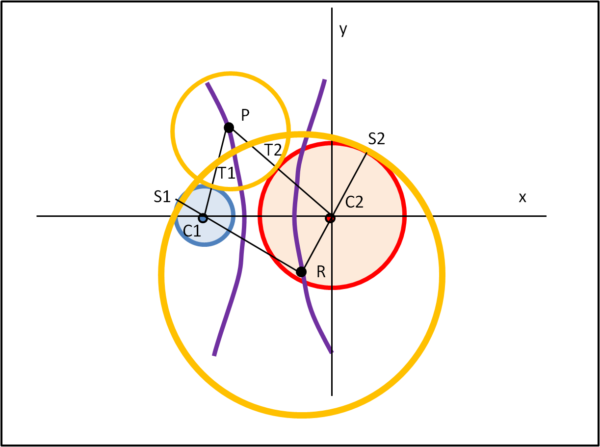
Tracciamo poi le due iperboli che siamo riusciti a costruire attraverso l'intersezione dei coni. Bene, basta scegliere un punto qualsiasi di queste iperboli e tracciare il segmento che lo unisce ai centri di c1 e c2. Nel caso di P, i punti T1 e T2 sono le intersezioni di questi segmenti con c1 e c2. E' immediato fare centro in P e raggio pari a PT1 (o PT2, che deve avere lo stesso valore) per ottenere una circonferenza  arancione del tipo ee tangente  alle due iniziali.  Se prendiamo un punto R sull'altro ramo di iperbole dobbiamo unire R con C1 e C2 e proseguire fino a incontrare c1 e c2 in S1 e S2. La circonferenza arancione di centro R e raggio RS1 (o RS2) ci regala una circonferenza ii tangente alle due iniziali. In altre parole, il ramo di sinistra è relativo alle ee e quello di destra alle ii.

Concludendo, la Fig. 8 permette di descrivere con il solo compasso tutte le circonferenze tangenti di tipo ee e ii.

1c.  Circonferenze ie ed ei

Per ottenere questo nuovo tipo di curve luogo dei centri delle circonferenze tangenti a c1 e c2, dobbiamo "ribaltare" il cono rosso, rispetto al piano xy, ottenendo la Fig. 9.

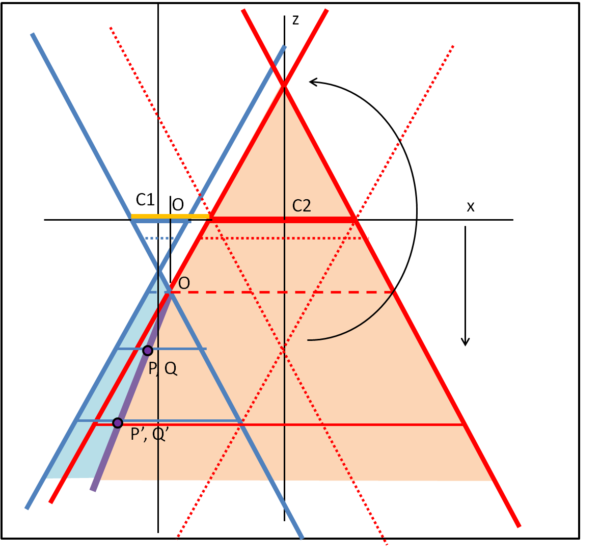
Il cono rosso precedente è quello puntinato, mentre quello nuovo ha i contorni spessi continui. Il centro di c1 rimane ovviamente lo stesso. Non ci resta che fare la solita manovra con un piano parallelo a xy e tagliare i due nuovi coni. Iniziamo andando verso il basso. I segmenti orizzontali puntinati non hanno intersezioni. La prima si ottiene in corrispondenza dei segmenti tratteggiati. Il punto O così trovato è il primo punto che corrisponde al centro della circonferenza immediata del tipo ie. Continuando a scendere otteniamo circonferenze ausiliarie che hanno intersezioni, le cui proiezioni su xy descrivono il luogo dei centri delle circonferenze ie.

La Fig. 10 mostra quanto fatto proiettato nel piano xy, con i nuovi punti P,Q, P',Q', ecc. che sono proprio le proiezioni cercate. Le circonferenze arancioni sono quelle relative ai punti O (caso immediato) e Q.

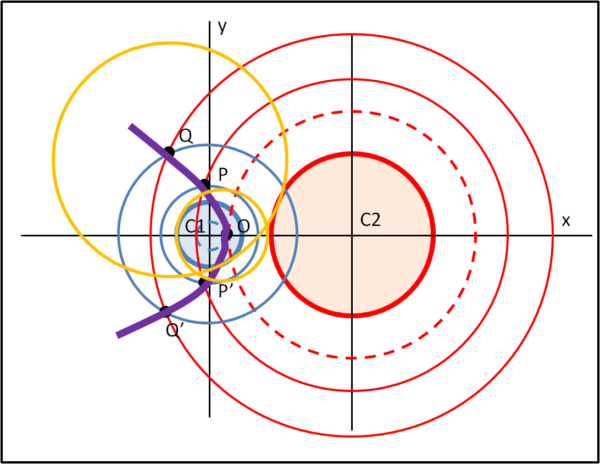
Non ci dobbiamo certo stupire se otteniamo nuovamente un ramo di iperbole, anche se più "schiacciata", dato che abbiamo nuovamente fatto intersecare due coni.

E' ormai ovvia l'azione da compiere per determinare  i centri delle circonferenze ei. Basta infatti tagliare i coni andando verso l'alto, come mostra la Fig. 11.

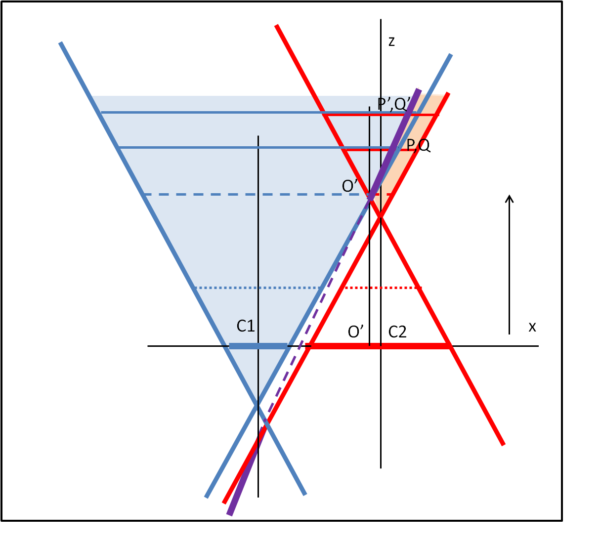
Troviamo prima le circonferenze ausiliarie puntinate (senza intersezioni), poi quelle tratteggiate che individuano O' e infine quelle intersecantesi che determinano P e P', Q e Q', ecc., ossia il luogo dei centri cercato.

La Fig. 12 mostra il tutto proiettato nel piano xy con il nuovo ramo di iperbole (a destra)

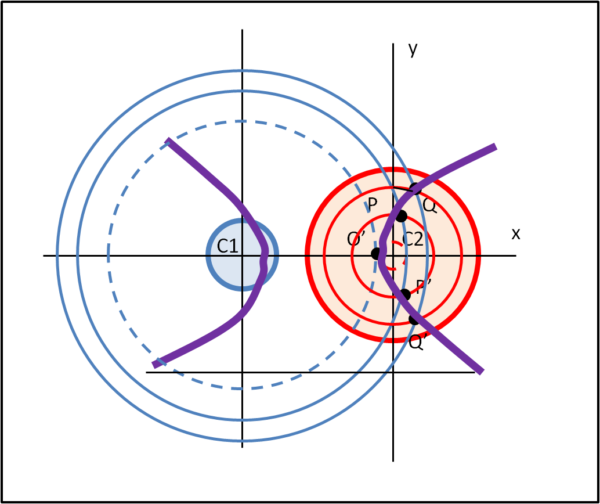
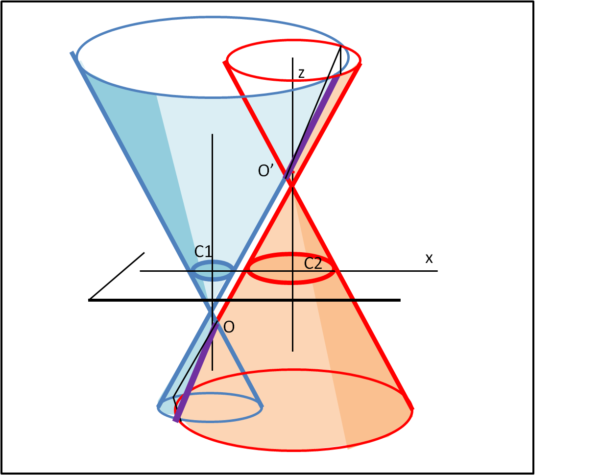
La Fig. 13 mostra lo schizzo tridimensionale relativo alle intersezioni dei due coni, che determinano gli ultimi due rami d'iperbole.

Come conclusione di questa seconda parte, ecco in Fig. 14 tutti i 4 rami di iperbole, proiettati nel piano xy, in grado di regalarci tutti i centri delle circonferenze  del tipo ee, ii, ie ed ei, relativi a due circonferenze c1 e c2 esterne tra loro. Sono anche riportate quattro circonferenze arancioni che rispondono a quanto cercato.

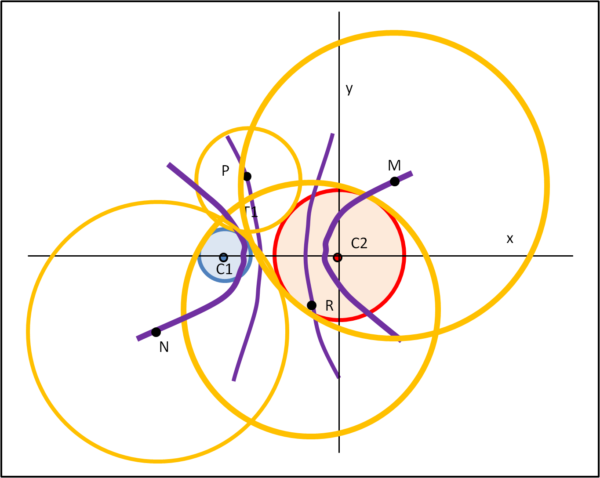
Questa figura è il riassunto di tutto quanto fatto finora e sarà uno strumento fondamentale per il passaggio alle tre circonferenze di partenza, quelle relative al Problema di Apollonio. Tuttavia, prima di fare questo passaggio decisivo, dobbiamo ancora trattare i casi delle due circonferenze c1 e c2 che siano una interna all'altra e intersecantesi tra di loro.

Ormai non dovrebbe più essere difficile il procedimento, ma per essere didattici fino in fondo lo tratteremo con la dovuta attenzione. Due coni sanno fare meraviglie!