E' un po' che stiamo proponendo argomenti di geometria non sempre banali. Che ne dite di tornare alla fisica classica? Bene, questo è un quiz, accompagnato dalla soluzione, che mi sembra particolarmente interessante per capire al meglio i moti relativi. Argomento, questo, elementare, ma che, a volte, può creare qualche confusione. Il quiz è sicuramente semplice, ma sicuramente molto didattico. Ne approfittiamo per rinfrescare concetti assunti troppo spesso come ovvi, relativi a vettori, velocità e distanze.

Quiz

Il problema è stato proposto all'Università di Manchester. La soluzione "ufficiale", però, benché corretta, sembra piuttosto laboriosa e inutilmente complicata nella sua seconda parte.  In particolare, non utilizza il risultato della prima parte per arrivare velocemente e -più elegantemente- alla soluzione finale. Proponiamo, perciò, sia la strategia ufficiale sia quella che è sicuramente più elegante e rapida.

Due navi (A e B) stanno viaggiando in mare aperto. A si dirige verso Nord con una velocità di 30 km/h, mentre B, che si trova a 10 km a Est di A (al tempo t = 0), viaggia a soli 20 km/h lungo una direzione che forma un angolo di 60° con la direzione del Nord.

Le domande sono due:

(1) Determinare modulo e velocità della nave B rispetto alla nave A.

(2) Determinare la loro distanza al momento del massimo avvicinamento e il tempo impiegato per raggiungere questa configurazione.

Il quiz è aperto a tutti, ma sicuramente lo affronteranno i soliti esperti del Circolo. Non ho, quindi, problemi a riportare di seguito anche le soluzioni, dato che sono sicuro che non sarà letta da chi ha la volontà, la capacità  e il "coraggio" di rispondere.

Velocità relativa.

a) Introduzione elementare *

Potremmo parlare subito di vettori, ma approfittiamone per richiamare i concetti legati alle velocità relative in ambito galileiano. Non trattandosi di relatività ristretta, ammettiamo che il tempo sia uguale per ogni sistema di riferimento. Ciò vuole dire che possiamo trattare le velocità come spazi divisi per un tempo, uguale per tutti. Parlare di velocità vuol quindi dire parlare di spazi percorsi nell'unità di tempo, ad esempio l'ora.

Consideriamo, in Fig. 1, un sistema di coordinate x,y e poniamo due punti A e B nell'origine O degli assi.

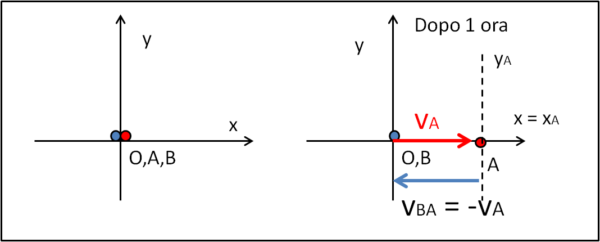
Come caso più banale, facciamo muovere A con velocità costante v_A lungo l'asse x, mentre B sta fermo.  Quale è la velocità di B relativa ad A? Ossia, a che velocità (v_BA) A vede muovere il punto B ? Il tutto si riduce a considerare A fermo e determinare la velocità di B nel sistema di riferimento solidale con A.

La soluzione è veramente immediata. A, nel suo sistema di riferimento tratteggiato (l'asse delle x rimane inalterato) che continua ad avere l'origine in A, vede B che si allontana da lui, nella direzione negativa dell'asse x.  Più esattamente B sembra muoversi con una velocità uguale e contraria a quella che A ha rispetto all'origine O. In altre parole, in un certo tempo t (poniamolo uguale a un'ora) il punto B si è allontanato di v_A km. Più esattamente di - v_A. Possiamo scrivere:

v_BA = - v_A

Ripetiamo... abbiamo indicato dei semplici segmenti con il simbolo v delle velocità in quanto stiamo considerando un tempo uguale all'unità di tempo. Ossia: v = s/t = s/1 = s.

Cambiamo leggermente la situazione e facciamo muovere anche B, nella stessa direzione di A ma con una velocità minore, v_B. Dopo un'ora la situazione è quella di Fig. 2.

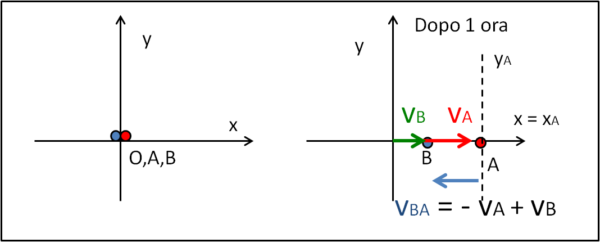
Come viene visto B da A? Facile... B si allontana come prima, ma cerca di stare dietro ad A andando nella stessa direzione. A vede B perdere meno terreno. Dopo un'ora la distanza tra A e B è uguale alla distanza di A rispetto ad O, meno la distanza di B rispetto ad O. Passando alle velocità (basta dividere le distanze per il tempo trascorso, che è unitario) possiamo scrivere che la velocità v_BA (di B rispetto ad A) è proprio

v_BA = - v_A + v_B

Questa differenza è negativa dato che vA è maggiore in valore assoluto di v_B. Ovviamente, potremmo anche dire che la velocità di A rispetto a B ha lo stesso valore assoluto, ma con il segno cambiato. In altre parole B vede  allontanarsi A con la stessa velocità misurata da A, ma inverso opposto. ossia:

v_AB = - v_BA

Bene, passiamo al caso più generale di Fig. 3.

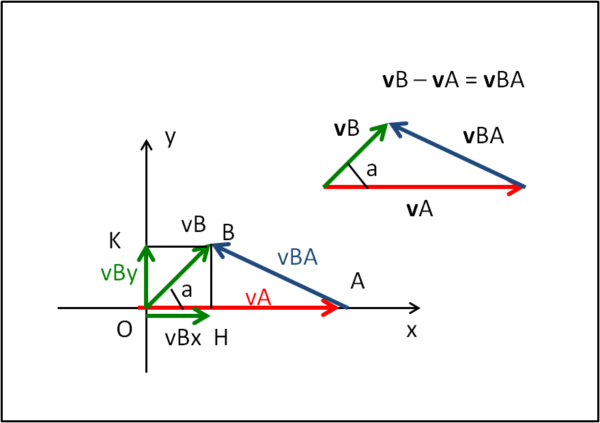
A si muove con velocità v_A verso destra. B si muove  con velocità v_B in direzione inclinata di un angolo a rispetto all'asse delle x

Cosa vede A? Possiamo scomporre il "segmento" v_B nelle sue due proiezioni su x e y e chiamarle v_Bx e v_By. 

Seguiamo il procedimento più lungo ed elementare, ricordando un minimo di trigonometria. Iniziamo da ciò che vede A lungo l'asse x. Tutto è uguale al secondo caso appena trattato, considerando solo la componente v_Bx.

v_BAx = - v_A + v_Bx                  .... (1)

Rimane la componente vBy. A non ha componente di velocità lungo y, per cui, secondo il  sistema di riferimento di A, B si muove lungo y' verso l'alto:

v_BAy = 0 + v_{By                        .... (2)}

Possiamo concludere che il modulo della velocità di B rispetto ad A è proprio dato dal segmento AB.

Dal triangolo rettangolo BHA è facile ottenere la lunghezza del segmento AB, ossia il modulo della velocità v_BA 

v_BA² = v_BAx² + v_BAy²            .... (3)

Inserendo la (1) e la (2) nella (3) otteniamo:

v_BA² = (- v_A + v_Bx)² + v_By²

Usiamo la più elementare trigonometria per scrivere v_Bx e v_By in funzione di v_B e dell'angolo a.

v_Bx = v_B cos a

v_By = v_B sin a

sostituendo

v_BA² = (- v_A + v_B cos a)² + (v_B sin a)²

v_BA² = v_A² + v_B²cos² a - 2 v_A v_B cos a + v_B sin² a

ricordando che sin² a + cos² a = 1

v_BA² = v_A² + v_B² - 2 v_A v_B cos a                            .... (4)

La formula ottenuta è una relazione ben nota, conosciuta come teorema del coseno o di Carnot. Essa è un classico e potevamo utilizzarla direttamente senza usare Pitagora e le componenti dei vettori, applicandola direttamente al triangolo OBA.

Cercando di essere i più elementari possibile abbiamo allungato un calcolo che sarebbe stato immediato conoscendo questo teorema. Tuttavia, niente di male, dato che così facendo lo abbiamo dimostrato.

b. Calcolo vettoriale.

Finora abbiamo lavorato con segmenti che altro non erano che i moduli delle velocità di A e di B. Potevamo, invece, introdurre direttamente i vettori, ossia le velocità con tanto di modulo, direzione e verso. In altre parole lasciar perdere i sistemi di riferimento e le varie coordinate, ma agire direttamente sulla somma e differenza di vettori, come mostra la Fig. 3, in alto a destra.

In pratica, dati due vettori è facile costruire il parallelogramma che mostra il vettore somma o differenza. Nel nostro caso v_BA risulta essere proprio v_B.- v_A. Il triangolo della figura ci dice che v_BA è il vettore differenza tra vB e vA. Per conoscere il modulo di v_AB, basta applicare il teorema del coseno e scrivere immediatamente la (4). L'angolo a non è altri che l'angolo tra v_B  e  v_A. 

Notiamo che il calcolo della velocità relativa può essere compiuto indipendentemente dagli assi cartesiani.

Vi chiedo di perdonarmi se ho scritto qualcosa di veramente elementare, soprattutto per i lettori del nostro Circolo, ma, come dico spesso, è meglio abbondare...

Soluzione del quiz

(1) velocità relativa e sua direzione **

La prima domanda chiede di calcolare la v_BA, ossia sia il suo modulo che la sua direzione. Possiamo, per questo scopo, trascurare del tutto la posizione relativa delle due navi, ossia i 10 km iniziali. Non stiamo, infatti, parlando di distanza relativa, ma di velocità relativa. La velocità relativa non cambia qualsiasi sia la posizione iniziale delle due navi, contano solo le loro velocità.

Immaginiamo, quindi, che le due navi siano entrambe nella posizione O, origine degli assi, all'istante t = 0. Dopo un'ora ad esempio, A si è portata in A', mentre B si è portata in B'. Le distanze rappresentano perfettamente i moduli delle due velocità, come mostra la Fig. 4.

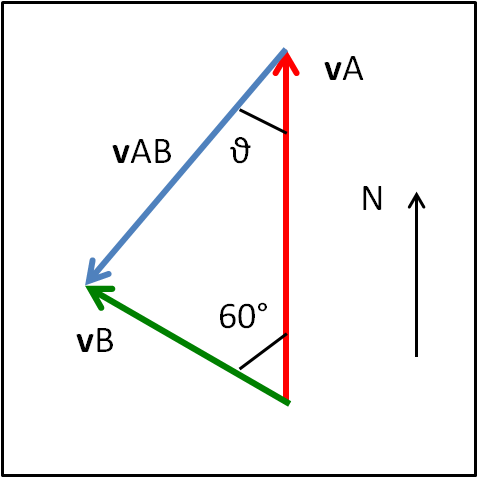
Non abbiamo bisogno di componenti secondo gli assi, per quanto abbiamo imparato precedentemente. Basta indicare i vettori velocità, con le loro lunghezze (note) e calcolare v_BA = - v_A + v_B. L'applicazione diretta del teorema del coseno (che è la (4)) regala la soluzione relativa al modulo di v_AB.

v_BA² = v_A² + v_B² - 2 v_A v_B cos a

v_BA² = 30² + 20² - 2 · 30 · 20 cos 60°

v_BA² = 900 + 400 - 600 = 700

v_BA = √700 = 10√7 ≈ 26.46 km

Non ci resta che determinare la direzione del vettore v_AB. In altre parole, l'angolo θ tra v_AB e la direzione, ad esempio, Sud-Nord (che è poi quella di v_A).

Il modo più semplice per risolvere questa parte del quiz è -probabilmente- l'applicazione del teorema dei seni. Esso dice che il rapporto tra i lati di un triangolo e gli angoli opposti rimane costante. Nel nostro caso:

v_B/sin θ = v_BA/sin 60

Da cui

sin θ = v_B sin 60/v_BA  = 20 · 0.866 /10√7 ≈ 0.655

θ ≈40°.9

(2) distanza tra le navi.

(2)a. Soluzione "ufficiale" dell'Università di Manchester.

Abbiamo visto che nei moti relativi, la velocità relativa dipende solamente dai vettori velocità dei due punti in movimento. Non importa quale sia la loro effettiva posizione dello spazio x,y. La seconda parte del quiz, invece, introduce la distanza tra le due navi. Questa parte è risolta senza bisogno di conoscere la velocità relativa. Tuttavia, mostra un calcolo piuttosto lungo e laborioso e sembra del tutto inutile avendo già a disposizione, dalla prima risposta, modulo e direzione di vBA.

Può essere, comunque, interessante riportarla se non altro per motivi puramente didattici.

La distanza tra le due navi cambia al variare del tempo, in quanto le navi si muovono, ognuna secondo la propria velocità.

La faccenda si risolve, allora, attraverso la Fig. 5

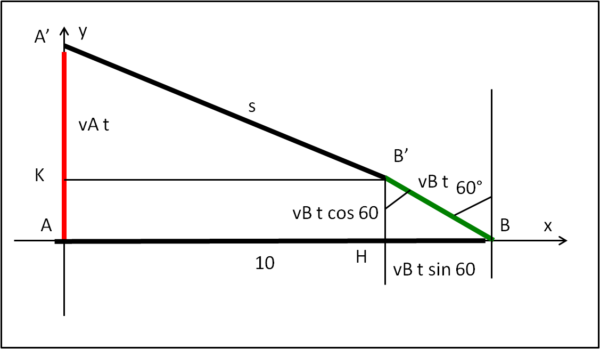
Siamo tornati nel sistema x,y e sappiamo che, al tempo t = 0, A si trova nell'origine e B a 10 km di distanza lungo l'asse x (Est). Facciamo muovere le navi e consideriamo la loro posizione relativa a un tempo t qualsiasi. Ogni nave ha seguito la sua traiettoria muovendosi con la propria velocità. Chiamiamo A' e B' le due navi al tempo t. Vogliamo determinare la distanza s, ossia la lunghezza del segmento A'B'.  Basta, perciò, determinare l'ipotenusa del triangolo rettangolo A'KB'. I suoi cateti sono:

A'K = A'A - KA

Ma sappiamo che  A'A  è la distanza percorsa da A nel tempo t, ossia possiamo scriverlo come velocità moltiplicata per un tempo...

A'A = v_A t

Analogamente KA è data da:

KA = v_B t cos 60

A'K = v_A t - v_B t cos 60

L'altro cateto B'K può essere scritto come:

B'K = AB - HB

Ma

AB = 10

HB = v_B t sin 60

B'K = 10 - v_B t sin 60

Applichiamo Pitagora al triangolo A'KB' e otteniamo s

s² = (v_A t - v_B t cos 60)² + (10 - v_B t sin 60)² .... (5)

s = √((30 - 20 · 0.5)t² + (10 - 20 · 0.866 t)²)

s è una funzione di t. Per trovare il suo valore minimo basta uguagliare a zero la sua derivata prima.

Il valore di t  che corrisponde al minimo valore di s risulta essere:

t = 0.247 h

inserendo t nella (5) otteniamo:

s² = 57.14

s = 7.56 km

2(b). Soluzione del ... Circolo

Il metodo appena descritto è senza dubbio corretto, ma estremamente lungo e laborioso. Conoscendo la velocità delle due navi, abbiamo già ricavato il modulo della velocità relativa v_AB e l'angolo della sua direzione rispetto al Nord. Questo dato ci permette di ricavare la minima distanza (e quanto tempo è passato dall'istante zero)  attraverso un semplice triangolo rettangolo.

Utilizziamo la Fig. 6

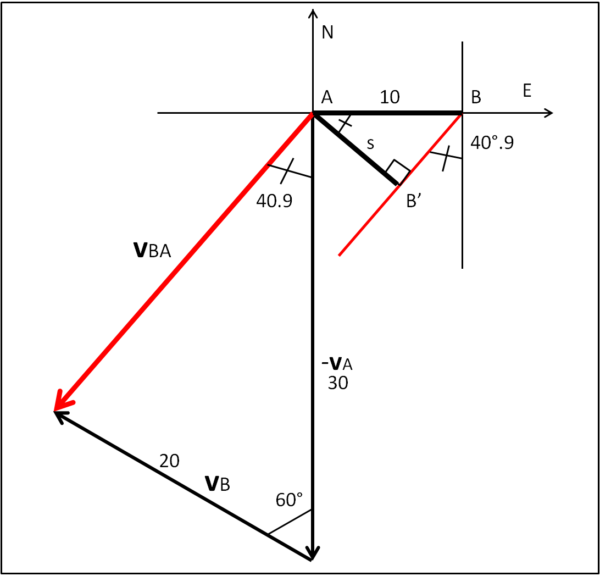
Nella parte sinistra abbiamo riportato i vettori che hanno permesso di determinare modulo e direzione di vAB. Sappiamo, quindi, che A vede B muoversi lungo la direzione di v_AB. Poniamo A nell'origine come punto fisso e facciamo muovere B secondo questa direzione.

Qual è la minima distanza tra un punto e una retta? Facilissimo... E' il segmento perpendicolare alla retta. Tutto si risolve con il triangolo rettangolo ABB'.

s = AB' = AB cos 40.9

s ≈ 7.56 km

Per avere il tempo t, basta ricordare che:

BB' = v_AB t = 10 sin 40°.9

da cui:

t = 0.247 h

Mi spiace per Manchester, ma questa soluzione è decisamente più semplice ed elegante!