Affrontiamo un problema sicuramente conosciuto da tutti e probabilmente anche provato al Luna Park: il giro della morte. Per i più paurosi non è difficile eseguirlo senza rischi attaccando un peso m a un filo inestensibile e facendolo ruotare in senso verticale. In altre parole, un pendolo libero di ruotare attorno a un punto fisso. Un problema, questo, abbastanza semplice che, però, viene, qualche volta , presentato in modo un po' confuso se non addirittura sbagliato. Attenzione, perciò, a ciò che trovate in rete...

In pratica, abbiamo di fronte un moto circolare su un piano verticale, dove la massa m, in rotazione attorno al punto centrale in cui si collega il filo, subisce la forza di gravità. Ne consegue un moto circolare non uniforme, soggetto all'accelerazione di gravità. Vi pongo, perciò, una domanda molto diretta: "E’ vero che le condizioni limite per permettere a una pallina P, di massa m,  appesa a un filo f inestensibile, di compiere il giro della morte attorno ad O, fisso, sono quelle che corrispondono a una velocità uguale a zero nel punto più alto A ?" E' facile rispondere, così come è facile risolvere il problema, ma stiamo bene attenti alle varie condizioni limite perché il giro della morte possa realizzarsi.

Ecco, perciò un problema che utilizza proprio questo tipo di moto, anche se leggermente più complicato. Lo vediamo nello schema di Fig. 1

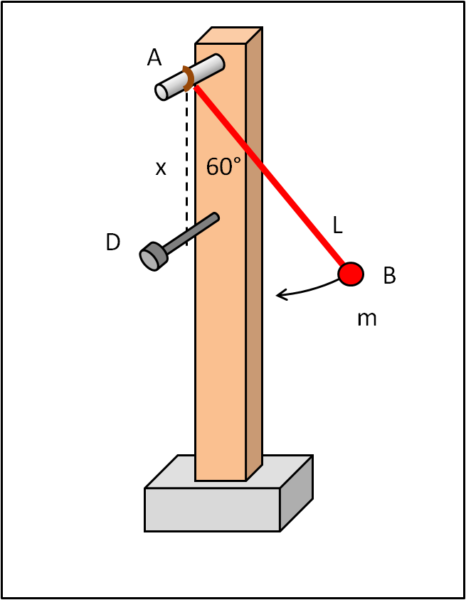
Il filo inestensibile AB di massa trascurabile e lunghezza L ha al suo estremo una sferetta di massa m che viene lasciata libera di "cadere" quando il filo forma un angolo di 60° con la verticale. Sul sostegno del punto A di rotazione viene inserito un chiodo D. Si chiede:

A che distanza x dal punto A deve essere fissato il chiodo D affinché la pallina  riesca a compiere il giro della morte attorno a D? Si chiedono, ovviamente, le condizioni limite perché ciò possa avvenire.

Assumiamo che non vi siano presenti attriti

Spero, come sempre, in qualche risposta, ma so che non arriveranno... Eccovi perciò la soluzione.

SOLUZIONE

Cominciamo con lo studio del moto della pallina che parte da B e, in particolare, siamo interessati alla velocità che essa raggiunge nel punto C, esattamente sulla verticale passante per A (Fig. 2).

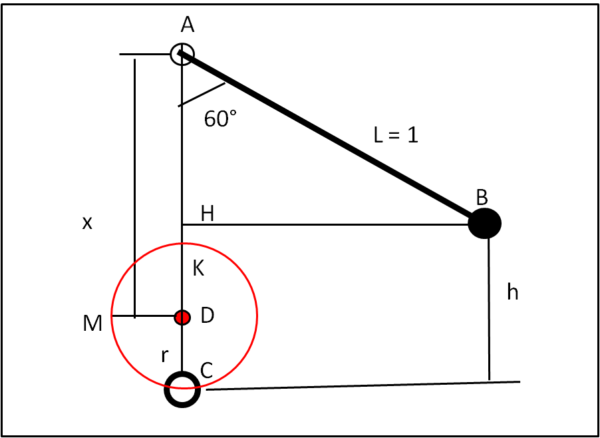
Sappiamo che la pallina parte da ferma e, quindi, non è certo difficile uguagliare l'energia meccanica in B e quella in C, sapendo benissimo che essa deve conservarsi. Scriviamo:

Ek(B) + Ep(B) = Ek(C) + Ep(C)

Dove Ek e Ep sono rispettivamente l'energia cinetica e quella potenziale. Dovendo trattare un fenomeno che avviene nei pressi della superficie terrestre possiamo considerare l'accelerazione g come una costante e porre uguale a zero l'energia potenziale in C. Ricordiamo che trattando con l'energia potenziale quello che conta è la differenza di energia tra un punto e un altro e lo zero può essere assunto dovunque.

La pallina parte da ferma , perciò v_B = 0

Ek(B) = 1/2 m v_B² = 0

Ricaviamo l'altezza h della pallina in funzione di L, posto uguale a 1.

AH = L cos 60° = L/2 = 1/2

h = AC - AH = 1 - 1/2 = 1/2

L'energia potenziale in B è:

Ep(B) = hmg =  mg/2

La Ep(C) deve essere uguale a zero, per come lo abbiamo scelto, mentre Ek(C) assume un valore legato alla velocità v_C, raggiunta dalla pallina nel punto più basso.

Ne segue che la conservazione dell'energia porta alla seguente espressione:

E(B) = Ek(B) + Ep(B) = 0 + mg/2

E(C) =Ek(C) + Ep(C) =

0 + mg/2 =  1/2 mv²_C + 0

v_C = √g

La prima parte dell'esercizio è finita, avendo calcolato la velocità nel punto più basso della pallina. Quando si raggiunge questa situazione, ecco, però, che il filo incontra il chiodo D che diventa il centro della nuova rotazione della pallina. Il raggio di questo moto circolare è adesso r (r = DC) e ciò che vogliamo è che la pallina riesca a fare il giro della morte, ossia riesca a raggiungere il punto K.  Conosciamo, però, la velocità (v_C) con cui viene affrontato. Tale velocità è quella che decide se il raggio DC possa essere affrontato evitando una caduta. Vogliamo le condizioni limite per cui questo capiti. Ragionando senza numeri è facile concludere che maggiore è la velocità v_C e più in alto la pallina riesce ad arrivare senza cadere prima della posizione critica K. Quest'ultima è, quindi, la posizione da analizzare, essendo il momento fondamentale dell'intero problema.

Ragioniamo ponendoci nel sistema di riferimento della pallina. Quando essa arriva in K deve essere nelle condizioni in cui la forza centrifuga eguaglia perfettamente quella di gravità. In altre parole, essa deve raggiungere le condizioni di perdita di peso. Potrebbe avere velocità uguale a zero? Assolutamente NO, dato che se la velocità fosse zero, sarebbe zero anche la forza centrifuga e la pallina sarebbe soggetta solo alla forza peso. Ricordiamo, infatti, che l'accelerazione centrifuga vale:

a_cf = v²/r              .... (1)

Non commettiamo, perciò, l'errore di accettare una velocità nulla in K. Essa non potrebbe mai essere raggiunta, dato che la pallina cadrebbe molto prima. Compiendo il tentativo di effettuare il giro della morte, la velocità della pallina non solo cambia sempre direzione, come in tutti i moti circolari uniformi, ma cambia anche il modulo dato che la gravità tende a rallentarla. Se la v_C è troppo bassa la pallina non riesce nemmeno a giungere in M ed è costretta a tornare indietro lungo la traiettoria circolare appena eseguita. Se è abbastanza alta riesce ad arrivare in M con una certa velocità, ma non certo sufficiente a controbilanciare la gravità: la pallina si inserisce in una traiettoria parabolica e il filo smette di essere teso. Per potere arrivare in K deve perciò avere ancora una certa velocità, proprio quella che le permette di continuare il moto circolare e tornare in C continuando nel suo moto circolare non uniforme..

La relazione (1) ci dice qual è la velocità minima che si deve raggiungere:

v²_min /r = g

In altre parole: la accelerazione centrifuga deve essere uguale a quella peso, in modo che la pallina rimanga praticamente sospesa, ma con una certa velocità che vale proprio:

v_min = √(gr)

Non ci resta che legare questa velocità minima richiesta alla velocità che la pallina ha in C, quando inizia la "salita" attorno al chiodo. Utilizziamo nuovamente la conservazione dell'energia. In C l'energia potenziale è zero, mentre quella cinetica vale 1/2mv_C². Quando la pallina arriva in K, l'energia cinetica vale 1/2mv²_min, mentre quella potenziale vale 2rmg, dato che l'altezza raggiunta vale proprio due volte il raggio del giro della morte...

1/2mv_c² = 1/2mv²_min + 2mgr

moltiplicando tutto per 2 e semplificando la massa m

v_C² = v²_min + 4 gr

Sostituiamo i valori appena trovati

g = gr + 4 gr

g = 5gr

r = 1/5

x = 1 - r = 1 - 1/5 = 4/5 = 0.8

Ricordiamo, soprattutto, il valore della velocità da impartire in C per ottenere il giro della morte di raggio r:

v_C = √(5gr)

ossia deve essere √5 volte il valore della velocità nel punto più alto, dove vale √gr.