Soluzione del "banale" esponente **
Il problema è più semplice di quanto si possa pensare a prima vista. In pratica ci dice di risolvere questa equazione:
(x2 - 7x + 11)(x² - 11x + 30 ) = 1
Un metodo abbastanza rapido sarebbe quello di eseguire il grafico della funzione di sinistra e vedere dove taglia l'asse y = 1, come mostrato nella Fig. 1.
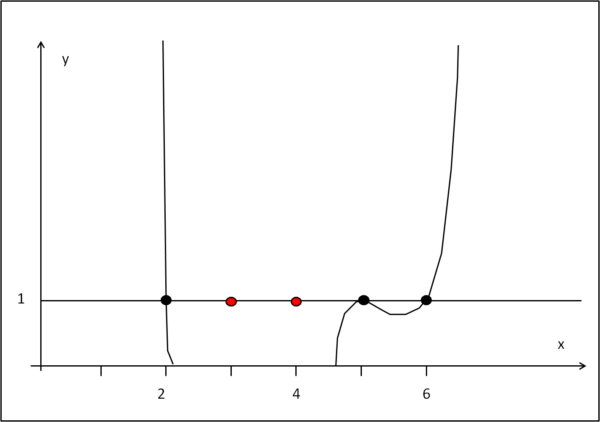
I punti sembrerebbero tre, e le ascisse corrispondenti sarebbero 2, 5 e 6.
Tuttavia, non sempre basta l'occhio. A volte è necessario "scovare" soluzioni nascoste.
Agiamo, perciò, in modo algebrico. Come possiamo fa sì che la parte di sinistra sia uguale a 1? Vi sono, ovviamente, due modi: porre uguale a 1 la base oppure porre uguale a zero l'esponente. In altre parole:
1k = 1
k0 = 1
Nel secondo caso è necessario, però, che k sia diverso da zero, altrimenti avremmo una forma indeterminata.
Queste semplici relazioni ci permettono di trovare facilmente le soluzioni. Basta, infatti, porre uguale a 1 la base (x2 - 7x + 11) e porre uguale a 0 l'esponente (x² - 11x + 30 )
Niente di più facile, trattandosi di semplici equazioni di secondo grado in x. La prima ci fornisce i valori
x = 2
x = 5
La seconda equazione ci regala:
x = 5
x = 6
Prima di accettarle, però, dobbiamo essere sicuri che la base sia diversa da zero. Bene, basta inserire questi valori nella base e verificare che essa sia diversa da zero. Così è, infatti, per cui le soluzioni sono valide.
Tutto risolto? Sembrerebbe di sì, anche perché quanto ottenuto coincide perfettamente con il grafico. E, invece, no... stiamo perdendo due soluzioni davvero "singolari". Vi è, infatti, un altro modo per ottenere il nostro risultato di 1.
(-1)2k = 1
In altre parole, dobbiamo porre uguale a -1 la base e verificare che l'esponente sia un numero intero pari.
La base posta uguale a -1 ci regala due nuove soluzioni:
x = 3
x = 4
Verifichiamo che l'esponente sia un numero pari intero inserendo nell'esponente i valori di x appena trovati. Otteniamo i valori di 6 e di 2, che sono interi positivi. Si può concludere che anche le ultime due soluzioni sono valide. Nella Fig. 1 dobbiamo perciò aggiungere due soluzioni, segnate in rosso. La funzione non appare nel grafico perché in quella regione assume solo valori complessi, tranne che in quei due punti.
4 commenti
caro Fabry,
hai toccato un argomento molto delicato. Non tutte le operazioni che si fanno con i numeri reali possono essere trasferite ai numeri complessi... Ricordiamoci, ad esempio, che
√-1 √-1 non vale √(-1)(-1) che sembrerebbe portare a √1 = 1. Infatti...
-1 = i2 = √-1 √-1 = 1
Un bel paradosso, direi...
Tra parentesi
i2 = -1 implica che la radice quadrata abbia SEMPRE due soluzioni:
i = +/- √-1
i2 = -1 è la definizione esatta di i, mentre considerare
i = √-1
vuol dire trascurare una radice e considerare solo quella principale.
Non è banale andare a fondo della questione, dato che non vi è nemmeno accordo tra i matematici... Tuttavia, mi hai dato lo spunto per parlare un po' di operazioni "semplici" complesse.
Grazie, come sempre, per i tuoi commenti!
La questione sollevata è molto interessante, perché coinvolge l’insieme dei numeri complessi che, sotto alcuni aspetti, risulta abbastanza .... “complesso”.
Probabilmente “l’inghippo” sta nel fatto che – come ricordava giustamente Enzo – non sempre le operazioni nel campo dei numeri reali possono essere “trasportate” in maniera del tutto equivalente al campo dei numeri complessi.
Difatti, la potenza esaminata:
Ora, la radice cubica di −1 deve restituire, nel campo dei numeri complessi, un numero di soluzioni pari all’indice della radice:
Ma dall’identità di Eulero abbiamo che:
Elevando al quadrato le ultime 2, queste non restituiscono 1.
Quindi delle tre soluzioni della radice cubica, solo quella di parte reale −1 , successivamente elevata al quadrato, da come risultato 1.
dici bene, caro Andy...
Spesso si trascurano alcune o molte soluzioni. Tra poco ne farò un classico esempio... Ricordiamoci sempre che i numeri complessi si ottengono facendo ruotare un vettore nel piano complesso. Passare da forma algebrica a trigonometrica o esponenziale comporta non poche sorprese. Sarebbe molto interessante studiare anche come sono nati i numeri negativi, argomento veramente critico in occidente (ma non in oriente).