A volte vengono chiamati numeri catalani, ma niente hanno a che vedere con la Catalogna e i suoi abitanti!

Conosciamo bene alcune serie numeriche famose e di larghissimo uso. Ad esempio la serie dei quadrati dei numeri interi

1, 4, 9, 16, 25, 36, ...

O, ancora, le serie che corrispondono ai multipli di un numero intero. Per 2, ad esempio, abbiamo

2, 4, 6, 8, 10, 12, 14, ...

Queste sono, ovviamente, molto semplici e ogni numero che le forma è facilmente calcolabile. Ve ne sono, però, di altrettanto celebri che corrispondono a calcoli un po' più complessi. Esempio straordinario è la serie di Fibonacci

0, 1, 1, 2, 3, 5, 8, 13, 21, ...

il cui il termine Fn è uguale alla somma dei due termini precedenti (F_n-1 + F_n-2). Sappiamo bene quante applicazioni ha in un'infinità di situazioni non solo scientifiche.

Molto meno conosciuta, ma decisamente altrettanto utilizzata è la serie dei numeri di Catalan.

Scriviamola:

1, 1, 2, 5, 14, 42, 132, 1430, 4862, 16796, ...

Beh... sicuramente è molto meno intuitiva tant'é che il sommo Eulero (colui che l'ha pensata) ha avuto problemi a trovarne il termine generico. In realtà la relazione risolvente fu trovata nel 1838 dal matematico belga Eugene Catalan, mentre studiava il problema delle parentesi (ne parleremo in seguito). Dato che si deve praticamente a lui se è stata, in qualche modo, riscoperta e ha mostrato le sue numerosissime applicazioni odierne, si è scelto di darle il suo nome (Eulero aveva già a suo nome di tutto e di più...).

Torniamo ad Eulero. Il suo era un problema essenzialmente geometrico. Ossia: "Trovare tulle le possibili triangolazioni di un poligono convesso di n lati utilizzando tutti i vertici ed escludendo le intersezioni tra linee". Per capire esattamente il problema, è meglio utilizzare un disegno... consideriamo, ad esempio, il pentagono, in Fig. 1.

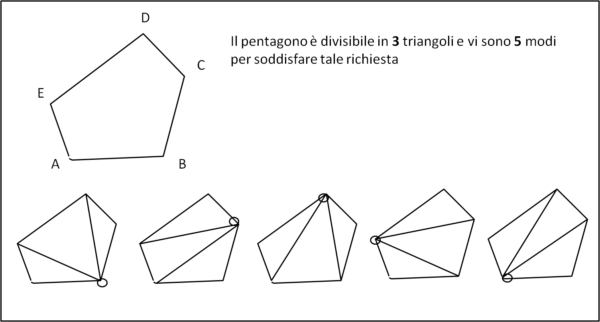
Abbiamo ottenuto il numero 5, ossia esistono 5 modi possibili  per dividere la figura di partenza in un certo numero di triangoli. Questo termine corrisponde al numero C3, ossia a n - 2 triangoli. Attenzione! Non vogliamo il numero di triangoli, che sarà sempre pari a n - 2, ma il numero di possibili combinazioni, che per n = 5 sono proprio 5.

Eseguiamo il calcolo anche per i quadrilateri. Essi corrispondono a C2 (n - 2 triangoli) e danno come risultato il numero 2. Vi sono solo due modi per suddividerlo in triangoli. Possiamo anche considerare il triangolo. Ovviamente, in questo caso esiste un solo triangolo, quello di partenza, e solo un modo per suddividerlo in triangoli. Ne segue che C₁ = 1. Si pone anche, per convenienza, C₀ = 1.

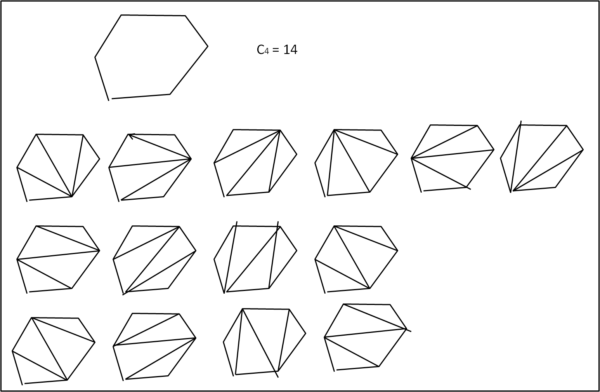
Per entrare ancora meglio nella problematica di Eulero, proviamo a passare all'esagono, come mostra la Fig. 2. Si ottengono ben 14 possibili divisioni. Ossia C4 = 14.

Il nostro Eulero si spinse fino al calcolo relativo a n = 8 (ossia al decagono), ma si deve al suo collega e amico Johann Andreas von Segner la definizione di una formula ricorrente in grado di trovare l'ennesimo termine della successione, conoscendo quelli precedenti. Un primo passo, ma ancora piuttosto faticoso, dato che presupponeva la conoscenza di Cn-1, Cn-2, ...., Co. La formula è la seguente:

Cn = ∑_i=0^n-1 C_i C_{n-1 - i}

Imponendo C0 = 1

In notazione meno compatta

C_n = C₀C_n-1 + C₁C_n−2 + C₂C_n−3 + . . . + C_n-1C₀ .

Von Segner calcolò i valori per n ≤ 18, nel suo articolo "Enumeratio modorum, quibus figurae planae rectilineae per diagonales dividuntur in triangula" del 1758/59, ma commise un errore nel calcolo di C₁₃ che rese inutili i risultati seguenti.

La formula è dimostrabile in modo abbastanza semplice e vediamo di spiegare come ci si arriva. Ricordiamo, ancora, che non vogliamo sapere il numero dei triangoli ma il numero delle divisioni possibili. Consideriamo in Fig. 3 un ottagono, in modo che sia più chiaro il procedimento. Vogliamo, perciò, determinare C₆.

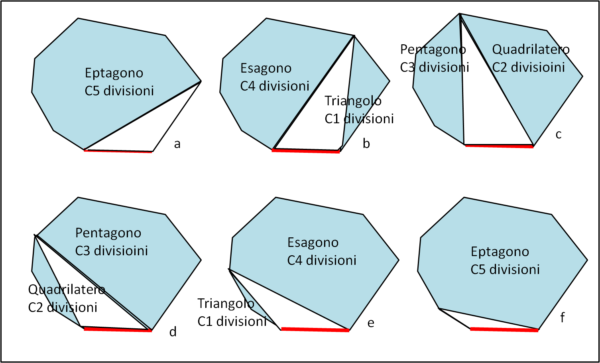
Scegliamo un lato come "base" ed evidenziamolo in rosso. Iniziamo coll'unire gli estremi della base con il primo vertice che sta alla sua destra (a). Il nostro ottagono è stato diviso in due parti del tutto indipendenti: una è un triangolo e l'altra è un eptagono. Il triangolo è quello che è e non gioca nel numero di possibili divisioni. L'eptagono possiede invece C5 possibili divisioni. Per cui questa prima conformazione porta a C5 divisioni. Consideriamo il vertice seguente e uniamolo con la base (b). In tal modo, a parte il solito triangolo che contiene la base, abbiamo ottenuto un triangolo e un esagono. Il che comporta un totale di C₁C₄ divisioni. C1 è uguale a 1 e quindi il numero di divisioni è indipendente dal triangolo che comporta un solo modo di agire.  Spostiamo ancora il vertice (c) e ci troviamo davanti un quadrilatero e un pentagono, per cui dobbiamo calcolare C₂C₃. In altre parole, l'esagono può seguire C₃ combinazioni che devono essere ammesse per i due casi contemplati dal quadrato (C₂ = 2). Cambiamo il vertice e otteniamo si nuovo un pentagono e un quadrilatero, ossia C₃C₃. Proseguendo si ottiene C₄C₁ e, infine C₅. Per simmetria moltiplichiamo il primo e l'ultimo termine per C₀ (vale 1 e non cambia niente). In conclusione:

C₆ = C₀C₅ + C₁C₄ + C₂C₃ + C₃C₂ + C₄C₁ + C₅C₀ = 1 · 42 + 1 · 14 + 2 · 5 + 5 · 2 + 14 · 1 + 42 · 1

C₆ = 132

A prima vista sembrerebbe una serie di limitata importanza (non per niente è stata trascurata per quasi un secolo), ma grazie a Catalan acquistò un nuovo e inaspettato valore e oggi è applicata a centinaia di casi pratici. La prossima volta ne citeremo qualcuno e daremo anche la formula tale da permettere di calcolare qualsiasi C_n.