Il concetto di infinito è sempre stato uno scoglio non indifferente nella storia della matematica. Ancora oggi è facile trovarsi di fronte a visioni personali e  controverse.

Un punto fondamentale è, comunque, non pretendere che il simbolo di infinito rappresenti veramente un numero. Viene spesso usato come tale, rischiando di creare paradossi o malintesi. Scriviamo spesso operazioni del tipo 1/0 = ∞ o 1/∞ = 0. Una simbologia che non deve però far trascurare il concetto di passaggio al limite.

In questo articolo, vogliamo proporre un problema matematico che ha dato il via a molte considerazioni concettualmente non banali, che può, però, essere sintetizzato abbastanza facilmente...  Ciò che  interessa, in modo particolare, è vedere come anche la matematica odierna si allacci spesso a quella di migliaia di anni fa.

Il primo quesito è il seguente:

Dato un qualsiasi numero intero N è sempre possibile trovare N punti del piano, non appartenenti a una stessa retta, che abbiano distanze reciproche pari a numeri interi? **

La risposta risulta abbastanza semplice: SI

Questa affermazione è stata seguita da un altro quesito decisamente più complicato:

Il numero di punti nel piano, aventi distanze reciproche intere e non appartenenti a una stessa retta, è infinito? ****

In questo caso la risposta è NO.

Sembra quasi che il secondo sia in contrasto con il primo, ma non è così, pensando nuovamente che infinito non è assolutamente un numero come tutti gli altri. Basterebbe ricordare che posso sempre fare la differenza tra numeri interi grandi a piacere, ma non ha praticamente senso fare ∞ - ∞. Così come ha ben poco senso parlare di multipli o divisori di infinito e via dicendo.

 

Affrontiamo il primo  problema.

Innanzitutto, è banale notare come  sarebbe molto facile inserire N punti su una retta in modo che la distanza tra due punti sia sempre uguale a un intero. Basterebbe inserire i punti su un asse rettilineo e distanziarli di un'unità. Immediatamente, avremmo risolto il problema dato che qualsiasi distanza reciproca sarebbe sempre pari a un numeri intero, essendo una differenza tra numeri interi e, perciò, sicuramente un intero.

Escludiamo, perciò, questo caso e imponiamo che NON tutti siano su una stessa retta. Ovviamente per N = 3, la soluzione è immediata: basta considerare l'asse tra due punti A e B che abbiano distanza intera: qualsiasi punto P dell'asse a distanza intera da A avrebbe (triangolo isoscele) pari distanza intera anche da B.

Le cose si complicano per N sempre più grande... Risolviamo la faccenda richiamando qualcosa già conosciuta dai babilonesi, come dimostra una tavoletta di argilla incisa 1800 anni prima di Cristo...

Per rendere il tutto ancora più semplice, iniziamo limitandoci a distanze tra punti che siano numeri razionali, ossia frazioni di numeri interi  diversi da zero. Costruiamo il triangolo rettangolo di Fig. 1a.

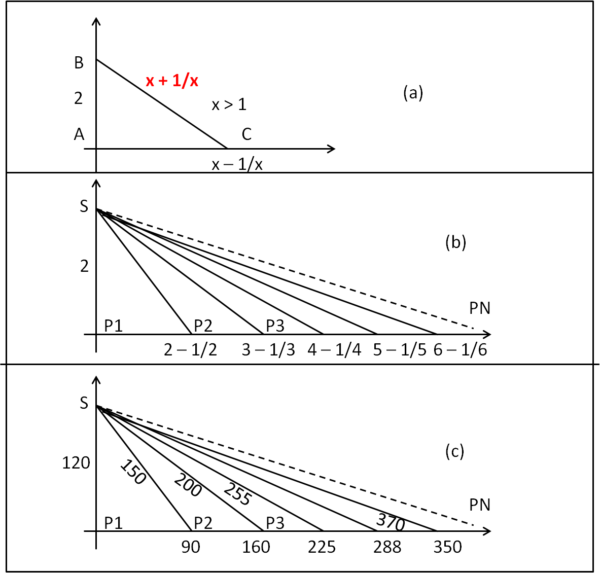
La distanza tra AB sia un numero intero, ad esempio 2. Poniamo il terzo punto C lungo l'asse x  tale da distare (x - 1/x) da A, con x intero maggiore di 1. AC corrisponde a un numero sicuramente razionale Quanto vale BC?

Noi conosciamo il teorema di Pitagora e possiamo scrivere tranquillamente:

BC² = AC² + AB²

BC² = (x - 1/x)² + 2² = x² + 1/x² - 2 + 4 =  x² + 1/x² + 2 = (x + 1/x)²

BC = x + 1/x

Ne segue che anche BC deve essere razionale. E', perciò, facile costruire triangoli rettangoli di cateti uguali a 2 e a x - 1/x, sicuri che anche l'ipotenusa sia un numero razionale. Detto in altre parole, è possibile costruire un triangolo con ipotenusa razionale che abbia anche i suoi cateti razionali. Da qui alle terne pitagoriche il passo è brevissimo. Basta infatti moltiplicare tutti e tre i lati per x e ottenere numeri interi!

Il fatto è che una serie di terne pitagoriche, costruite in questo modo, appare proprio nella tavoletta babilonese.

Il che implica che essi conoscevano sicuramente le terne pitagoriche e probabilmente lo stesso teorema che tutti chiamiamo, oggi, di Pitagora!

Torniamo al  nostro problema che è ormai di facile dimostrazione:

Costruiamo, in Fig. 1b, una serie di  triangoli con lo stesso cateto minore (ad esempio 2) e poi prendiamo N punti sull'asse orizzontale che abbiano ascissa (x - 1/x). Per quanto appena dimostrato, siamo sicuri che anche l'ipotenusa deve essere sempre razionale e uguale a (x + 1/x). Poniamo N = 6. Bene, le ascisse dei punti siano 2 - 1/2, 3 - 1/3, 4 - 1/4, 5 -1/5, 6 - 1/6. Le ipotenuse sono, di conseguenza, 2 + 1/2, 3 + 1/3, 4 + 4, 5 + 1/5, 6 + 1/6. Come trasformare tutte le lunghezze in numeri interi. Ovvio... basta moltiplicarle tutte per il minimo comune multiplo di 2, 3, 4, 5 e 6 che è 60, come mostra la Fig. 1c.

Lo stesso approccio può essere ovviamente usato per qualsiasi N intero, dato che basta trovare il minimo comune multiplo dei vari valori di x.

Abbiamo dimostrato che esistono sempre gli N numeri.

Ma N può anche essere infinito? E qui le cose si complicano un po'... soprattutto concettualmente.

Se considerassimo tutti i punti a distanza 1 su una retta, potremmo concludere che il numero N tende sicuramente a infinito, dato che i numeri interi sono infiniti.  Ma noi vogliamo che non stiano tutti su una retta e qui la faccenda si ingarbuglia... Per trasformare, infatti, gli N numeri razionali in numeri interi devo moltiplicarli per il loro minimo comune multiplo. Il minimo comune multiplo di un certo insieme di numeri interi deve essere divisibile per tutti gli interi dell'insieme. Tuttavia, dato che i numeri interi sono infiniti non esiste un numero intero che sia multiplo di tutti i numeri.

Qualcuno potrebbe dire che il numero esiste ed è proprio infinito, ma sappiamo che infinito non può essere considerato un vero numero. Un discorso molto delicato, che ha dato luogo a molti dubbi interpretativi. Ne segue che il ragionamento appena fatto non è stato considerato come risultato valido per la seconda domanda.  E' stato necessario utilizzare un approccio diverso che ha soddisfatto tutti, ma che, nella sua versione più intuitiva, ha avuto bisogno di un teorema che risale al grande Apollonio, che ben conosciamo per il suo amore sfrenato per le coniche.

Ribadiamo il problema: se i punti si potessero scegliere su una retta essi potrebbero essere infiniti. Ma cosa molto diversa sarebbe dire che: "Esiste un multiplo di tutti i numeri e questo vale infinito".

Il problema è stato risolto, in modo estremamente elegante, da Paul Erdos, grande matematico ungherese, morto nel  1996 . Solo nel 2024 è stato presentato un metodo più sofisticato, ma la sua sola lettura è estremamente complicata. Limitiamoci, perciò, ad Erdos e ad ... Apollonio.

Scriviamo esattamente ciò che è stato dimostrato nel 1945:

Sia S un insieme di punti di un piano, non tutti allineati. Se la distanza tra ciascuna coppia di tali punti è un intero, allora tale insieme deve essere finito.

Prendiamo due punti A e B che distino 3 unità. Esiste sempre una retta AB. Il terzo punto  C non deve essere su tale retta. Ad esempio, può trovarsi a distanza 3 sia da A che da B lungo l'asse del segmento AB. Basta, infatti, prendere C su tale asse tale che AB sia uguale a 3. La stessa distanza è anche quella tra C e B. E' facile costruire questo triangolo equilatero.

In generale, il punto C, può essere scelto ovunque, a parte appartenere all'asse o alla retta stessa AB? Assolutamente no. Se, però, esso si trovasse a una distanza pari a  un numero intero sia da A che da B, farebbe al caso nostro. In altre parole parole, sia CA che CB dovrebbero essere interi. Il triangolo ABC avrebbe i tre lati interi. Tuttavia, sappiamo che in ogni triangolo vele sempre la relazione:

CA ≤ AB + BC

ossia

CA  ≤ 3 + BC

o, ancora:

|CA - BC| ≤ 3

Il che vuol dire che tale differenza, deve essere sicuramente un intero tra 0 e 3 (la differenza tra due interi è sempre un intero). Esistono, perciò 4 possibili casi. Nel caso fosse 0, cadremmo nel caso di punti P simili a C, ossia che stanno sull'asse di AB.  Poniamo la differenza uguale a 1. Cosa vuol dire? Semplice: |PA - CB| = 1. Ma questo significa che tali punti P devono stare su un ramo di iperbole che ha A e B come fuochi. Ricordiamo, infatti, la definizione geometrica dell'iperbole: luogo dei punti che abbiano costante la differenza delle distanze da due punti (A e B) detti fuochi. Ovviamente, vale anche l'altro ramo della stessa iperbole.

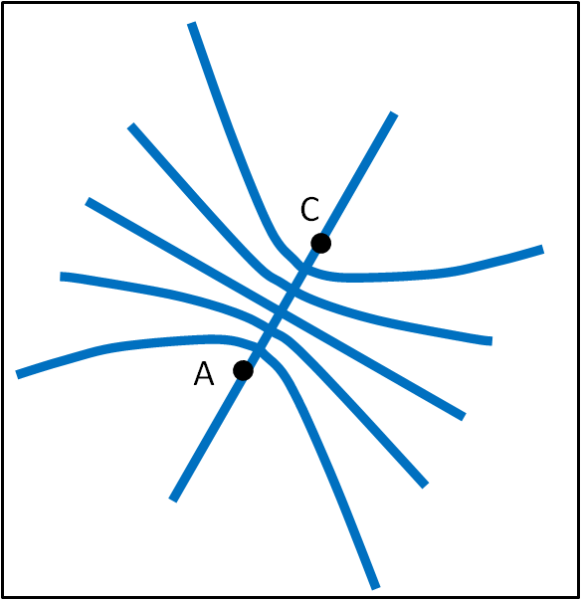
Passiamo al valore 2. Vale lo stesso ragionamento, cambiando solo i rami dell'iperbole. Infine, eccoci al caso uguale a 3, ossia |PA - PB| = 3. Ciò è possibile solo per punti che appartengano alla retta AB. Nell'ipotesi di considerare solo 3 punti del piano, possiamo rappresentare le possibili posizioni attraverso la Fig. 2. Due iperboli degeneri (retta orizzontale e verticale) e due iperboli non degeneri. Ovviamente, non tutti i punti di queste curve fanno al caso nostro, ma solo quelli che abbiano distanze intere da A e B.

Anche se non sembra, siamo già a un buon punto... Abbiamo trovato che NON tutti i punti del piano possono soddisfare le nostre richieste, ma solo quelli che stanno su una delle 4 iperboli.

Resta, però, un fatto indiscusso: ciascuna iperbole contiene un numero infinito di punti. Ne segue che l'insieme S potrebbe essere infinito. Prendiamo allora un punto R tale che abbia distanza intera sia da A che da C, che avevamo posto anch'esso uguale a 3. Il discorso fatto finora può essere ripetuto per i punti A e C. In altre parole, possiamo facilmente costruire le iperboli che definiscono il luogo dei punti R che soddisfano le nostre ipotesi.

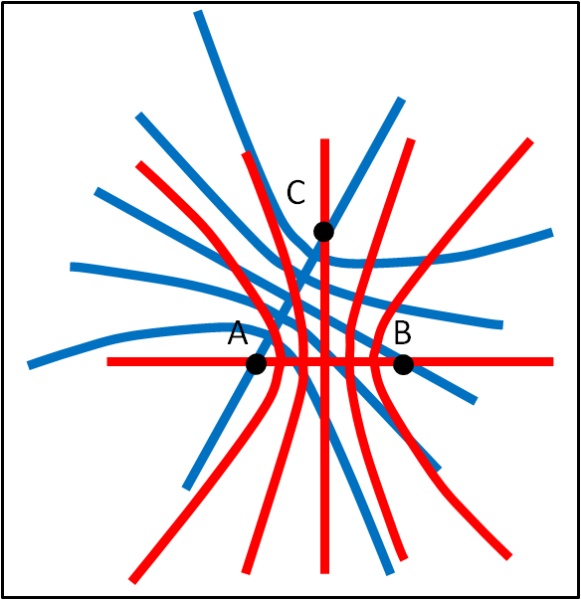
Otteniamo, perciò, la Fig. 3, dove abbiamo le possibili posizioni del quarto punto R (altre 4 iperboli).

Le intersezioni tra i due gruppi di iperboli soddisfano le nostre aspettative (Fig. 4).

In particolare, consideriamo un iperbole del primo gruppo di 3 punti e una del secondo gruppo. Quali possono essere i punti S che soddisfino distanze reciproche intere? Ovvio: le intersezioni tra queste due iperboli! Dalla Fig. 5 saltano subito all'occhio 4 intersezioni.

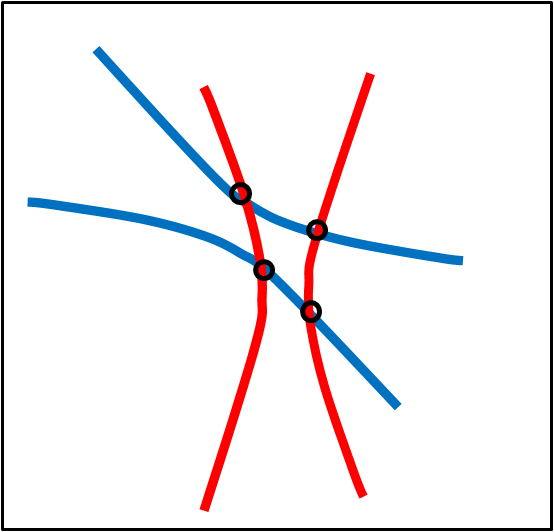
Ve ne possono essere altre fuori dal foglio? NO e questo risultato era stato già provato da Apollonio nel 200 a.C. In parole ancora più semplici, due iperboli (in generale, due coniche distinte) possono avere AL MASSIMO 4 intersezioni.

Nel nostro esempio, abbiamo, in totale, quattro iperboli del primo tipo e 4 del secondo. Ne segue che il numero di punti che soddisfano le nostre richieste DEVE essere minore o uguale a 4 · 4 · 4 (quattro iperboli di un tipo, quattro del secondo e quattro intersezioni per ciascuna coppia). Esistono, perciò, SOLTANTO 64 punti S.

Abbiamo dimostrato che nel nostro semplice esempio l'insieme S dei punti è FINITO. Ma il discorso si può facilmente estendere a qualsiasi altro triangolo di partenza i cui lati formino, ad esempio,  una terna pitagorica. Prendiamone una riportata proprio dai babilonesi nella loro tavoletta: 65, 72, 97. Facilissimo calcolare il MASSIMO  numero di punti S:

66 · 73 · 4 = 19 272

66 e 73 sono la misura dei cateti a cui è stata aggiunta un'unità, come fatto nel caso di partenza (3, 3, 3). Ovviamente, 4 rimane sempre 4, come dimostrato da Apollonio.

Esistono infinite terne pitagoriche, ma il numero di intersezioni che otteniamo è dato  dal prodotto di numeri interi e come tale deve essere un NUMERO FINITO. Nessun numero moltiplicato un altro può, infatti, dare come risultato infinito.

N1 · N2 · 4 ≠ ∞      sempre!

Così come:

∞/N --> ∞ ≠ M    M numero finito!

E' sì, è proprio vero... è facile perdersi tra finiti e infiniti e lo sapeva bene anche Leopardi...