Negli articoli precedenti (QUI, QUI e QUI), abbiamo imparato a lavorare con le tensioni e abbiamo introdotto le macchine semplici con i loro vantaggi pratici. Avendo considerato casi molto banali non vi è stata mai una vera necessità di valutare i movimenti relativi delle masse in gioco. Mi spiego meglio: nel caso della macchina di Atwood, ad esempio, è stato immediato constatare "a priori" che tanto si muoveva uno dei due pesi e tanto doveva fare anche il secondo. La fune collegava direttamente la prima con la seconda massa, per cui il sistema doveva muoversi in modo solidale. Avendo aggiunto una carrucola fissa è stato ovvio constatare che tanto una massa si muoveva vero il basso e tanto l'altra doveva muoversi verso l'alto. In poche parole, le due velocità dovevano essere uguali, anche se di segno opposto. Il che comportava che non vi fosse un reale vantaggio meccanico.

Non vi è stato bisogno di introdurre, realmente, un punto fondamentale, la costanza della lunghezza della fune. Quando abbiamo aggiunto la carrucola mobile, abbiamo facilmente concluso che la velocità del peso applicato alla carrucola mobile dovesse muoversi di una quantità pari alla metà di quella applicata al capo libero della fune. Ciò che avevamo guadagnato in forza lo avevamo perso nello spazio percorso. Il vantaggio meccanico era di 2 a 1.

In pratica, per valutare i movimenti delle varie parti abbiamo utilizzato la costanza della lunghezza della fune. Questa operazione è passata quasi inosservata, ma può diventare sempre meno banale quando il sistema diventa più complicato. In poche parole, la relazione tra le velocità in gioco è di fondamentale importanza. E per valutarla correttamente è necessario analizzare attentamente la lunghezza della fune, i suoi punti fissi e quelli mobili.

Per comprendere meglio la procedura da seguire, ripetiamo l'analisi del sistema composto della carrucola fissa e da quella mobile, trattata la volta scorsa (Fig. 1). Il problema può essere posto come segue: Imprimiamo una certa velocità vA costante al capo della fune A. Ci chiediamo quanto vale la velocità del peso M?

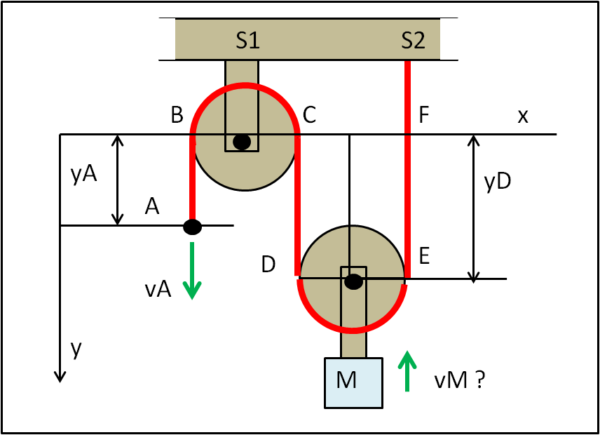
Tracciamo un asse di riferimento da cui misurare i vari tratti di fune.  Potremmo prendere S1S2, che rappresenta il soffitto, fisso, ma è ancora più conveniente considerare BC, dato che la carrucola fissa è ancorata al soffitto.  Il primo tratto di fune  è AB, ossia yA.  Poi la fune segue il semicerchio BC. La sua lunghezza rimane costante e la chiamiamo c1.  La fune scende fino a D. CD è uguale a yD . Nuovo semicerchio DE (c2) e poi salita fino a F, ossia tratto yE = yD. In realtà, manca ancora il pezzo FS2, ma quest'ultimo è un tratto che non può variare dato che E non può andare più in alto di F

Possiamo scrivere la lunghezza della fune attraverso la somma dei suoi tratti così evidenziati:

L = yA  + c1 + yD + c2 + yD + FS2.

Notiamo che la lunghezza di alcuni tratti varia nel tempo, mentre per altri rimane costante. Come detto, noi siamo interessati alle variazioni dei punti mobili rispetto al tempo, dato che vogliamo ottenere la loro velocità. Non ci resta, quindi, che derivare la lunghezza L, ossia calcolare la sua variazione rispetto al tempo. L, però, deve rimanere costante, per cui la sua derivata è uguale a zero. Così come sono uguali a zero le derivate dei tratti che rimangono costanti nel tempo. Ne risulta perciò:

0 = dyA/dt + 2 dyD/dt

Per cui:

vA + 2vD = 0

vD  è anche la velocità con cui si muove la massa M, solidale con la carrucola mobile. per cui:

vM = - 1/2 vA

Questa relazione ci dice che a seguito del movimento di A con velocità vA, il peso M si muove con una velocità che è la metà di quella di A, e che va in verso opposto, come indica il segno meno. Se A scende, M deve salire. Il rapporto tra le velocità ci dice, ovviamente, anche qual è il vantaggio meccanico del sistema.

Non ridete... abbiamo ottenuto con inutile fatica ciò che era facilmente prevedibile. Tuttavia, come già detto, questo banale calcolo diventa essenziale per sistemi più complessi e meno prevedibili.

Prendiamo, ad esempio, il caso di Fig. 2

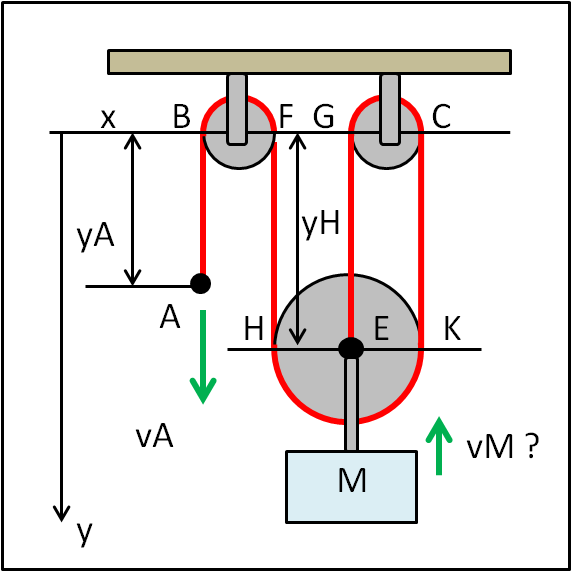
Imprimiamo una velocità vA al capo libero della fune A. Vogliamo calcolare la velocità del peso M.

I punti B,F,G e C possono essere considerati fissi al soffitto. Per cui possiamo prendere la retta che li congiunge come asse di riferimento.

Iniziamo a scrivere la lunghezza della fune partendo da A. Il primo tratto è yA = AB. Questo è un tratto di lunghezza  che varia in funzione del movimento di A. Abbiamo poi  la semicirconferenza BF che rimane costante e la chiamiamo c1. Segue FH che è uguale a yH e che è variabile. Vi è, dopo, la semicirconferenza HK di lunghezza, ovviamente, costante che chiamiamo c2. Proseguendo, abbiamo il tratto variabile CK = yH. Nuova semicirconferenza CG = c3. Infine il tratto GE che è ancora uguale a yH.

Ne segue che la lunghezza L della fune può essere scritta come:

yA + c1 +yH + c2 + yH + c3 + yH = L

Facciamo la derivata rispetto al tempo, sapendo che c1, c2 e c3 sono costanti, così come tutta la lunghezza L

dyA/dt + 3dyH/dt = 0

vA + 3 vH = 0

vH = - 1/3 vA

Ma vH è  uguale a vE e, quindi, anche a vM che è solidale con la carrucola in basso di centro E.

Per cui il nostro peso M si alza (abbiamo un segno opposto allo spostamento di A) con una velocità pari a 1/3 di quella di A. Il che significa anche che il sistema ha un vantaggio meccanico di 3 a 1. Tanto si guadagna in forza motrice, tanto si deve perdere in lunghezza.

Consideriamo, in Fig. 3, un altro caso, ancora piuttosto semplice, in cui aggiungiamo una carrucola mobile e utilizziamo due funi.

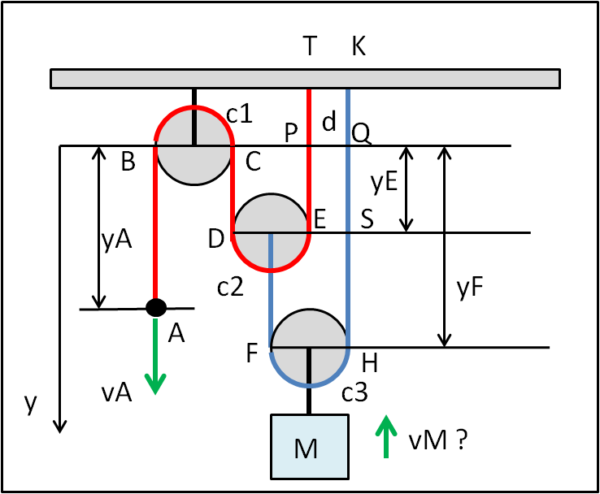
Come prima, imprimiamo una velocità vA al punto A della prima fune, tirando verso il basso. Cose mi muoverà il peso M? E, di conseguenza, quale sarà il vantaggio meccanico?

Prendiamo la retta BCQ come linea di riferimento per gli spostamenti della fune. Notiamo che TP e KQ sono tratti di fune che rimangono costanti, dato che E e H non possono certo salire più in alto di P e Q.

Sveltendo i calcoli, "sezioniamo" la fune L1, partendo da A:

abbiamo yA = AB, poi la semicirconferenza c1, quindi yD = yE = CD. Segue la semicirconferenza c2 e infine PE = yE = yD. Come già detto, il tratto EP è una costante che possiamo chiamare p. Ne segue :

L1 = yA + c1 + yD + c2 + yD + p = yA + 2yD + c1 + c2 + d

Possiamo scrivere la lunghezza della seconda fune, come segue:

L2 = d + QH +c3 + FE  =  d + yH + c3 + (yH - yD)

L2 = 2yH - yD + d + c3

Deriviamo sia L1 che L2, ottenendo:

0 = vA + 2vD

0 = 2vH - vD

dalla seconda

vD = 2vH

sostituendo nella prima

yA + 4vH = 0

ossia

vH = -1/4 vA

Ovviamente, la velocità vH è proprio quella del peso M, per cui il peso M si alza con una velocità che è 1/4 di quella di A verso l'alto, come indica il segno meno. Il vantaggio è salito a 4 a 1.

Vi lascio due esercizi che potete benissimo risolvere da soli. Se volete inserirli nei commenti sarebbe una bella cosa. Tra qualche giorno, comunque, li risolveremo insieme...

QUIZ (1) **

Il sistema è quello di Fig.4.

Imprimendo una velocità vB alla carrucola mobile B, determinare la velocità di A.

QUIZ (2) ***

Il sistema è quello di Fig. 5.

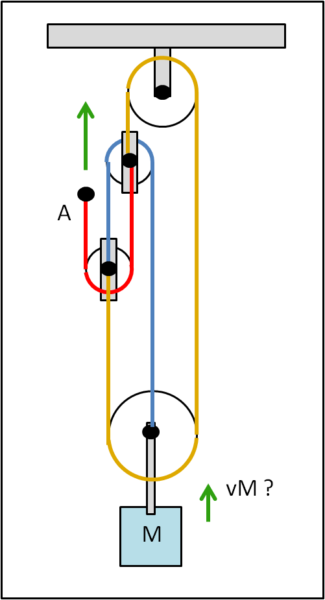
Vi sono tre carrucole mobili e una fissa. Imprimendo una velocità vA ad A, come si muove M?