Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Cercare di analizzare la cardinalità di R senza prima parlare della continuità  che lo caratterizza  è assurdo; le dimostrazioni infatti si appoggiano appunto sulla continuità dei numeri reali. E' per questo che l'ordine di infinito di R è diverso (come vedremo) da quello degli insiemi numerabili: a causa della continuità.  Lo stesso Cantor per primo, fece una costruzione dei numeri reali  per raggiungere lo scopo, noi considereremo però la costruzione di Dedekind.

Nell'articolo precedente, abbiamo disposto i numeri razionali sulla retta, usando una certa unità di misura, e visto che i razionali sono un insieme denso.

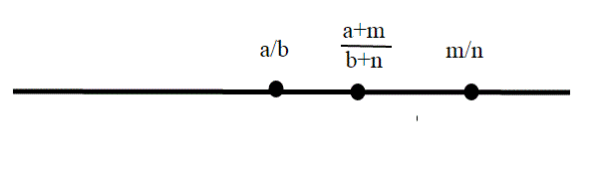
Pur essendo Q denso ( ovvero fra qualsiasi coppia di razionali ne troviamo sempre un altro) Q non copre tutta la retta . Infatti  non è un numero razionale.Lo abbiamo visto nel primo articolo sugli insiemi, riporto qui il link:Radice di due non è razionale

Da qui la necessità di introdurre un nuovo insieme numerico, quello dei numeri reali, che contiene anche i numeri detti "irrazionali".

Approssimare

Tutti pensiamo di saper calcolare ; basta prendere una calcolatrice per ottenere un risultato di questo tipo, a seconda della calcolatrice:

1,4142

(prima della calcolatrice esistevano vari algoritmi per il calcolo, già dai tempi dei Persiani e dei Babilonesi) in realtà questo numero non è radice di due, ma solo una sua approssimazione usando i decimali. Però senza ombra di dubbio, considerando solo le prime due cifre dopo la virgola, sappiamo che   è un numero compreso fra 1,41 e 1,42 che scritto in frazioni decimali porta alla seguente disuguaglianza:

1+4/10+1/100<  < 1+4/10+2/100 ovvero:

141/100< < 142/100

che si può verificare semplicemente elevando al quadrato il primo ,il secondo e il terzo membro (se x è positivo,  è equivalente a dire x<,   è equivalente a dire x>) . Notare che la lunghezza di questo intervallo è 1/100; se consideriamo 1,414 , 1+4/10+1/100 + 4/1000<  < 1,414 , 1+4/10+1/100 + 5/1000 ovvero 1414/1000< < 1415/1000 otteniamo una stima maggiore,e  risulta confinata in un intervallo di larghezza 1/1000. aumentando sempre di più la precisione da una parte ottengo  dei numeri razionali il cui quadrato è minore di 2 (le approssimazioni per difetto), dall'altra quelli il cui quadrato è maggiore di 2 (le approssimazioni per eccesso).

La costruzione di Dedekind

Anche se è un  impresa ardua, vorrei dare una giustificazione della continuità dei reali. Richard Dedekind (1831–1916) riuscì a definire i numeri reali come estensione dei numeri razionali. Fece cioè una costruzione, definendo un numero reale partendo dai razionali: lo scopo principale era quello di risolvere tutte le equazioni del tipo   che non sempre hanno soluzione razionale. Egli diede innanzitutto una definizione: chiamiamo sezione di Q ogni coppia di insiemi A , B che soddisfino le seguenti proprietà:

1)A e B siano non vuoti,

2) A e B non abbiano elementi in comune e la loro  unione dia  A U B=Q.

3) Qualsiasi elemento di A è minore di qualsiasi elemento di B.

Vediamo due esempi di sezione. L'eventuale elemento x di Q che sta in mezzo ai due insiemi (A,B)  a<=x <= b) si dice elemento separatore. Facciamo due esempi:

A={a<=1/2}, B={b>1/2} questa è una sezione di Q; l'elemento separatore è 1/2. La sezione si dice di prima specie.

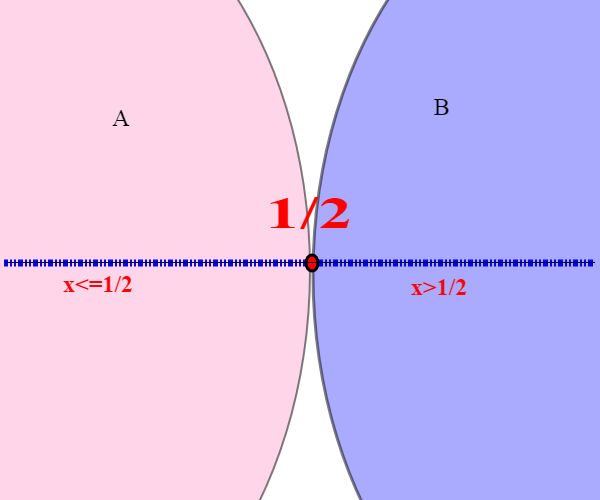
Consideriamo ora la seguente sezione di Q:

A={q <=0, q appartenente a Q} U {q>0, , q appartenente a Q}

B={, q appartenente a Q}; questi insiemi sono disgiunti, la loro unione dà Q e ogni elemento d A è minore di ogni elemento di B. Altro non sono che le approssimazioni per difetto e per eccesso di .

 

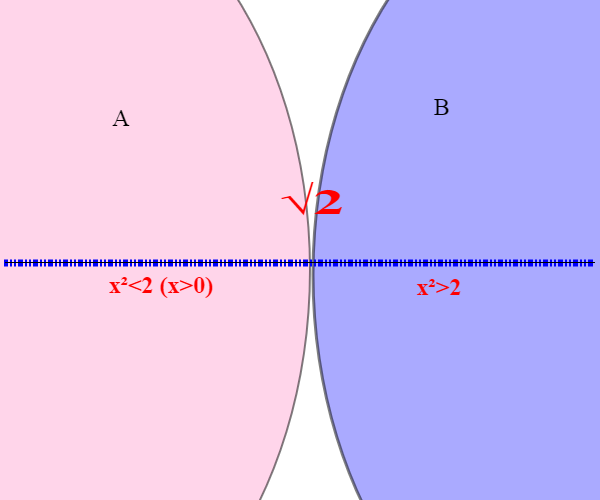
Però non esiste alcun elemento in mezzo alle due sezioni ( non è razionale!); la sezione si dice di seconda specie. Per dirla con le  parole di Dedekind:

...Ora, in ogni caso in cui c’è una sezione (A, B) che non è prodotta da un numero razionale, allora noi creiamo un nuovo numero irrazionale a che riteniamo completamente definito da questa sezione; diremo che questo numero a corrisponde a questa sezione oppure che produce questa sezione.

In questo modo definisce i numeri reali come sezioni di numeri razionali, riempendo i buchi con le sezioni di seconda specie.

Ma un numero reale è un numero, come può essere definito come un coppia (A,B) di insiemi con certe caratteristiche? Basta definire opportunamente le operazioni e verificare poi le proprietà formali (non spaventatevi sul termine proprietà formali; non sono che altro che le proprietà che abbiamo sempre applicato nelle espressioni algebriche studiate alle superiori) . La verifica di tutte le proprietà formali è una cosa lunga e noiosa. Noi le prenderemo per buone. La cosa più importante per noi è l'assioma di completezza, che in realtà non è un assioma, ma un teorema dimostrato partendo dalla definizione di numero reale come sezione. Dedekind estende per similitudine le sezioni anche nel campo dei numeri reali, e dimostra che nei reali ogni sezione di numeri  è di prima specie, ovvero (a differenza dei razionali) esiste sempre un numero reale che le separa.

In pratica  la'assioma di completezza è una conseguenza del fatto  che ogni sezione di numeri reali è di prima specie.

Prima di enunciare l'assioma di completezza di R, abbiamo bisogno di alcune definizioni che riguardano  R, in quanto insieme totalmente ordinato. Cosa vuol dire? Un insieme in cui sia presente un ordinamento, ovvero in parole povere dotato di un confronto fra qualsiasi coppia di elementi che gli appartengono. Sappiamo cioè decidere dati a, b diversi, se a<b, o a >b, qualsiasi siano a e b. Questo ordinamento ci permette poi di definire:

 Gli Intervalli in R.

Intervalli limitati.

Premetto che la scrittura a<=b significa semplicemente che a è minore o uguale a b. Analogamente per a>=b.

Siano a e b due numeri reali tali che a < b. L’ intervallo aperto di estremi a e b è l’insieme (a, b) = {x appartenente ad R tale che a < x < b}; a è il primo estremo, b il secondo estremo. L’intervallo chiuso di estremi a e b è l’insieme [a, b] = {x appartiene ad R tale che a<= x<= b}. In
maniera analoga si definiscono l’intervallo semiaperto a destra [a, b) e l’intervallo semiaperto
a sinistra (a, b] mediante le disuguaglianze a< x =< b e a < x<= b. In ciascuno dei casi si definisce lunghezza dell'intervallo la differenza fra gli estremi l=b-a.

intervalli illimitati

[a,)={x appartiene ad R : a<= x}

(a,)={x appartiene ad R : a< x}

(,a)={x appartiene ad R : x<a}

(,a]={x appartiene ad R : x<=a}

la notazione include  i simboli ,; è puramente simbolica, praticamente ci dice che possiamo andare a destra e sinistra sulla retta reale quanto vogliamo; ,  non sono numeri reali, non potremmo in ogni caso definire somme e prodotti che li contengono.

Minoranti  di un un sottoinsieme di R

Sia S un sottoinsieme non vuoto di R. Diremo che un elemento a di R é un minorante di S se a<= s per ogni s appartenente a S.

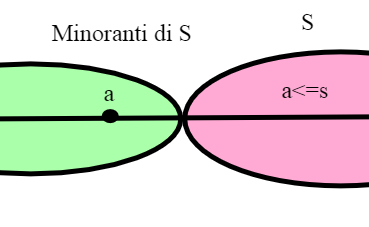
Un insieme S si dice inferiormente limitato se esiste almeno un minorante di S. Un minorante di S che appartiene a S si dice minimo di S.  Un insieme può avere al più un minimo, e lo indichiamo con min S.

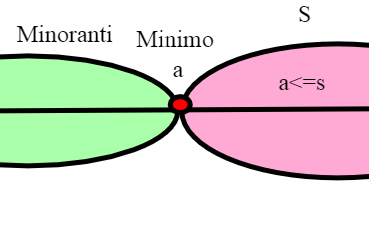
Unicità del minimo
Infatti, se a e  sono minoranti di S e appartengono entrambi a S, si ha a <=  e <= a quindi a= .

Maggioranti  di un un sottoinsieme di R

Analogamente diremo che elemento b di R è un maggiorante di S se s<= b per ogni x appartenente a S.

S è inferiormente illimitato se l’insieme dei minoranti di S è vuoto.

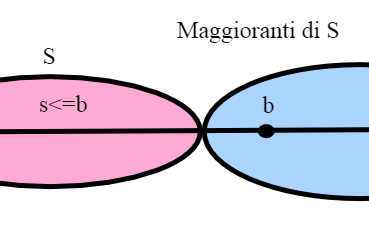
Un insieme si dice superiormente limitato se se esiste almeno un maggiorante di S, superiormente illimitato se l'insieme dei maggioranti è vuoto.

Un maggiorante di S che appartiene a S si dice massimo di S, e lo indichiamo con max S.

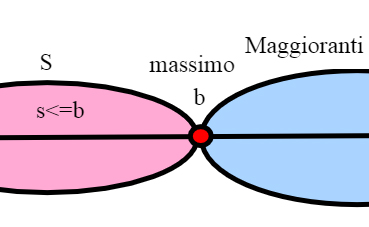
Unicità del massimo

Infatti, se a e  sono maggioranti di S e appartengono entrambi a S, si ha a >=  e >= a quindi a=

Un insieme si dice limitato se è superiormente e inferiormente limitato.

 

Estremo superiore e estremo inferiore

Se l’insieme dei minoranti di S ha massimo a si dice che a è l’estremo inferiore di S. Analogamente, se l’insieme dei maggioranti di S ha minimo b si dice che b e l’estremo superiore di S.
L’estremo inferiore e l’estremo superiore di un insieme, se esistono, sono necessariamente unici (essendo definiti come minimo e massimo di un insieme; abbiamo visto che sono unici). Essi si denotano rispettivamente con inf S e sup S. Si noti che se S ha minimo esso coincide con l’estremo inferiore. Se S ha massimo, esso coincide con l'estremo superiore.

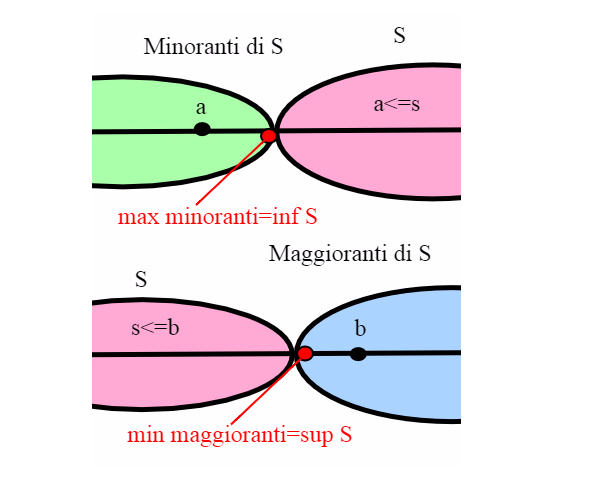
Esempi in R

Consideriamo l'intervallo S=[0,1) (chiuso a sinistra e aperto a destra).L'insieme dei minoranti è l'intervallo (,0]. infatti per definizione di insieme di minoranti, sono gli x<=0. Ma questa è proprio la definizione dell'intervallo illimitato che abbiamo dato sopra. L'estremo inferiore di S è il massimo di (,0], che è 0 che vi appartiene. Anche il minimo di S è zero, perchè zero appartiene a S. L'insieme dei maggioranti è invece l'intervallo [1,) (gli x>=1). Il minimo dei maggioranti è 1; quindi sup S=1; notiamo invece che S pur avendo estremo superiore, non ha massimo, perchè 1 non appartiene ad S. In generale, anche se un insieme è limitato , non è detto che abbia massimo o minimo. Sembra però diversa la questione per l'estremo superiore e quello inferiore. Infatti è proprio quello che ci assicura l'assioma di completezza:
Assioma di completezza o continuità.

L'assioma si può esprimere in due modi:
1)Ogni sottoinsieme non vuoto superiormente limitato di R ha estremo superiore.

2)ogni sottoinsieme non vuoto e inferiormente limitato di R ha estremo inferiore.

Le due definizioni sono equivalenti, ovvero la 1) implica la 2) e viceversa.

Facciamo vedere che 1) implica 2), ovvero che ogni sottoinsieme non vuoto e inferiormente limitato di R ha estremo inferiore

(la dimostrazione è tutta scritta nel disegno,penso che così si possa visualizzarla meglio).

Osservazione su Q e R

Qualcuno sarebbe tentato di dire ; ma Q è denso, possiamo trovare quanti razionali vogliamo in un piccolo intervallo, quindi l'assioma di completezza potrebbe  valere anche per Q, che è un insieme totalmente ordinato.  NO.  Consideriamo in Q l'insieme:

S={ q appartenenti a Q, q>o , } ; questo insieme non è vuoto (),  è superiormente limitato (lo stesso numero 2 è un maggiorante, in quanto il quadrato di 2 è 4 e quindi 2 non appartiene ad S) , ma non ha estremo superiore in Q. Intuitivamente possiamo dire questo;per l'assioma di continuità in R l'estremo superiore esiste ed è  (andrebbe dimostrato formalmente, ma senz'altro  è il primo candidato), ma sappiamo che  non appartiene a Q (non è un numero razionale). Quindi in Q  l'insieme S non ha estremo inferiore.

Conseguenze dell'assioma.

Una prima conseguenza dell'assioma, è che se b è l'estremo superiore di un insieme S , allora esistono elementi di S arbitrariamente vicini a b=sup S.

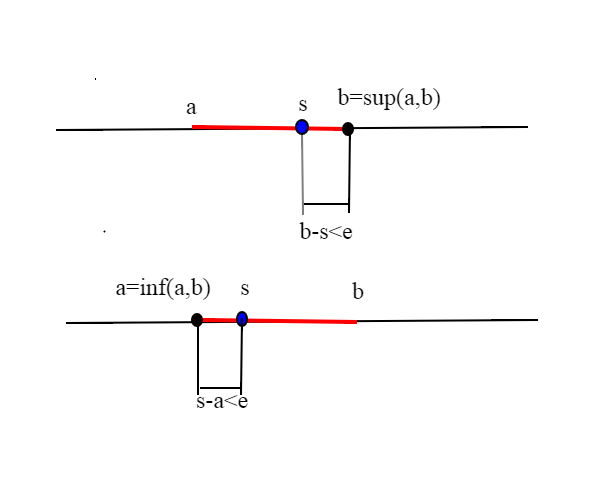
allo stesso modo se a=inf S, esistono punti di S arbitrariamente vicini ad a=inf S. Vediamolo nel primo  caso di b=sup S; comunque prendiamo un qualsiasi  numero e>0, dobbiamo dimostrare che esiste un elemento s appartenente ad S, tale che b-s<e; se esistesse un numero e per cui non è vera l'affermazione, vorrebbe dire che per ogni s appartenente ad S  b-s>=e, ovvero s<=b-e; allora b-e sarebbe un maggiorante di S minore di b=sup S, contrariamente all'ipotesi che b sia il minimo dei maggioranti.

Questa è una prima conseguenza dell'assioma di completezza; nel prossimo articolo ne vedremo delle altre che ci permetteranno di analizzare la cardinalità dell'insieme R .

Articoli precedenti:

Cantori, parte ottava;L'insieme delle parti e il teorema di Cantor

Cantor, parte settima La numerabilità di Q

Cantor, parte sesta:Il minimo ordine di infinito

Cantor pare quinta,Il principio di induzione

Cantor, parte quarta. L'abergo di Cantor

CANTOR parte Terza, gli insiemi numerabili

CANTOR parte Seconda: Corrispondenze e funzioni

CANTOR parte prima, gli insiemi

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica