Per una trattazione completa della Meccanica Quantistica, si consiglia di leggere il relativo approfondimento, in cui è stato inserito anche il presente articolo

 

Non spaventatevi o non illudetevi: non voglio parlare di musica lirica e nemmeno del Rigoletto. Voglio solo tornare sulla meccanica quantistica. Un’ovvia conseguenza dell’esperimento della doppia fenditura, ossia dell’accertata strana natura delle particelle che possono assumere il comportamento di onde ma anche quello di corpuscoli ben definiti, è senza dubbio il principio di indeterminazione di Heisenberg. Lo voglio affrontare a parole, come si fa quasi sempre, ma anche -e soprattutto- con un’esperienza diretta che è una semplice appendice di quella di Feynman già ampiamente trattata e sviscerata. Vedremo anche che i concetti imparati sul limite, sullo zero e infinito, sul paradosso di Zenone, sugli intervalli “finiti” tipici della fisica, ecc., avranno un’applicazione molto “pratica”.

L’esperimento della doppia fenditura ci ha posto davanti all’illogicità del comportamento delle  particelle microscopiche. Abbiamo così descritto (ma non capito) come le particelle siano capaci di scambiarsi informazioni senza aver bisogno di inviarsele effettivamente. Insomma, abbiamo dovuto  accettare il fenomeno dell’entanglement. Abbiamo anche dovuto digerire il fatto che esse si comportano sia come particelle in senso fisico sia come onde e che l’osservazione o anche solo la deduzione indiretta della loro posizione faccia collassare l’onda di probabilità che le descrive. Questa assurda realtà, che porta a fenomeni costantemente utilizzati nella vita di tutti giorni (per primi dal nostro Sole e dalle sue sorelle), implica alcune ricadute fondamentali sulla meccanica quantistica. La più famosa è forse il principio d’indeterminazione di Heisenberg.

Riprendo il discorso sulla meccanica quantistica (MQ) dal punto dove l’avevo lasciata, ossia dal problema della doppia fenditura, illustrato in modo superbo dal grande Feynman.

Ovviamente, cercherò di continuare senza usare formule complesse (finché ci riuscirò), in modo da regalarvi i concetti fondamentali piuttosto che una descrizione matematica (ci vorrebbe ben altra matematica di quella che sto cercando di spiegare in questo blog). Per descrivere il principio d’indeterminazione userò sia le solite parole, che portano automaticamente a una trattazione più complessa e che lasciano un po’ di amaro in bocca (si accettano, ma si capiscono poco), sia -soprattutto- un esempio che mi sembra altamente intuitivo e che si riallaccia a quello della doppia fenditura. Anzi, può esserne considerato una “ovvia” derivazione.

Vi consiglio di andarvi a rileggere la diffrazione luminosa  (di cui si parla QUI) per inquadrare meglio il problema, anche se certe cose potreste accettarle senza troppe spiegazioni. Ne approfitterò anche per chiarire meglio cosa s’intenda per “disturbo” dovuto alla misura che spesso porta a grandi confusioni (non solo da parte degli inesperti…).

Bando alle ciance e cominciamo.

Il principio di indeterminazione di Heisenberg dice in modo molto conciso e semplificato: “E’ impossibile misurare con la stessa precisione sia la posizione che la velocità di una particella”. In altre parole: “Quanto più si tenti di stabilire con maggiore accuratezza la posizione occupata da una particella, tanto più diventa aleatoria e incerta la sua velocità”. Potremmo dire, molto semplicemente, che il principio è di banale comprensione, sapendo ormai che una particella non occupa una certa posizione nello spazio, ma ha solo una certa probabilità di essere in un dato punto. Tuttavia, la risposta farebbe storcere un po’ il naso, dato che la faccenda può apparire sensata nella sua illogicità, ma non risulta molto chiaro il perché e il percome di questa conseguenza. Intuitivamente è accettabile, ma sarebbe molto meglio esprimere il concetto con una qualche esperienza diretta.

Potremmo cavarcela utilizzando un ragionamento legato alla fisica classica.

E’ ovvio che succeda quanto stabilito da Heisenberg. Per potere accertare la reale posizione di una particella devo innanzitutto vederla molto bene, ossia illuminarla. Ma illuminare qualcosa vuol dire inviare un fascio di fotoni che sicuramente disturba il movimento della particella. In altre parole,  per misurare la posizione di una particella, con una precisione elevata, bisogna ricorrere a una luce di lunghezza d'onda molto corta, e quindi altamente energetica. Ciò si traduce nel trasferimento di una certa quantità di moto (massa per velocità) alla particella e pertanto non è possibile misurare con esattezza la sua velocità. Alternativamente, se ci si accanisce sulla misura di quest’ultima, diventa problematico descrivere esattamente la sua posizione. Un fenomeno prettamente meccanico.

Troppo spesso nei libri e in vari articoli di pseudo-scienza ci si ferma a questa spiegazione. Essa, anche se sicuramente vera in linea di principio, ha ben poco a che fare con la MQ. In realtà, anche se riuscissimo a “vedere”, senza interagire, la situazione non cambierebbe di molto. L’impossibilità di misurare entrambe le grandezze fisiche dipende essenialmente dalle caratteristiche quantistiche intrinseche delle particelle. Il fatto che esse siano rappresentabili come onde di probabilità implica proprio che è impossibile sapere dove sia realmente la particella o -alternativamente- se si riesce a localizzarla perfettamente (in altre parole la facciamo collassare) diventa del tutto aleatoria la sua velocità.

Sì, lo so, potrei anche considerarmi soddisfatto e limitarmi alle parole, come si fa di solito e magari inserire una formuletta che lega posizione e velocità (o meglio quantità di moto) alla costante di Planck (che già conoscete). Lo farò di sicuro, ma preferisco arrivarci  proseguendo lungo il tracciato aperto da Feynman  e rifarmi all’esperienza della fenditura.

Questa volta, però, ne consideriamo una sola: ci basta e avanza. Qualcuno potrebbe subito fermarmi e dire: “No, non funziona! Sappiamo benissimo che se spariamo gli elettroni o i fotoni attraverso una sola fenditura non otteniamo assolutamente la figura d’interferenza tipica delle onde. D’altra parte è ovvio, dato che se abbiamo una sola fenditura sappiamo benissimo da dove deve passare la particella e quindi essa collassa proprio nello stato di particella”. In parte, avrebbe anche ragione, ma non del tutto. Dimenticherebbe il fenomeno della diffrazione…

Essa è quel fenomeno che ci vieta categoricamente di poter vedere al telescopio una stella come un oggetto puntiforme. La luce, intesa come onda, che passa attraverso una fenditura, deve toccare anche i bordi del foro e questi danno luogo a una nuova onda che interferisce con quella originatasi nell’altro bordo. In conclusione, l’immagine che si ottiene è ancora una figura d’interferenza con un picco di luminosità centrale molto alto, seguito da zone scure e chiare di altezza decrescente. La situazione, quindi, è ancora perfetta per dimostrare sperimentalmente il principio d’indeterminazione.

Richiamiamo brevemente il fenomeno della diffrazione (come già detto, rileggete, comunque, gli articoli già scritti) che, per semplicità, possiamo legare soltanto all’esistenza dei bordi della fenditura (il principio di Huygens andrebbe ancora più in là, ma le conclusioni sarebbero le stesse).

Immaginiamo di avere un’onda luminosa proveniente dall’infinito (quella di una stella, ad esempio), ma realizzabile anche con una strumentazione da laboratorio. Essa può essere rappresentata come linee rette parallele alla parete della fenditura. Se preferite, però, potete anche pensare a fotoni “sparati” in modo perfettamente perpendicolare alla parete: o entrano nella fenditura oppure non entrano, non ci sono vie di mezzo, tipo strani rimbalzi.

I principi dell’ottica, ma anche una visione terra-terra, ci dice che l’onda (o i fotoni…) che “tocca” la parete dà luogo a una nuova onda (se volete, chiamatela anche  probabilistica) con l’origine in quel punto. Consideriamo la Fig. 1, dove vi è la solita parete con al centro la fenditura e, più lontano, lo schermo di raccolta dei fotoni. La fenditura deve essere molto piccola, dell’ordine della lunghezza d’onda della luce.

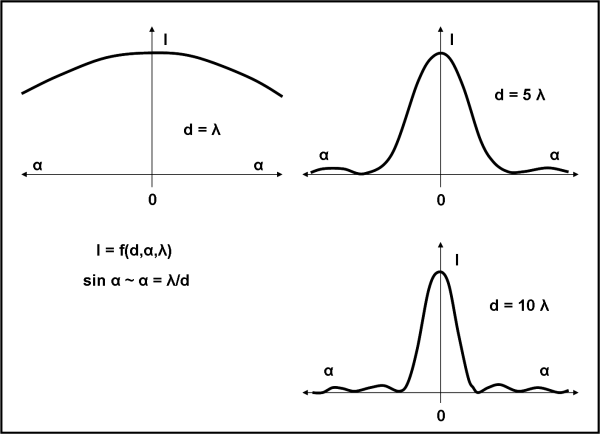
Ciò che vediamo è che l’onda piana si trasforma in un onda “quasi” sferica. L’immagine finale sullo schermo mostra un alto picco centrale e picchi laterali sempre più bassi. Proviamo a variare la larghezza della fenditura. La matematica ci dimostra facilmente che l’intensità dell’onda che tocca lo schermo finale è una funzione della larghezza della fenditura d, della lunghezza d’onda λ della luce utilizzata e della distanza dal centro dello schermo O che si misura come angolo α rispetto al centro della fenditura. In particolare, però, vale una semplicissima relazione che possiamo anche scrivere senza paura e che ci dice quanto è larga la prima banda luminosa centrale:

α = λ/d

E’ una formula che dovreste conoscere molto bene, soprattutto coloro che posseggono un telescopio e cercano (non voi sicuramente) di ottenere immagini migliori inserendo oculari e diavolerie del genere. Niente da fare: chi comanda la nitidezza dell’immagine finale (ossia le sue dimensioni) è il diametro dell’obiettivo (ossia d). Più è grande d e più piccola è la figura di diffrazione, ossia migliore è il potere risolutivo dell’obiettivo. In realtà, dovremmo far comparire il seno di α, ma gli angoli sono così piccoli che si può anche scrivere l’angolo al posto del suo seno. In ogni modo, quello che ci interessa è il poter dire che la larghezza della figura di diffrazione (che è poi l’immagine finale) aumenta al diminuire della larghezza della fenditura.

 

Vediamo la situazione in Fig. 2, in cui si sono rappresentate le immagini ottenute sullo schermo finale (ossia, le curva di luminosità) per tre valori di d.

Possiamo anche schematizzare il risultato disegnando direttamente, in Fig. 3 ,come varia l’onda luminosa dopo aver passato la fenditura. Per il nostro scopo, è utile rappresentarla con i raggi luminosi, ossia con le rette che partono dal punto d’origine dell’onda e sono ad essa perpendicolari. Non sbaglieremmo di certo nel considerare ogni raggio luminoso come una delle possibili direzioni di ogni singolo fotone, dato che essi sono proprio rappresentabili come onde di probabilità.

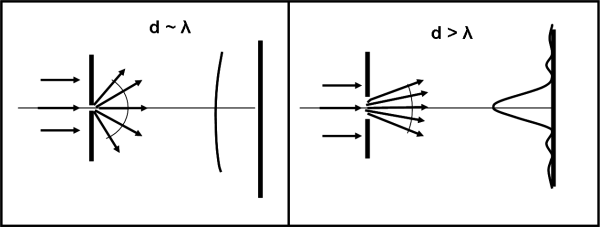
Non spaventatevi: ormai dobbiamo sapere che possiamo passare da onde alle particelle senza alcuna paura. Basta ricordare che la particella, prima di essere individuata, può benissimo essere considerata un’onda. I fotoni che escono dalla fenditura, hanno un campo di probabilità sempre più grande a mano a mano che la fenditura diminuisce, in quanto cresce l’angolo descritto dai raggi luminosi perpendicolari alla superficie dell’onda.

Questa visione, che corrisponde perfettamente ai principi dell’ottica meccanica, dimostra anche perfettamente il principio di Heisenberg. Ragioniamoci un attimo: la fenditura che decresce di dimensioni indica con sempre maggiore precisione il punto esatto dell’origine dell’onda al passaggio dalla fenditura, ossia la posizione della particella. Se, teoricamente, la fenditura diventasse puntiforme, l’onda d’uscita creerebbe un’immagine finale infinita (come vedete viviamo sempre nella continua lotta-amicizia tra zero e infinito), così come se la larghezza della fenditura tendesse a infinito, le dimensioni dell’immagine finale sarebbe puntiforme. In altre parole, se avessimo una posizione perfetta (puntiforme) della particella avremmo infinite direzioni che potrebbe seguire. Se, invece, avessimo una sola direzione perfettamente determinata, la particella potrebbe essere ovunque.

Abbiamo o non abbiamo descritto il principio d’indeterminazione di Heisenberg? Direi proprio di sì. Possiamo anche vederlo geometricamente con la Fig.4, in cui ho scelto una certa dimensione della fenditura.

Prima della fenditura, l’onda proviene dall’infinito, ossia ha i suoi raggi paralleli. Ciò vuol dire che è estremamente ben definita la direzione di provenienza e quindi anche la velocità del fotone (valore numerico, ossia c, e direzione), ma è assolutamente aleatoria la posizione del fotone che può trovarsi in un qualsiasi raggio. Ho una precisa determinazione della velocità, ma ho una scarsissima precisione nella posizione della particella che ha l’onda come rappresentazione delle sue probabilità di esistenza. So da dove proviene il fotone e con quale velocità ma non so proprio dove trovarlo: può essere ovunque.

Finalmente arriviamo alla fenditura. Tutte le posizioni del fotone che portano alla parete sono da escludere. Se fosse stato lì si troverebbe davanti una porta chiusa e si rivelerebbe collassando come particella fisica. Quelli che entrano nella fenditura possono, invece, proseguire. Tuttavia, più l’apertura della fenditura è piccola e più si determina con esattezza la posizione del fotone “fortunato”. Qualcuno potrebbe dirmi. “Sì, va bene… ma anche in  questo caso il fotone collasserebbe in particella dato che sono sicuro della sua posizione”. Avrebbe ragione se la fenditura bloccasse il fotone. Invece, lui, una volta passato crea un nuova onda la cui  “larghezza” (ossia l’angolo α) aumenta al diminuire delle dimensioni della fenditura. Più la fenditura è stretta, ossia, più è precisa la posizione del fotone, più le direzioni possibili del fotone allargano il loro spazio disponibile (l’angolo α), come abbiamo visto in Fig. 3. Ancora, in altre parole:  più è precisa la posizione del fotone e più è aleatoria la direzione che prenderà dopo il suo passaggio dalla fenditura.

Come si traduce graficamente questa situazione (non ce ne sarebbe nemmeno bisogno, ma è meglio essere rigorosi fino in fondo)? Beh… le velocità del fotone dopo il passaggio è indicata da una qualsiasi delle frecce nere di Fig. 3. Ciò che conta è l’angolo formato dai raggi “estremi” che è poi quello che deciderà la larghezza dell’immagine di diffrazione finale (ancora e sempre l’angolo α).

Come ormai sappiamo benissimo, quest’angolo aumenta al diminuire della larghezza della fenditura, ossia della precisione con cui si misura la posizione del fotone nel momento di passaggio attraverso di lei. Quale sarà l’incertezza nella sua velocità probabile? So che non abbiamo ancora parlato di vettori (tranne per coloro che hanno letto la Fisica Addormentata o che li conoscono per motivazioni personali di studio) ma è facile eseguire una semplice operazione. Separare il vettore velocità rosso in due vettori (componenti): uno diretto perpendicolarmente allo schermo finale (e alla parete) (v_y) e uno diretta lungo la parete stessa. Quest’ultimo (v_x) ci indica molto bene quanto sia grande l’incertezza della direzione della velocità del fotone.  Se v_x fosse zero la direzione sarebbe quella precedente alla fenditura, ossia lungo l’asse y. Se v_x cresce, cresce anche la possibilità del fotone di spostarsi rispetto a quella direzione. In altre parole, al crescere di v_x (e quindi al diminuire della larghezza della fenditura e all’aumentare della precisione della posizione) aumenta l’incertezza nella velocità del fotone. Più esattamente, l’incertezza nella direzione della velocità è data proprio da Δv_x = 2v_x.

Questa conclusione è in perfetto accordo con il principio di Heisenberg; Non posso conoscere perfettamente sia la posizione che la velocità di una particella. O questa o quella per me pari NON sono

La matematica ci direbbe che, “al limite”, potrei conoscere perfettamente una delle due e non avere la benché minima idea dell’altra. In realtà, la fisica non riesce ad andare "al limite" fino in fondo, come cercava di fare Zenone con la sua tartaruga. La fisica si muove a intervalli, a “pacchetti”. In un modo o nell’altro, possiamo sempre avere un’idea di entrambe le grandezze fisiche, dato che nessuna di esse può andare realmente a zero, ma a una dimensione fisicamente quantificabile. Più aumenta la precisione della prima e tanto diminuisce quella della seconda, e viceversa.

Non vi stupirete di certo, a questo punto, che possa scrivere una formuletta semplicissima che descrive sinteticamente e perfettamente il principio di Heisenberg:

Δx Δv_x ≥ h/4π

dove h non è altro che la costante di Planck, proprio quella “cosa” che ci dice che in fisica non si può andare sotto a un certo valore... Δx e Δv_x sono rispettivamente gli errori nella posizione e nella velocità. In realtà, la sua scrittura esatta sarebbe:

Δx Δq ≥ h/4π

dove, al posto della velocità, vi è la quantità di moto q della particella (la “lumaca” del mio libro sulla fisica classica, io adoro questa grandezza fisica…), ossia la massa moltiplicata per la velocità. Non ditemi che per il fotone la massa è zero e quindi la quantità di moto è zero… no… no… c’entra l’energia e la velocità della luce, ossia la quantità di moto è q = E/c. Non ne siete convinti? Uffa! Ve lo dimostro subito:

q = mv

ma, per il fotone, v = c

q = mc

ma so anche che E = mc² (lo dice il nostro amico Albert…), ossia m = E/c² e, quindi, sostituendo:

q = Ec/c² = E/c

Eh sì, sapere usare la matematica è veramente un aiuto incredibile per comprendere i fenomeni fisici.

Scusate la piccola digressione (sempre utile, comunque) e le continue ripetizioni nello spiegarvi l’esperimento legato al principio di Heisenberg. Ma, ormai, mi conoscete: preferisco battere e ribattere su un concetto, piuttosto che farvi andare avanti e indietro nell’articolo.

L’importante è di essere riusciti a esprimerlo non solo a parole, ma con dati di fatto concreti. Ormai siamo entrati nel mondo di Alice e l’illogicità comincia a essere sempre meno illogica, quasi una normalità…

Mi fermo qui… ma torneremo presto sul principio di Heisenberg e su altre applicazioni per poi arrivare all’altrettanto famoso effetto tunnel. Vorrei anche, però, riassumere e definire sempre meglio, aiutandomi con vari esempi, il significato di “informazione” in MQ. Sembra che abbia caratteristiche veramente assurde e  -a volte- contrapposte: in alcuni casi dà l’idea di poter viaggiare a velocità infinita, altre volte deve limitarsi a una sola grandezza alla volta. Vale la pena discuterci ancora un po’ sopra…

Vi consiglio questo breve, ma sorprendente, video del prof. Lewin del MIT: una prova sperimentale che spiega meglio di tante parole. Si vede benissimo come, finché la fenditura è abbastanza larga, rimanga molto indeterminata la posizione (può essere ovunque nell'apertura), mentre la velocità (ossia la direzione del movimento) sia quasi perfettamente orizzontale. Chiudendo la fenditura aumenta l'accuratezza della posizione, ma a un certo punto entra in gioco il PIH e la direzione diventa sempre più incerta.

 

Ma chi era Werner Heisenberg? Tra molte altre cose, QUI Einstein e Bohr parlano anche di lui.