Categorie: Meccanica Celeste
Tags: baricentro leggi di Keplero orbita Papalla Papalscherzone Papalterra periodo orbitale quiz
Scritto da: Vincenzo Zappalà
Commenti:23
QUIZ: Orbitando attorno alla Papalterra ***
Non si può parlare solo di matematica, di geometria e di giochi numerici ed ecco, allora, un quiz di fisica (meccanica classica), con un piccolo punto chiave. E’ ambientato su Papalla, dove sanno fare cose ancora impensabili per noi.
Su Papalla è facile costruire quello che si vuole, anche nello spazio più vuoto che c’è (con i suoi limiti, che ormai conosciamo bene). In questo caso, i papallicoli hanno costruito nientemeno che una Terra identica alla nostra, fatta, ovviamente con un materiale della giusta densità. Insomma, una bella sfera della stessa massa terrestre e delle stesse dimensioni, ricoperta da uno strato sottile di plastica che annulla ogni frizione.
Purtroppo, alcuni personaggi di Papalla hanno vissuto troppo sulla Terra e hanno cominciato a esagerare con gli scherzi. Sì, come avere già capito, sto parlando di Papalscherzone, che ha perso molte delle caratteristiche “migliori” dei suoi compagni papalliani. A forza di scherzare e di distrarsi non è stato all’altezza dell’incarico che doveva assolvere: fare in modo che il centro di gravità della nuova Terra cadesse esattamente al centro C della sfera. Insomma, non ha distribuito bene la massa al suo interno. Conclusione di questa svista: ci si è accorti che il baricentro G della sfera pseudo-terrestre era spostato di 100 km rispetto al centro. Spostamento che è risultato tutto sul piano equatoriale del pianeta posticcio.
Su Papalla si perdona in fretta, anche perché Papalscherzone ha ammesso l’errore e si è messo a disposizione per trovare una soluzione al problema.
Cosa si vuole trovare, in pratica? Nient’altro che il minimo periodo di rivoluzione di un satellite immesso in orbita equatoriale. La pseudo-Terra (chiamata Papalterra dagli indigeni) è disegnata in Fig. 1.
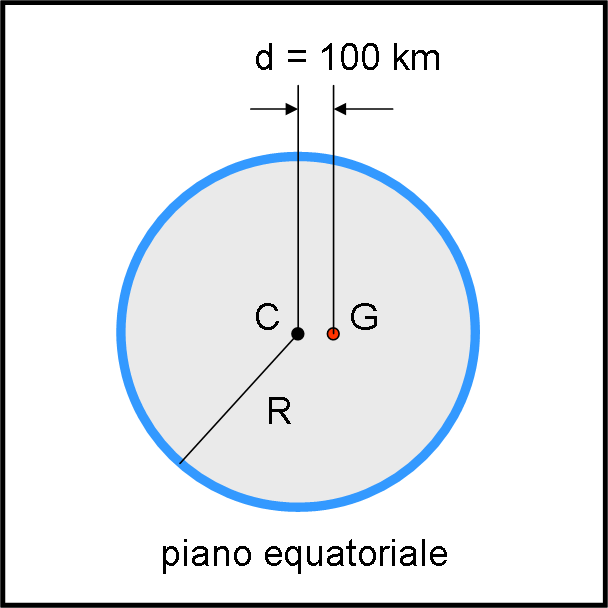
Cerchiamo di aiutare Papalscherzone a dare il risultato…
NB: Io consiglierei di fare una cosa che semplifica i calcoli: calcolare il periodo in rapporto al periodo che avrebbe un oggetto che potesse compiere un orbita circolare sfiorando la vera Terra (senza errori di Scherzy), ossia una circonferenza di raggio R. Per questo periodo si può assumere il valore di 5060 secondi.
QUI la soluzione provvisoria, QUI quella definitiva






23 commenti
Speriamo davvero che qualcuno mi aiuti... io non so da che parte cominciare!
Perché non chiedi ai tuoi colleghi papallicoli? O non ti rivolgono più la parola? Secondo me ti stai terricando un po' troppo...
Ok, glielo chiederò senz'altro, loro sì che sono gentili e disponibili!
Caro Enzo, questo Papalscherzone sembra un po' come Cimabue: una ne fa e e ne sbaglia due..
Quella che segue è una possibile soluzione, per cui invito chi ci sta ragionando a leggere dopo questo commento... tra l'altro potrei pure aver sbagliato alla grande, per cui sarebbe un po' come prender spunto da una soluzione sbagliata...
Per provare a rimediare all'errore di PapalScherzone ed evitare di cozzare contro la PapalTerra, penso sia sufficiente tener conto che il satellite deve trovarsi almeno ad una distanza dallo strano centro di gravità della PapalTerra (G) pari al raggio terrestre + 100 km.
Come mostra la figura così facendo il satellite si troverà a sfiorare il suolo in un punto della PapalTerra ed al suo punto opposto sarà ad un altezza dal suolo pari a 200 km (100 km +100 km).
Per trovare il periodo minimo di rivoluzione del satellite, si potrebbe ricavare la terza legge di Keplero.
Dunque, l'accelerazione centripeta è paria a:
ac= V²/r
Dove r è la distanza dal centro di gravità (G) e V la velocità del satellite.
L'accelerazione centripeta, però, è dovuta alla Forza di gravità:
F = G m M/r²
ma F = m a
quindi l'accelerazione dovuta alla gravità è paria a:
a = F/m = G m M/m r²= G M/r²
La massa del satellite è ininfluente...
Basta eguagliare le due relazioni trovate:
ac= V²/r
a = G M/ r²
V²/r = G M/r²
V² = G M/r
V = √G M/r
A questa velocità il satellite per compiere un giro di rivoluzione deve percorrere tutta la circonferenza, in un periodo pari a:
P = (2 π r)/V
sostituendo a V la velocità trovata prima:
P = (2 π r)/√(G M/r)
elevo entrambi al quadrato per levare di torno la radice quadrata:
P² = (2 π r)²/(√G M/r)²
P² = 4 π ² r² /G M/r
P² = 4 π ² r³ /G M
P = 2 π √(r³/G M)
Dato che:
r orbita = raggio terra + 100 km = 6 371 + 100 = 6 471 km = 6 471 x 10³ metri
G = 6,67 × 10^−11 m³/Kg s²
M = 5,972 x 10 ^24 Kg
P = 2 π √((6 471 x 10³)³/(6,67 × 10^−11 x 5,972 x 10 ^24))
P = 5182,199 secondi = 86 minuti e 22 secondi
Spero di non aver detto troppo sciocchezze...
Paolo
caro Paolo,
non hai detto sciocchezze... ma nessuno ha detto che l'orbita deve essere circolare... si può far meglio...
Io consiglierei di fare una cosa che semplifica i calcoli: calcolare il periodo in rapporto al periodo che avrebbe un oggetto che potesse compiere un orbita circolare sfiorando la vera Terra (senza errori di Scherzy), ossia una circonferenza di raggio R. Per questo periodo si può assumere il valore di 5060 secondi.
Beh...??!! Dove sono finiti i miei "prodi"????
Uno sta litigando con ellisse (sai le orbite triangolari o poligonali sono troppo spigolose), ma penso di aver trovato la soluzione...
Oggi pomeriggio non ho tempo, ma stasera penso di fare una o due figure e poi postarla... che poi sia giusta o meno si vedrà...
Paolo
Caro Enzo, ti dirò che a mio avviso quello di PapalScherzone non è stato un errore... i suoi scherzi ci costringono ad affinare continuamente i ragionamenti... lui introduce fantasiose variazioni al gioco ed apre le strade a nuovi giochi... è un vero provocatore della conoscenza.
Per cercare di rispondere al quiz ho provato a ragionare su quale orbita ellittica può garantire il minor periodo di rivoluzione.
Per costruire questa ellisse, sono partito dalla prima legge di Keplero, per cui il centro di gravità (G) deve occupare uno dei due fuochi dell'ellisse.
Il semiasse minore dell'ellisse (b) lo faccio coincidere con il raggio terrestre ed il centro dell'ellisse con il centro del pianeta (C).
In questo modo come mostra la figura, ottengo un'ellisse (con il fuoco f in G) che consente al satellite di non cozzare con il pianeta e contemporaneamente di percorrere l'orbita ellittica più breve.
Per come è stata realizzata l'ellisse, il valore del semiasse b è conosciuto, dato che coincide con il raggio terrestre e lo stesso vale per il segmento CG pari a 100 km, per cui applicando il teorema di Pitagora in un attimo si può ricavare il valore del semiasse maggiore a.
Il semiasse maggiore a non è molto più grande del raggio ed il satellite nei suoi punti più lontani (D ed E) raggiunge un altezza dal suolo di soli 784 metri (6 371 784 – 6 371 000).
Per tradurre tutto ciò in un periodo di rivoluzione del satellite posso applicare la terza legge di Keplero (quella estesa e non quella per orbite circolari), dove compare a, ossia il semiasse maggiore:
a³/P² = G (M + m)/4 π²
da cui ricavo il periodo P:
4 π²a³/G (M + m) = P²
P = √(4 π²a³/G (M + m)) = 2 π √(a³/G (M + m))
Non resta che sostituire i valori di a, G , M ed m, assegnando una massa m di 1000Kg al nostro satellite.
P = 2 π √(6 371 784³/6,67 × 10^−11 (5,972 x 10 ^24 + 1000))
P=5064 secondi
Un periodo decisamente più breve di quello trovato usando un'orbita circolare... sempre che la soluzione proposta sia corretta...
Paolo
Grazie Paolino, tu sì che mi capisci... mica come qualcun altro che mi critica sempre
caro Paolo,
la tua soluzione è decisamente interessante... e inaspettata (ammetto...). Per essere sicuri utilizziamo gli stessi numeri per non cadere in errori di approssimazione.
Rifai anche tu i calcoli, per maggiore sicurezza.
Dunque, io ho usato: raggio della Terra = 6400 km
Periodo di un oggetto che sfiori la Terra (vera) = PT = 5060 sec
A questo punto non abbiamo bisogno di altro che utilizzare la terza di Keplero:
Psat/5060 = Rapp = (a/6400)^3/2
a me viene 1.0002
Se è veramente così, la tua soluzione è migliore di quella ufficiale, che dà 1.0004!!!!
Il mio metodo era di far coincidere il perielio sul punto a destra della terra papalliana e imporre che la velocità fosse tale da non farlo penetrare nella Terra... (un metodo che avevo già visto applicare). Prima di darti un abbraccio gigantesco, controlliamo bene il risultato e che non ci stia scappando qualche errorino...
io ho calcolato la stessa ellisse di Paolo,imponendo la relazione fra distanza dal fuoco e semiasse minore uguale al raggio della terra + Pitagora,ma facendo direttamente i rapporti con la terza legge con 6371 raggio terra e 6371,784 semiasse maggiore mi viene 1,000369 come rapporto e 5060,93 come periodo.. non capisco perchè Paolo inserisca una massa per il satellite..
caro Umberto,
anch'io ho usato il rapporto e ho trovato quel 1.0002 che porta proprio a 5060.93.
Direi che è il caso di utilizzare tutti gli stessi valori dei parametri in gioco ed evitare quelli inutili. Facendo il rapporto tra i periodi si eliminano le costanti che sono inutili e possono introdurre errori...
Penso che il probelma sia legato ai dati che si usano.
Io ho usato un raggio della terra pari a 6371 km....
Così facendo, con orbita circolare ottengo un periodo di 5062,5399 secondi. e non di 5060 secondi...(tale periodo lo ottengo con un raggio molto vicino a 6400 km.
La massa del satellite l'ho aggiunta, anche se è trascurabile rispetto alla gigantesca massa dela Terra e la formula è quella che era stata ricavata qui, proprio in fondo all'articolo: http://www.infinitoteatrodelcosmo.it/2016/07/01/il-problema-dei-due-corpi-da-newton-a-keplero/
Trascurando la massa del satellite ottengo: 5063,4744 secondi.
Penso che il problema sia legato al valore da attribuire ai dati di partenza... o sbaglio?
Paolo
Ops chiedo scusa ottengo 5060 secondi con raggio pari a 6369 km...
Forse c'è qualche problema con gli altri parametri:
A G ho attribuito il valore di 6,67 x 10^-11
a M 5,972 x 10^24.
Mah..
Paolo
Penso di aver capito da dove derivano le differenze... dal valore attribuito a G ed M..
Ho affinato i due valori, migliorando la precisione, aggiungendo altri numeri:
G= 6,67408 m³/KG s²
M = 1,97219 Kg
Con raggio pari a 6371 km (orbita circolare) ottengo un periodo di 5060,911745 secondi
Con semiasse pari a 6371,748 Km ottengo un periodo paria a 5061,84595
Il rapporto dovrebbe essere di 1,00018459
Penso che le discrepanze iniziali derivino da questa approssimazione delle costanti..
Paolo
sto cercando (sono dovuto uscire...) di rifare i miei conti con gli stessi parametri vostri. Mi veniva in mente una cosa... L'ellisse che trovate è plausibile con il moto? Bisognerebbe calcolare le velocità al perielio e all'afelio... Oggi cerco di inquadrare meglio la faccenda... dato che io ho imposto la conservazione della QM e dell'energia...
Mentre Enzo esegue un po' di calcoli... posso provare a descrivere passo dopo passo quelli che ho eseguito, così se c'è un errore è più facile trovarlo..
Innanzitutto ho cercato il rapporto tra periodi, considerando prima un orbita circolare con raggio di 6371 km (raggio della Papalterra) e poi una ellittica con semiasse maggiore a di 6371,784 Km.
Non ho quindi dato per scontato il periodo di 5060 secondi... ma ho cercato di ricavarlo...
I valori di M; G e r utilizzati sono quelli indicati nella figura... la massa m del satellite non è stata considerata poiché trascurabile rispetto all'enorme massa della PapalTerra (ossia G+m ≅ G).
Per fare la prova del nove e confrontare il rapporto tra periodi con quelle tra raggio e semiasse maggiore uso la terza legge di keplero, per cui verifico i conti usando il rapporto tra il semiasse maggiore a ed r o meglio la radice quadrata del rapporto tra i lori cubi... così si levano di torno le costanti e le loro approssimazioni...
Forse così è più facile trovare errori, se ce ne sono...
Paolo
Ho un dubbio... l'orbita che trovate voi ha un senso fisico? Mi spiego... dovreste verificare se si conserva il momento angolare (seconda legge) e l'energia per due punti , ad esempio il perigeo e l'apogeo...
Quella che trovo io l'ho basata sulla conservazione...
Tra parentesi io ho usato (questa volta):
R =6371 km
e
g = 9.807 m/sec2
Il periodo dell'orbita circolare mi è risultato:
P circ = 5064.26 sec
dalla formula:
P circ = 2 pi (R/g)^1/2
Mi sa che anche questo esercizio abbia dei risvolti interessanti...
Ho un dubbio... l'orbita che trovate voi ha un senso fisico?...
penso che il problema sia questo; io di fisica ho usato ben poco, se non che l'orbita sia ellittica e che il centro di gravità della terra (che èspostato) debba occupare uno dei due fuochi; (di solito è il pianeta) il resto è solo far star dentro l'ellisse la circonferenza di raggio 6371 Km con delle identità matematiche. Non so se questa sia l'ellisse minima.
Sapete, questo quiz mi ricorda un po' il quiz delle comete suicide, in cui era il sistema solare a spostare il suo centro..
domattina cerco di scrivere il metodo usato da me (oggi non ce l'ho fatta...) e poi vediamo se si scopre il punto chiave...
Io ho un dubbio su come affrontare questo problema.
Questa pseudo-Terra non è a simmetria sferica ed il satellite è molto vicino alla superficie.
E' lecito ragionare su questo caso in base alle leggi di Keplero e/o posizionando la massa nel centro di massa senza considerare l'effettiva distribuzione delle masse?
caro Fabry,
il centro di massa rimane comunque il punto dove puoi concentrare tutta la massa, su questo non ci sono problemi. Il problema è che bisogna impartire una velocità iniziale al satellite in modo che rimanga in orbita. Io ho cercato di trovare la minima in assoluto... e non solo di costruire un'ellissi attorno a un cerchio...
Se riesco stamattina finisco i conti, più lunghi del previsto e poi ne discuteremo ancora...
caro Fabry,
mi spiego meglio (sono stato troppo sbrigativo). Capisco benissimo cosa intendi dire tu (variazioni di densità locali e cose del genere). Per non creare problemi supplementari immaginiamo che la distribuzione sia omogenea e che la differenza tra baricentro e centro non influisca sul movimento "locale" del satellite...