QUIZ: eleviamoci a noi stessi… ****

29/10/16

QUIZ: eleviamoci a noi stessi… ****

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:7

Questo esercizio è di pura matematica e necessita di una certa esperienza e intuizione. Insomma, è un po’ cattivello… ma sono convinto che qualcuno mi stupirà…

Quali sono le soluzioni della seguente equazione:

xx = 1/√2

Mi accontento di due soluzioni, molto evidenti (ma non andate per tentativi!).

Chi vuole può anche dimostrare che esse sono, in realtà, solo due.

Articoli correlati

7 commenti

  1. Paolo
    29/10/2016 at 19:26

    Caro Enzo, che dire, io ci provo, poi si vedrà...

    Dunque, elevo entrambi i membri al quadrato:

    x^x = 1/√2

    (x^x)² = (1/√2)²

    x^2x = ½

    è del tutto evidente che se x=½, si ottiene:

    ½^2 1/2 = ½

    ½^1 = ½

    quindi la prima soluzione dovrebbe essere x=1/2

    la seconda mi sembra piuttosto simile, assumendo che x = 1/4:

    1/4^2  1/4 = ½

    1/4^1/2 = ½

    ½ = ½

    quindi la seconda soluzione dovrebbe essere x= ¼

    Sembra funzionare.. :roll: 

    Paolo

  2. Arturo Lorenzo
    29/10/2016 at 19:57

    Ottimo, Paolo.

    Aggiungo solo che le soluzioni , che sono quelle indicate, possono essere solo quelle due. Infatti, facendo lo studio della funzione

    y=x^{x}

    e disegnandone il grafico, si ottiene che:

    • la funzione è definita in R+ meno  lo zero
    • per x tendente  a zero da destra, il limite della funzione è pari a 1
    • la funzione attinge un solo valore minimo (per x= 1/e = 0,368),  pari a 0,692
    • per x tendente a + infinito, il limite della funzione è + infinito

    Quindi, la retta di equazione

    y=\frac{1}{\sqrt{2}}

    cioè y=0,707 , che sta sopra pertanto il suddetto punto di minimo della funzione,  non può  che intersecarne il grafico solo in due punti, le cui ascisse sono appunto 1/2 e 1/4.

     

     

     

     

  3. Vincenzo Zappalà
    30/10/2016 at 05:31

    Bene ragazzi... avete superato un "doppio" quiz! Siete riusciti a non farvi trascinare dall'esponente verso soluzioni logaritmiche (che sarebbe la via normale e più ovvia) e avete mirato al sodo.  Beh... che dirvi... non ho più parole, mi avete stupito ancora una volta e non era facile, conoscendovi già. Poi vi darò la soluzione "canonica" che dimostra come la fantasia, senza paura e legata a solide basi, può essere libera di agire senza preconcetti.

    :-P :-P  :-P  :-P

  4. Umberto
    30/10/2016 at 06:30

    Volevo osservare che  però è necessario eseguire una sostituzione logaritmica per dimostrare che la derivata si annulla in un solo punto (1/e) e che quindi le soluzioni sono solo solo due, come dice giustamente Arturo; senza la sostituzione f(x)=x^{x}=e^{\ln(x^{x})} =e^{x\cdot \ln x} non riusciamo a calcolare la derivata di f(x), f'(x)=e^{x\cdot \ln x}D(x\cdot \ln x)=e^{x\cdot \ln x}\cdot (1\cdot \ln+x\cdot 1/x)=e^{x\cdot \ln x}(\ln x+1)

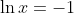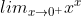    questa si  annulla se e solo se si annulla (\ln x+1) ovvero  \ln x=-1, e visto che la base di ln è e, x=1/e. Allo stesso modo, senza l'espressione f(x)=x^{x}=e^{\ln(x^{x})} =e^{x\cdot \ln x} non sarebbe tanto facile dimostrare che lim_{x \to 0^{+}}x^{x}=1,  mentre invece ci basta provare che 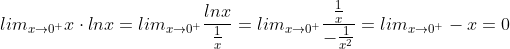lim _{x \to 0^{+}} x\cdot ln x=lim _{x \to 0^{+}}\frac{lnx}{\frac{1}{x}}=lim _{x \to 0^{+}}\frac{\frac{1}{x}}{-\frac{1}{x^{2}}}=lim _{x \to 0^{+}}-x=0( al terzo passaggio abbiamo fatto la derivata di numeratore e denominatore applicando la regola di de l'Hopital).  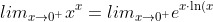quindi lim_{x \to 0^{+}}x^{x}=lim_{x \to 0^{+}} e^{x\cdot \ln(x)}=e^{0}=1

     

  5. Vincenzo Zappalà
    30/10/2016 at 06:43

    grazie Umberto... hai messo la ciliegina sulla torta! :-P

    Per voi ci vorrebbero quiz ben più elevati... :roll:

  6. AlexanderG
    16/11/2016 at 16:06

    Ciao!

    Ogni tanto trovo il tempo di seguire questo bellissimo blog, e perfino di divertirmi a cercare le soluzioni di questi divertenti quiz :)

    Allora, non ho visto la soluzione, il mio ragionamento è il seguente:

    x^{x}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}=\frac{2^{\frac{1}{2}}}{4^{\frac{1}{2}}}=\left ( \frac{1}{2} \right )^{\frac{1}{2}}

    Quindi una soluzione è sicuramente: x=1/2=0.5

    Allo stesso modo:

    x^{x}=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt[4]{4}}=\left ( \frac{1}{4} \right )^{\frac{1}{4}}

    Pertanto la seconda soluzione è: x= 1/4=0.25

     

    Un caloroso abbraccio a tutti, in particolar modo al grande Enzo :)

  7. Vincenzo Zappalà
    16/11/2016 at 18:38

    grazie a te Alex!!!!

    Sentivo al tua mancanza....

    Tutto giusto, ovviamente!

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.