Abbiamo discusso a lungo della curvatura di curvatura di uno spazio a due dimensioni e abbiamo visto come la geometria che lo descrive si discosti completamente da quella euclidea che impariamo a scuola. Come detto varie volte, la curvatura di uno spazio (lasciando da parte il tempo, almeno per adesso) è legata strettamente alla relatività generale, un argomento che aspetta ancora di essere affrontato in modo diretto e decisivo. Vale la pena capire ancora meglio cosa si intende per “curvatura”

Ho letto varie “divulgazioni” della relatività ristretta e di quella generale che tutto fanno fuorché spiegare, anzi inducono errori fondamentali che poi sono difficili da estirpare. Questo è il motivo per cui voglio preparare per bene l’argomento degli argomenti, quello su cui si basa gran parte della astrofisica macroscopica, non ultima la creazione delle onde gravitazionali.

Vi preannuncio già che vi sono vari metodi per arrivare al dunque, tra cui quello seguito da Einstein, che è forse il più disordinato e saltellante. D’altra parte, sapendo il risultato è sempre possibile migliorare il procedimento logico. Il merito, tuttavia, va solo e soltanto a chi, in qualsiasi modo ci sia arrivato, è giunto per primo alla soluzione delle soluzioni, utilizzando solo l’intuizione di una mente superiore.

Accettiamo, quindi, alcuni articoli che sembrano distanti dal nocciolo del problema e che, invece, preparano la mente ad affrontare certe conclusioni che solo un genio poteva non solo descrivere, ma anche solo immaginare.

Questa volta parliamo di una “falsa” curvatura, ossia dimostriamo come certe caratteristiche che abbiamo compreso con qualche difficoltà su una superficie sferica, possano essere riprodotte perfettamente su una superficie piana, agendo su altre caratteristiche fisiche.

Lo scopo è quello di far capire che parlare di curvatura dello spaziotempo non è un qualcosa che debba subito far pensare a una superficie o addirittura a uno spazio realmente curvo, ma solo a un qualcosa che permetta di considerare come linea di minima distanza (geodetica) una traiettoria non rettilinea. Insomma c’è curvatura e curvatura, ma non facciamoci ingannare dalla “parola” in sé e pensiamo al concetto ben più generale.

Non commettiamo lo stesso errore che si fa parlando di forma dell’Universo, immaginandosi veramente una struttura con una forma a sfera, a sella o completamente piatta. Quello che conta è la geometria che descrive un qualcosa e nel caso della curvatura legata alla relatività generale una geometria del tutto identica a quella esistente su una superficie sferica, ma senza per forza pensare a una vera superficie curva…

Spero di aver chiarito le idee e non di averle confuse. Meglio passare a un esempio che, guarda caso, ho -ancora una volta- sviluppato rifacendomi a quel pozzo di scienza divulgativa che è Feynman.

Dimentichiamoci, perciò, la superficie sferica (tenendo ben presente però le conclusioni che abbiamo ricavato) e mettiamoci su un piano che più piano non si può. Un  piano apparentemente piano, ma in cui le condizioni fisiche sono ben diverse!

Prendiamo un punto qualsiasi del piano. Diamo sufficiente spazio attorno al punto in tutte le direzioni (consideriamolo pure al centro, anche se parlare di centro di un qualcosa di indefinito spazialmente è sempre privo di senso). Adesso, immaginiamo che il nostro piano diventi una specie di piastra per cuocere i cibi, però … al contrario. Mi spiego meglio. Il punto centrale è quello in cui la temperatura è minima, mentre a mano a mano che ci allontaniamo, la temperatura sale con una certa legge, che, al momento ci interessa ben poco.

Possiamo anche pensare che uno spazio piatto, veramente piatto a prima vista, abbia una certa capacità di far variare la “temperatura” a distanze crescenti da un certo punto, che possiamo identificare con un oggetto dotato di una certa massa. Una massa capace, in qualche modo, di fornire calore tutt’attorno. Una specie di fornello al contrario. Il calore è, però, solo un esempio. L’importante è che causi una qualche legge che agisca sullo spazio circostante e sui suoi strumenti di misura.

Fatemi disegnare la Fig. 1 che riesce sicuramente a spiegare la faccenda meglio che tante parole. Ogni cerchio attorno al punto-massa -o quello che volete- ha una temperatura crescente verso l’esterno. Per misurare le distanze su questa strana “piastra”, dobbiamo usare un righello di distanza unitaria (sappiamo quanto importanti siano i righelli della relatività ristretta… QUI, Fig. 14).

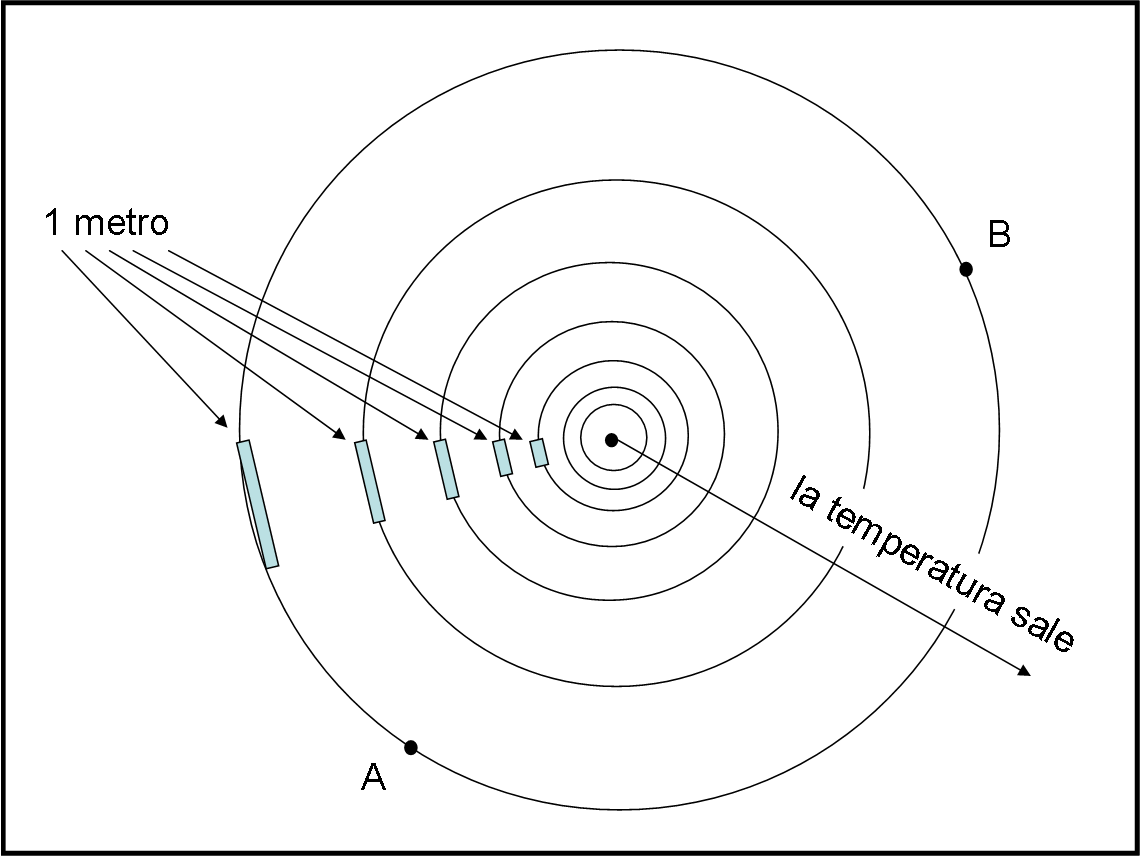
Purtroppo, però, il materiale di cui è composto il righello è sensibile alla temperatura e le sue dimensioni si dilatano in funzione di essa. Il che vuole anche dire che qualsiasi oggetto di quel materiale venga posto sulla piastra è costretto a dilatarsi seguendo le regole del gioco. Ricordiamo sempre bene che la dilatazione o contrazione non è la stessa da punto a punto, ma è funzione della distanza dal centro.

Nella figura, sulla sinistra, abbiamo disegnato i righelli unitari relativi a varie temperature crescenti dal centro verso l’esterno. Attenzione: li abbiamo disegnati, ma verranno tolti quando si passerà alla prova vera e propria.

Immaginiamoci adesso una scuola aliena, dove si stanno interrogando alcuni studenti. E’ una prova impegnativa, estremamente importante per il futuro scolastico. Ciò che si deve fare è andare su quello strano mondo, che gli studenti non conoscono, ed eseguire una certa misura con un righello di misura unitaria (un metro). Viene mandato per primo uno studente abbastanza “normale”.  Il giovane non è “piatto” e vede, perciò, chiaramente che il mondo raggiunto è veramente piatto anche estrinsecamente. Purtroppo, gli alieni non possono sentire il caldo e il freddo, dato che questo senso non fa parte della loro dotazione sensoriale… Tuttavia, sono “fatti” dello stesso materiale dei righelli che hanno a disposizione. Nel loro mondo la temperatura è sempre perfettamente costante…

Il compito che gli è stato dato è quello di trovare la minima distanza tra due punti A e B. “Banale!” pensa lo studente. Lo spazio è piano e non deve fare altro che prendere il suo righello e vedere quante volte è contenuto nel segmento AB. Geometricamente non ha sbagliato niente, tranne il non aver tenuto conto dell’espansione o della contrazione del suo righello (che non può notare dato che anche lui -il piccolo alieno- è fatto dello stesso materiale del righello).

Tracciamo il segmento AB nella Fig. 2.

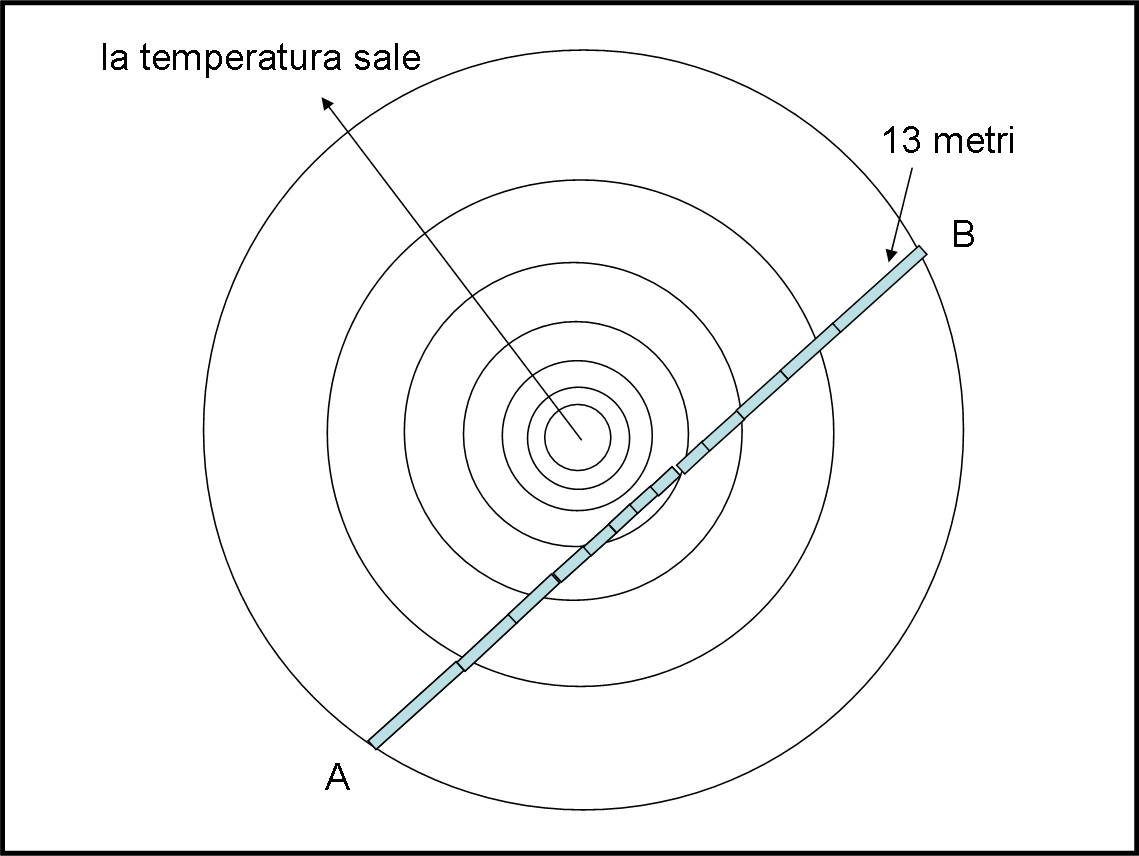
Si vede chiaramente che il segmento attraversa cerchi concentrici con temperatura sempre inferiore fino a un minimo e poi ricomincia a tornare verso zone a temperature più alte. Per metterlo in maggiore difficoltà A e B sono stati scelti alla stessa distanza dal centro, in modo che la temperatura di partenza sia uguale alla temperatura di arrivo.

Mentre il nostro amico sistema il righello, la lunghezza di quest’ultimo diminuisce fino a raggiungere un valore minimo dove la temperatura è più bassa e poi ricomincia a salire fino a tornare alle identiche dimensioni della partenza. In questo modo anche un osservatore esterno (amico dello studente) potrebbe misurare il righello all’inizio e alla fine e potrebbe dire che nulla è cambiato. Povero studente e povero amico controllore…

Torna al suo mondo dando come distanza minima un valore del tutto sbagliato! Lui dice con grande sicurezza: “La minima distanza tra A e B è 13 metri. Il mio righello è stato contenuto esattamente tredici volte tra A e B”. E viene bocciato!

La Fig. 2 illustra cosa è realmente successo. Il righello varia la sua lunghezza in base alla temperatura e, a mano a mano che lo studente misura, il suo strumento si fa più piccolo per poi aumentare di nuovo. 13 metri è una distanza enormemente più grande della realtà di quello strano mondo.

La Fig. 3 illustra un altro tentativo fatto da un compagno ritenuto il migliore della classe (un vero sgobbone, senza troppo intuito, però).

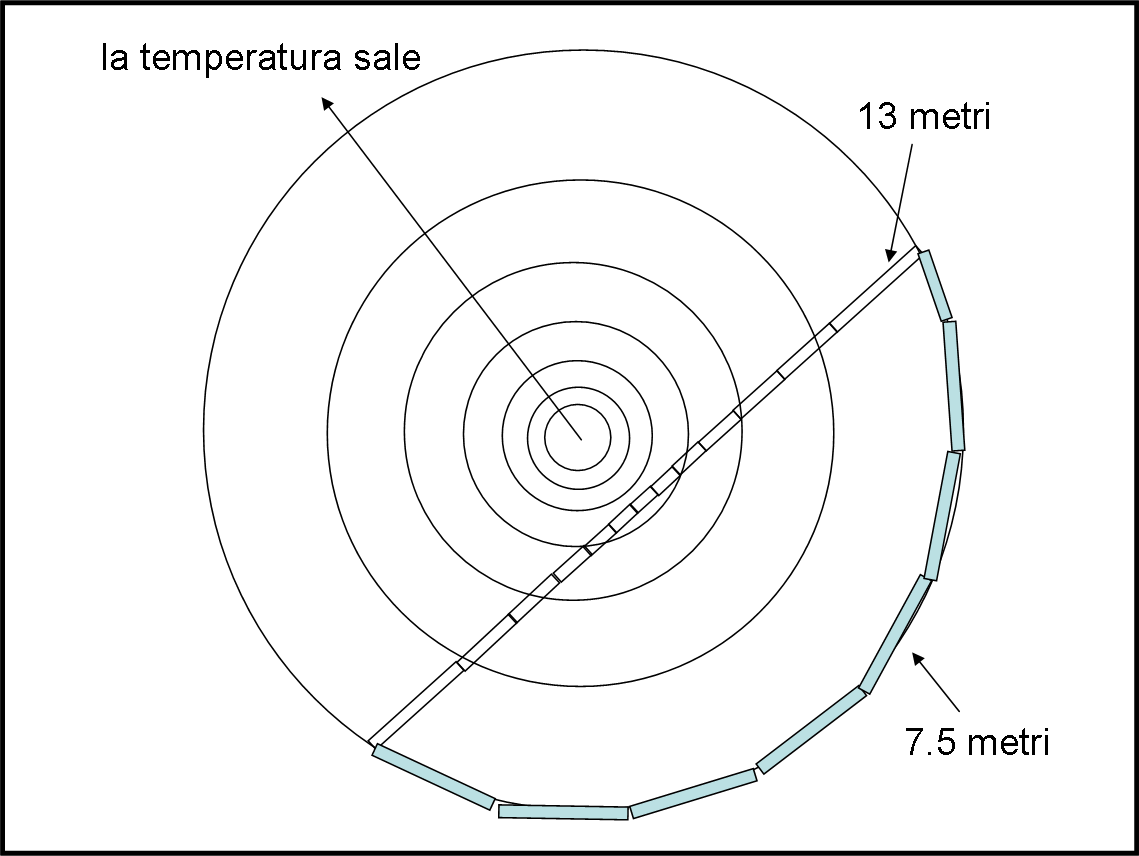
Lui sa tutto sui cerchi massimi di una superficie sferica, però non capisce che cosa c’entrano con un piano visto come tale anche in modo estrinseco. Tuttavia, è abituato a lavorare un po’ alla “io speriamo che me la cavo”, anche senza sapere il perché. Inizia a mettere i righelli lungo la circonferenza che passa da A e da B e, in realtà, trova una distanza nettamente minore: 7.5 metri!

Tutto contento torna a scuola, ma, questa volta, è costretto a subire una delusione: sì, il suo valore e migliore di quello del primo studente, ma non è ancora quello giusto.

Un terzo studente ci ragiona sopra e trova del tutto inconcludente seguire una circonferenza che non sarebbe né carne né pesce.  Valutando i risultati di chi l’ha preceduto, ha un lampo di genio (lui è abituato a queste intuizioni, ma la scuola è rigida e preferisce che si seguano regole ben stabilite senza dare molto spazio alla fantasia, anche se basata su una logica ineccepibile).

Fa qualche calcolo e capisce che il percorso minimo dipende sia dalla distanza percorsa in modo rettilineo (il piano resta un piano), ma anche dalla distanza dal centro. Se passasse troppo vicino a questo il numero di righelli da usare aumenterebbe troppo (vincerebbe la contrazione). Se andasse oltre la circonferenza di A e B, guadagnerebbe in termini di lunghezza del righello, ma perderebbe in distanza lineare. Ci vuole un giusto compromesso.

Ancora qualche calcoletto e poi alza la mano, proponendosi per un nuovo tentativo. I professori si guardano tra loro, alquanto dubbiosi, però non possono negargli la prova. Il terzo studente scende sullo strano mondo piatto e segue una traiettoria sicuramente curva ma che dona un risultato di soli 6 metri, come mostra la Fig. 4.

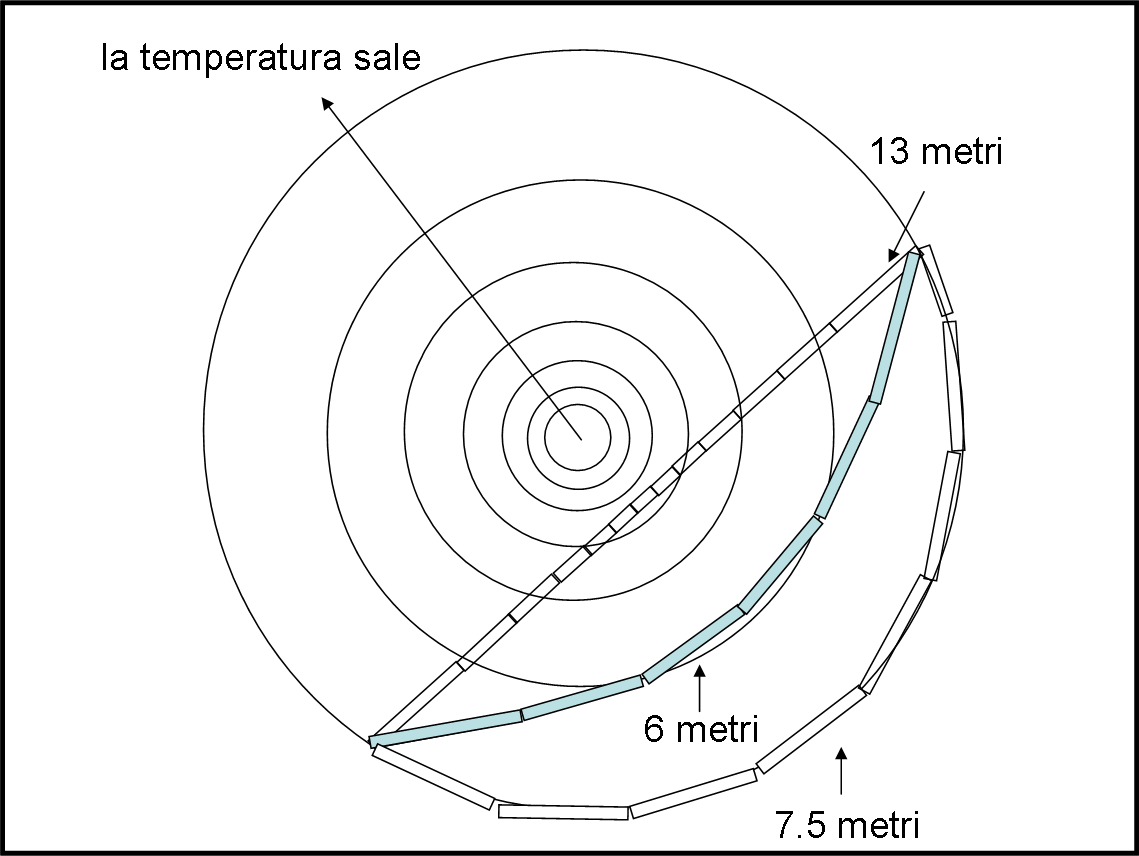
La sua gioia si ingigantisce (come il righello) mentre guarda  la bocca aperta dei professori che, d’ora in poi, lo vedranno con occhi diversi.

In poche parole, la legge con cui il righello si allunga con la temperatura è una proprietà fondamentale di quel mondo piatto e impone un percorso di minima distanza, che tutto è fuorché una linea conforme all’aspetto geometrico apparente. Una proprietà che viene evidenziata dalla presenza della massa-piastra.

La morale della storia è che una massa dotata di proprietà “speciali” (la stessa massa, in realtà) è capace di deformare lo spazio intorno a lei in modo che le distanze minime non siano più linee.

Tradotto in parole ancora più semplici ed esplicative: una massa è capace di variare la lunghezza dei righelli a seconda della loro distanza rispetto a lei. Sappiamo, però, che lo spazio è in pratica un qualcosa definito dai righelli (ricordatevi lo studente Einstein durante il suo confronto con lo studente Newton… QUI, Fig. 14). In conclusione: una massa è capace di deformare lo spazio, dove per deformare si intende qualcosa di ben più generale che la curvatura di una superficie sferica. In questo contesto, la minima distanza segue regole del tutto particolari.

Spero di aver fornito una chiave in più per aprire con accuratezza la porta della Relatività Generale. Quando sarà il momento, metteremo di nuovo in evidenza questa piccola avventura aliena.

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI trovate l'approfondimento dedicato alla Relatività Generale