Categorie: Matematica Meccanica Celeste
Tags: Papalterra periodo minore quiz satellite artificiale soluzione
Scritto da: Umberto Cibien
Commenti:1
Soluzione definiva (!) dell'orbita attorno a Papalterra (di Fabrizio e Umberto) ***
Questo articolo mostra la soluzione definitiva del problema dell'orbita minore possibile di un satellite artificiale, attorno alla Papalterra, una Terra con il centro di gravità spostato rispetto al centro geometrico. Tutte le informazioni e un paio di soluzioni si trovano QUI e QUI. In un successivo articolo (QUI) proponevo un metodo generale che portasse alla soluzione.
Fabrizio e Umberto lo hanno affrontato di petto e sono giunti alla conclusione. Nessuna delle soluzioni precedenti era la migliore... Devo dire che hanno fatto un lavoro encomiabile e decisamente laborioso dal punto di vista dei passaggi algebrici. Non hanno desistito e hanno trovato lo stesso risultato! Congratuliamoci vivamente con loro, una risorsa fondamentale di questo Circolo.
Il problema è stato impostato così:
Si è considerato un punto generico O (che stia sull'asse congiungente baricentro e centro di Papalterra) come centro dell'ellissi.
Si scrive , perciò l'equazione dell'ellisse generica che abbia centro in O e fuoco in G, e poi quella del cerchio di raggio R con centro in C. Si ponga come variabile fondamentale:
c = OC
La condizione fondamentale è che cerchio ed ellissi siano tangenti (ossia non si intersechino e si tocchino in solo due punti). In tal modo si ottiene l'equazione a = f(c) e si cerca il valore di c che dia il minimo semiasse (minimo semiasse vuol dire minimo periodo di rivoluzione). Un perfetto studio di funzione (da costruire) e di applicazione della derivata di un qualcosa non molto semplice.
La figura base è quella che segue:
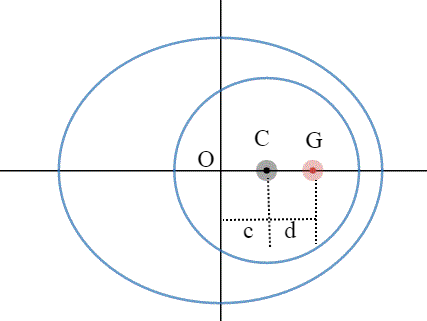
La distanza OC, come già detto, è indicata con c, mentre d è la distanza (nota) tra il centro del pianeta e il centro di gravità.
Equazione circonferenza con centro in C:
equazione canonica dell'ellisse con centro negli assi:
ponendo c+d=e, si ha:
, (attenzione: questa e non ha niente a che vedere con l'eccentricità!)
queste sono tutte le possibili ellissi con fuoco in G.
Ricordiamo che un orbita ellittica è possibile se il centro di gravità G coincide con il fuoco dell'ellisse. E questo è stato adeguatamente tenuto in conto.
Limitiamoci al semipiano positivo delle y (possiamo farlo per questioni di simmetria); affinché la semi-ellisse contenga la semi-circonferenza, deve essere:
questa è una parabola rivolta verso l'alto (il coefficiente di è positivo) ; studiamo il discriminante:
; ponendo
(in tal modo essendo la parabola rivolta verso l'alto e l'intersezione con l'asse delle x unica, essa risulta sempre >=0 )e sostituendo a e=c+d; otteniamo una espressione per a (semiasse maggiore) in funzione di c;
moltiplichiamo per :
Calcolandola per un valore utilizzato in passato (c = 0), si ottiene il risultato voluto, che però non è il valore relativo al minimo valore di a, come si dimostrerà tra poco.
Forse, alcuni passaggi precedenti non sono chiarissimi a tutti (Umberto è decisamente un matematico "puro" e rigoroso!), e mi permetto di inserire i passaggi che ho svolto personalmente, che danno, ovviamente lo stesso risultato:
Consideriamo come origine il centro dell’ellissi generica.
La figura è quella precedente di Umberto
x2/a2 + y2/b2 = 1
sappiamo anche però che:
OG = c + d
Da cui:
b2 = a2 – (c + d)2
Ponendo e = c + d
Si ha:
b2 = a2 – e2
da cui:
x2/a2 + y2/(a2 – e2) = 1 …. (1)
La circonferenza di centro C (OC = c) ha equazione:
(x – c)2 + y2 = R2 …. (2)
Facendo sistema tra (1) e (2) trovo le intersezioni tra ellissi e circonferenza
(x – c)2 + y2 = R2
x2/a2 + y2/(a2 – e2) = 1
Ricavo y2 dalla prima e lo sostituisco nella seconda:
y2 = R2 – (x-c)2
x2/a2 + (R2 – (x-c)2 )/(a2 – e2) = 1
questa è l’equazione che ci deve dare le ascisse delle intersezioni, se esistono, tra ellissi e cerchio.
Svolgiamola per bene:
x2(a2 – e2) + a2(R2 – (x-c)2) = a2(a2 – e2)
x2a2 – x2 e2 + a2R2 – a2x2 - a2c2 + 2a2xc - a4 + a2e2 = 0
semplificando x2a2
si ottiene:
- e2x2 + 2 a2xc + a2R2 - a2c2 - a4 + a2e2 = 0
Cambiamo di segno:
e2x2 - 2 a2xc - a2R2 + a2c2 + a4 - a2e2 = 0
A noi interessa solo il caso in cui le due curve siano tangenti, ossia che la soluzione sia unica. Questo si ottiene ponendo uguale a zero il discriminante di un’equazione di secondo grado ridotta:
a4c2 – e2(- a2R2 + a2c2 + a4 - a2e2 ) = 0
a4c2 + e2a2R2 – e2a2c2 –a4e2 + a2e4 = 0
a2(a2c2 + e2R2 – e2c2 – a2e2 + e4) = 0
a non può essere uguale a zero, quindi:
a2c2 + e2R2 – e2c2 – a2e2 + e4 = 0
e è funzione di c e d, d è noto, R è noto. La funzione precedente vede a come funzione della sola c.
a2(c2 – e2) = e2c2 – e2R2 –e4
La funzione va esplicitata in a:
a2 = (e2c2 – e2R2 – e4)/( c2 – e2)
a = e ((c2 –R2 – e2)/(c2 – e2))1/2
Prendiamo solo il segno più dato che a deve essere positiva
Poniamo, finalmente, (c + d) al posto di e
a = (c + d)((c2 – R2 – (c + d)2)/(c2 – (c + d)2)1/2
a = (c + d)((c2 – R2 – c2 – d2 – 2dc)/(c2 – c2 – d2 – 2dc))1/2
a = (c + d)((R2 + d2 + 2dc)/(d2 + 2dc))1/2
Questa sarebbe la funzione di cui si deve trovare il minimo…
Ovviamente, per
c = 0
vale a = (R2 + d2)1/2
Prendiamo la soluzione riportata nei commenti da Fabrizio:
a = (c + d) (1 + R2/(d(2c + d)))1/2
e la sviluppiamo
a = (c + d) ((d(2c + d) + R2)/(d(2c +d))1/2
a = (c + d) ((2dc + d2 + R2)/(2dc + d2))1/2
Che è perfettamente il risultato precedente…
La prima parte è completata: abbiamo la funzione di cui dobbiamo trovare il minimo. Essa è proprio del tipo:
a = f(c) (tutti gli altri parametri sono noti)
Per facilitare i calcoli poniamo c = x e la faccenda diventa più... "normale".
Seguiamo, adesso, il procedimento di Umberto che porta allo stesso risultato di Fabrizio:
Deve essere, ovviamente: ovvero
il numeratore è positivo per
ovvero
,
il denominatore è positivo per , il segno del rapporto sarà negativo quando i segni sono diversi, quindi in
la funzione non è definita
scriviamo la funzione come Fabrizio , dividendo per d(2x+d):
(derivata di un prodotto)
poniamo Da(x)=0
che porta all'equazione di 2° grado:
Calcoliamo prima il discriminante:
poi le radici:
Osserviamo che per x = c=0, la derivata non si annulla, quindi non è il minimo cercato.
La prima radice , è:
proviamo a vedere
che è vero, quindi la scartiamo
consideriamo la seconda soluzione e vediamo se
che è vero .
Quindi, questa è la soluzione da prendere, ed è un minimo per la funzione a(x)
calcoliamo (x2+d) e (2x2+d)
Chi ha voglia può divertirsi a disegnarla e a trovare la posizione del perigeo, ma pensiamo si sia già lavorato abbastanza...






1 commento
Complimenti per la tenacia! Bravi!