Matematiche pure 4) :Altri esempi di gruppi **/***

19/11/16

Matematiche pure 4) :Altri esempi di gruppi **/***

Categorie: Matematica Tags: Scritto da: Umberto Cibien Commenti:0

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Proseguiamo lo  studio dei gruppi, analizzando due gruppi fondamentali costruiti su Z; Le classi di resto modulo n (un valido esempio anche per approfondire il concetto di equivalenza) e il gruppo prodotto. Poi la verifica del fatto che anche le trasformazioni di Lorentz formano un gruppo,che era stato proposta ai lettori nell'articolo precedente.

Le classi di resto modulo n: \mathbb{Z}_{n}.

Nell'insieme Z dei relativi, consideriamo la seguente relazione di equivalenza( le relazioni di equivalenza le abbiamo viste qui):

a\sim b : a è equivalente a b se  a,b danno lo stesso resto divisi per un certo n fissato.

Ricordiamo che la divisione fra interi è la soluzione di un problema; dati a ,n,dividere a per n equivale a  trovare  due interi  q,r tali che a=nq+r con r<n. Vogliamo trovare un altro metodo per esprimere questa relazione. Sia ad esempio n=3; siano a,b due numeri interi.

a=3x+r1

b=3y+r2

supponiamo che a,b abbaino lo stesso resto; allora r1=r2

a-b=3x-3y+r1-r2=3(x-y); quindi per essere equivalenti la loro differenza deve essere multiplo di 3. Abbiamo trovato un modo più comodo per verificare se due elementi sono equivalenti.

verifichiamo le tre proprietà che caratterizzano le relazioni di equivalenza:

proprietà riflessiva:  a\sim a,  essendo a-a=0 e quindi multiplo di 3

proprietà simmetrica: se a\sim b , a-b=3m, b-a=-3m quindi b\sim a

proprietà transitiva:sea\sim b  allora a-b=3m, se   b\sim c allora  b-c=3n

ma allora a-c=b+3m +3n-b=3(m-n) , quindi a\sim c

Lo stesso vale per n generico. Quindi  essendo \sim una relazione di equivalenza, possiamo considerare l'insieme quoziente, ovvero l'insieme delle classi di equivalenza.Ricordiamo che le classi di equivalenza costituiscono una partizione dell'insieme (in questo caso Z).Per rappresentare una classe,possiamo prendere uno qualsiasi dei suoi elementi come rappresentante. Nel caso n=3 possiamo considerare come rappresentanti i numeri 0,1,2 che altro non sono che i resti possibili. Infatti 0 diviso 3 dà quoziente 0 e resto 0, 1 diviso 3 dà quoziente 0 e resto 1, 2 diviso 3 dà quoziente 0 e resto 2

Z è unione delle classi [0],[1],[2], che sono disgiunte, essendo una partizione .

Per n generico avremo 0,1,2,..n-1, quindi n classi. Indichiamo con \mathbb{Z}_{n} tale insieme quoziente. Più precisamente l'insieme quoziente è costituito dalle classi \mathbb{Z}_{n}={ [0],[1],[2],[3],   ...[n-1]}.

Per n=3, 0,1,2,3 non sono altro che dei rappresentanti delle classi. Per esempio la classe [1] ha come elementi 1,4,7,10,.)  ma non dimentichiamoci anche i numeri negativi(..,-11, -8, -5, -2).Infatti tutti divisi per 3 danno resto 1.

Nell'insieme quoziente, per definire un gruppo dobbiamo definire una operazione interna, ovvero una corrispondenza di \mathbb{Z}_{n} x \mathbb{Z}_{n}--->\mathbb{Z}_{n}

Definiamo la somma fra due elementi [ a ] e [b ] come la classe  del resto della divisione di  a+b per n.Tale operazione così definita è interna; infatti tornando all'esempio n=3, il resto di a+b (diviso per 3) qualsiasi siano a,b è sempre un numero minore di 3, che quindi appartiene ad una delle classi [0],[1],[2],[3]; è una buona definizione,ovvero è sensata, in quanto non dipende da quali rappresentanti scegliamo per le classi  di a,b.

Supponiamo per esempio (caso n=3) [1]+[2]=[1+2]=[3]=[0]; se cambiamo rappresentanti [4]+[5]=[4+5]=[9]=[0].

In generale,   [a]+[b]=[a+b]; se a\sim a',b\sim b' , [a']+[b']=[a'+b'] ma a-a'=kn, b-b'=zn, a+b=a'+kn+b'+zn=a'+b' + n(k+z), a+b-(a'+b')=n(k+z) quindi per la definizione dell'equivalenza  [a+b]=[a'+b'].

Verifichiamo le tre condizioni per fare di \mathbb{Z}_{n}un gruppo. La proprietà associativa deriva immediatamente dalla proprietà associativa di Z; se facciamo infatti

( [a]+[b]) +[c]=[a+b] +[c]=[(a+b)+c]=[a+(b+c)]= [a]+([b] +[c])

Qualsiasi sia [a], l'elemento neutro è la classe [0]; infatti  [a] +[0]=[a+0]=[a]; l'inverso di [a] è la classe di [-a], infatti [a]+[-a]=[a-a]=[0].

L'operazione    è poi commutativa : [a]+[b]=[a+b]=[b+a]=[b]+[a] quindi \mathbb{Z}_{n} è un gruppo abeliano

Il gruppo Z x Z

Z x Z con la seguente operazione interna (a,b)+(c,d)=(a+c,b+d) è gruppo.

0)Proprietà associativa:

[(a,b)+(c,d)]+(e,f)=(a,b)+[(c,d)+(e,f)]

Potete intuirlo immediatamente dal fatto che su Z  l'operazione di somma è associativa. infatti [(a,b)+(c,d)]+(e,f)=(a+c,b+d) +(e,f)=(a+c+e,b+d+f)=

(a,b)+(c+e,d+f)=(a,b)+[(c,d)+(e,f)].

1) Chiusura rispetto all'operazione interna: (a,b)∈ Z x Z, (c,d)∈ ZxZ => (a+c,b+d)∈ Z x Z

perché Z è gruppo additivo , come tale è chiuso rispetto all’ addizione , cioè sulla prima componente si ha a∈Z, c∈Z =>a+c∈Z e idem sulla seconda componente b∈Z, d∈Z =>b+d∈Z
2)esistenza dell'elemento neutro; cerchiamo una coppia  (e1,e2) tale che, qualsiasi siano a,b si abbia (a,b)+ (e1,e2) =((e1,e2) +(a,b)=(a,b)
basta prendere  (e1,e2)=(0,0)

z-x-z
la somma così definita in Z x Z non è altro che una somma di vettori,operando sulle componenti; sappiamo che per essi vale la proprietà associativa, l'elemento neuro è il vettore di lunghezza nulla, e sappiamo che ogni elemento ha un opposto

3) Inverso; qualsiasi sia l'elemento (a,b) di Z x Z se consideriamo (-a,-b) si ha:

(a,b)+(-a,-b)=(-a,-b)+(a,b)=(0,0)

L'operazione è poi commutativa: (a,b)+(c,d)=(a+c,b+d)=(c+a,d+b)=(c,d)+(a,b).

Il gruppo delle trasformazioni di Lorentz

Da un  punto di vista strettamente matematico, le trasformazioni di Lorentz sono delle funzioni di R x R--->R x R che associano ad una coppia (x,t) la coppia (x',t') con la seguente legge:

1)\left\{\begin{matrix} x'=\gamma (v)(x-vt))\\ t'=\gamma (v)(t-\frac{v}{c^{2}}x) \end{matrix}\right.

dove \gamma (v)=\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} è un parametro che dipende dalla sola velocità v, velocità relativa fra i due sistemi. Quindi chiamando  L 'insieme delle trasformazioni di Lorentz in uno spaziotempo bidimensionale, esse dipendono da un solo parametro, v;L={\lambda _{v}}. Possiamo dunque scrivere \lambda _{v}:R\times R \rightarrow R\times R, dove la funzione \lambda _{v} è espressa dalla 1). Osserviamo innanzitutto  che essendo le \lambda _{v} delle funzioni, possiamo considerare  la  loro composizione. La composizione di funzioni in ogni caso è associativa, lo abbiamo visto nel primo articolo sui gruppi.

Verifichiamo adesso che le  trasformazioni di Lorentz formano un gruppo. Dobbiamo dimostrare che l'operazione composizione è interna, ovvero   °: L x L --->L  , (\lambda _{w},\lambda _{v})\rightarrow \lambda _{u};  la funzione composta, che per ora indichiamo con f=\lambda _{w}\circ \lambda _{v} sarà una funzione f: R x R-->R x R  ; non sappiamo ancora se si tratti di una trasformazione di Lorentz, dobbiamo dimostrarlo.

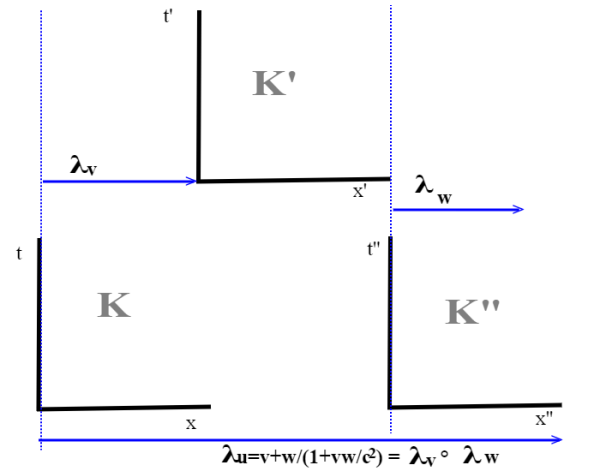
lorentz

abbiamo tre sistemi inerziali, K,K',K''; K' si muove rispetto a K con velocità v, K'' si muove rispetto a K'con velocità w; per calcolare le coordinate di un punto(evento) in K'' in funzione di quelle in K possiamo operare in due modi;

il primo è quello  di calcolare prima la trasformazione di Lorentz da K a K':

\left\{\begin{matrix} x'=\gamma (v)(x-vt))\\ t'=\gamma (v)(t-\frac{v}{c^{2}}x) \end{matrix}\right.

poi riapplicare la trasformazione da K' a K'',

\left\{\begin{matrix} x''=\gamma (w)(x'-wt'))\\ t''=\gamma (w)(t'-\frac{w}{c^{2}}x') \end{matrix}\right.

per esprimere la funzione composta dobbiamo legare (x'',t'') a (x,t), per cui nella seconda dobbiamo sostituire a x',t' le espressioni in funzione di x,t:

\left\{\begin{matrix} x''=\gamma (w)[\gamma(v)(x-vt) -w\gamma(v)(t-\frac{v}{c^{2}}) ]\\ t''=\gamma (w)(\gamma (v))[t-\frac{v}{c^{2}})-\frac{w}{c^{2}}(x-vt)] \end{matrix}\right.

Per quanto complessa, otteniamo una associazione fra f: (x,t)--->(x'',t'').

L'altro modo, è quello di  applicare direttamente una trasformazione di Lorentz fra Ke K'',(sistemi inerziali in moto relativo con velocità u)che chiamiamo

\lambda _{u} : (x,t)--->(x'',t''); chiaramente le due funzioni devono dare gli stessi valori su ogni coppia(x,t)  ,  quindi f=\lambda _{u}; quindi f ha la forma di una trasformazione di Lorentz.

Quale sia la velocità u lo scopriamo subito: conosciamo già la  legge di composizione di due velocità v,w  che è u=\frac{v+w}{1+\frac{vw}{c^{2}}}; ( è stata dimostrata da Vincenzo QUI). Quindi:

\lambda _{v}\circ \lambda _{w}=\lambda _{u}=\lambda _{\frac{v+w}{1+\frac{vw}{c^{2}}}}.

Qual'è l'elemento neutro? è la trasformazione con velocità relativa uguale a zero,ossia \lambda _{0}(i due sistemi sono in quiete).L'inversa? la trasformazione con w=-v. Lo possiamo capire subito così:

\lambda _{v}\circ \lambda _{-v}=\lambda _{u}=\lambda _{\frac{v+-v}{1-\frac{v^{2}}{c^{2}}}}=\lambda _{0} oppure pensando al fatto che se K' si allontana da K con velocità v mentre K'' si avvicina a K' con velocità v allora K,K'' sono in quiete relativa.

Quindi abbiamo verificato tutte le condizioni della definizione di gruppo.

 

Articoli correlati

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.