Categorie: Relatività
Tags: contrazione lunghezze evento quiz relatività ristretta relatività speciale trasformazioni di Lorentz
Scritto da: Vincenzo Zappalà
Commenti:13
QUIZ: Mancato… No, colpito! Impossibile… Un paradosso relativistico? ****
Un bel problemino relativistico (RR) che sembra portare a un paradosso. Un’attenta analisi dei fatti, però, fa rientrare tutto nelle regole… Einstein , per questa volta, si salva. Io lo giudico abbastanza difficile (rispetto a quello della volta scorsa). A voi smentirmi, come fate di solito!
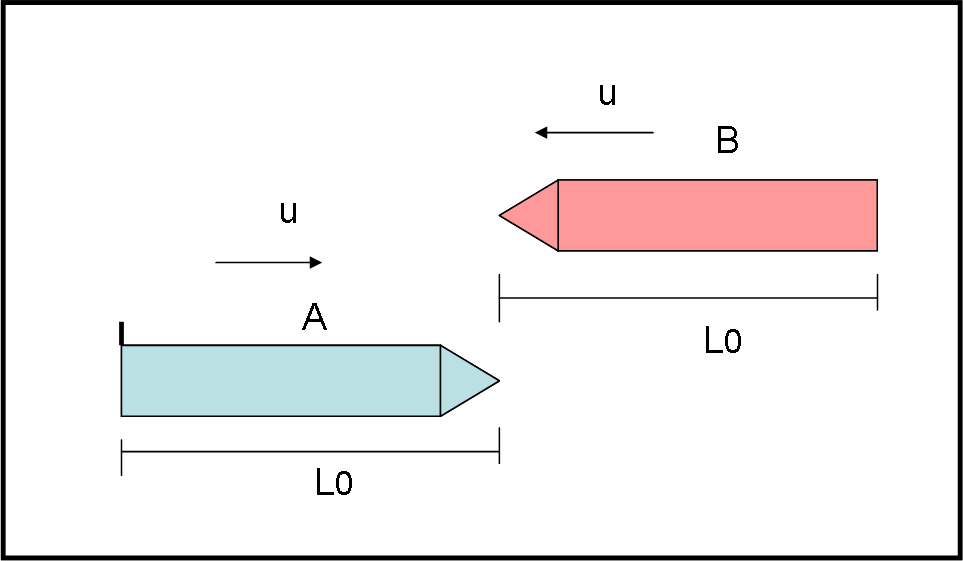
Consideriamo, nuovamente, le nostre due astronavi A e B di lunghezza uguale (Lo). Esse viaggiano una contro l’altra lungo l’asse x, separate da una piccola differenza in y, in modo da non scontrarsi. Ciascuna vede l’altra avvicinarsi con una velocità u (Fig. 1).
Se ci poniamo su A, quando la coda di B tocca la punta di A, un missile viene sparato dalla coda di A verso B (Fig. 2a). Ovviamente il missile andrà a vuoto, a causa della contrazione della lunghezza di B, visto da A.
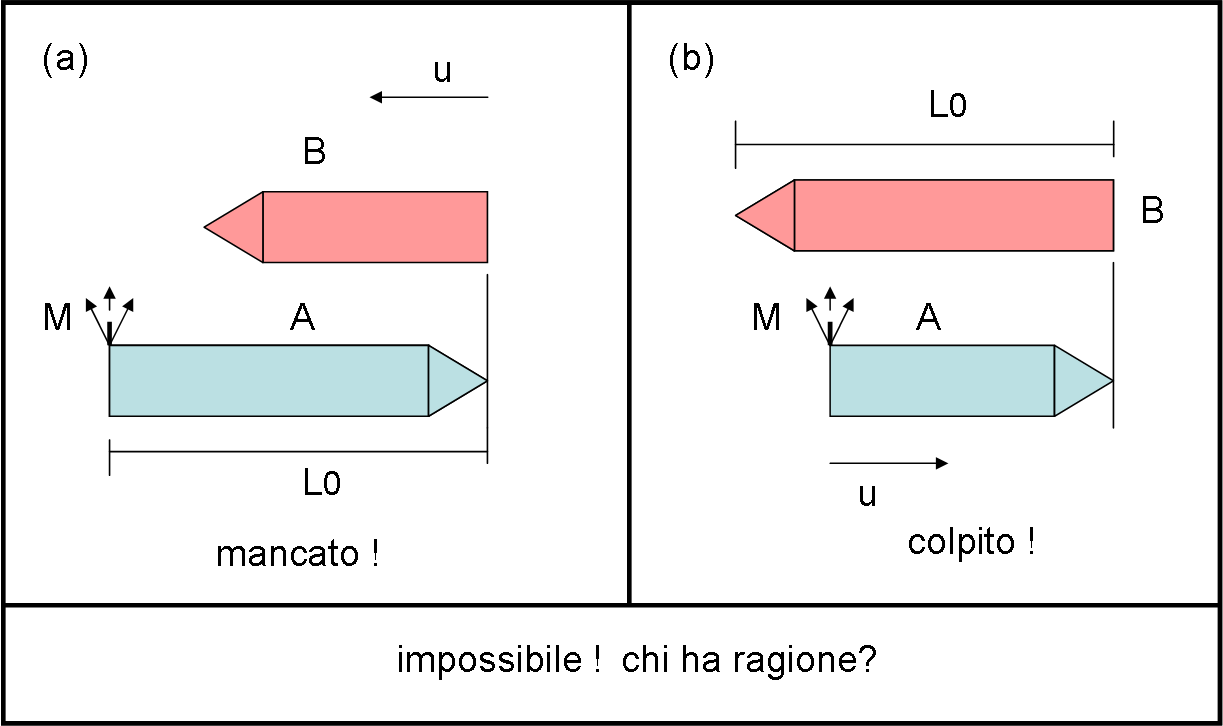
Tuttavia, se ci poniamo su B, la stessa situazione porterà a un colpo vincente del missile di A (Fig. 2b). Attenzione: poniamo uguale a zero il tempo che il missile compie per andare da A a B.
Assurdo! Siamo in relatività ristretta ed entrambi i sistemi devono vedere lo stesso fenomeno, ossia anche B deve concludere che il missile non può colpirlo o viceversa. Chi ha ragione? E perché?
Consiglio di svolgere il problema identificando una serie di eventi E(xA,tA) nel sistema di A e, poi, utilizzare le trasformazioni di Lorentz per ottenere gli stessi eventi nel secondo sistema E(xB,tB)
Il mistero si risolve con dei confronti e con un po’ di ragionamento…
In un secondo tempo (ma non subito, per favore), si potrebbe anche rappresentare graficamente con Minkowski… Ma, prima, esercitiamoci con gli eventi e le loro trasformazioni.






13 commenti
Ti diverti, eh?
ho risolto il problema, non senza fatica, ma sono ancora messo male, ho solo il telefonino, e non riesco a scrivere formule o fare disegni. Lo farò una volta tornato a casa!
per ora dico solo che nessuno si fa male ...e non c' è paradosso!
si vede bene dal diagramma di Minkowski...!
Spero che altri risolvano presto!
saluti
non vedo l'ora, Pippo... per due motivi: dirti bravo e saperti in forma!!!!
Salve Pippo, ti auguro anche io una veloce guarigione (in questo caso una violazione del limite di c ci può stare )
)
In merito al quiz, a ben guardarlo a me somiglia molto al paradosso dello sciatore velocista relativistico (cade o non cade nella buca lunga quanto i suoi sci ?...). E' vero che qui si muove sia l'astronave A che l'astronave B. Però, mi impedisce qualcosa di considerare A ferma e B in moto verso A con velocità u ?
Chiaramente se consideriamo A fermo il missile non colpisce B , ovvero la proiezione degli estremi di A contiene B che da fermo ha lunghezza uguale ad A, ma in movimento viene visto da A come di lunghezza ridotta. Il viceversa non sembra vero; se da B considerato fermo guardo A ; se uno degli estremi coincide, essendo A ridotto la coda sembra cadere internamente a B (è così il missile lanciato con velocità infinita). se considero due eventi simultanei per A (lancio missile e allineamento testa di A con coda di B ) non lo sono per B; ma la lunghezza di B è data da due eventi simultanei per B; se prendiamo come istante di azzeramento l'allineamento testa A-coda B , applicando le trasformazioni di Lorentz trovo che il missile è stato lanciato prima da A, quando la coda di B era ancora fuori portata
ma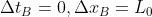 lunghezza propria; sostituendo :
lunghezza propria; sostituendo :
Dobbiamo vedere dove si trovava la coda di A in tale istante; in questo tempo ha percorso uno spazio pari aL_{0}\frac{v^{2}}{c^{2}}) ; per ottenere la posizione totale bisogna sommare questa (in valore assoluto) con la lunghezza L di A vista sempre da B,
; per ottenere la posizione totale bisogna sommare questa (in valore assoluto) con la lunghezza L di A vista sempre da B,
,L_{0}\frac{v^{2}}{c^{2}}+\frac{L_{0}}{\gamma&space;(v)}=L_{0}(\gamma&space;(v)\frac{v^{2}}{c^{2}}+\frac{1}{\gamma&space;(v)}))
ho fatto dei conti, sostituendo a gamma la sua espressione in funzione di c e v; questa quantità risulta maggiore i Lo
aspetterei il ritorno in forma di Pippo, anche se posso anticipare che la sequenza temporale degli eventi in un sistema può essere diversa in un altro... provate pure a usare Minkowski, se volete...
Piccolo suggerimento, purtroppo solo a parole, visto che sono a letto e non posso fare disegni, ma siete comunque bravi!
È vero che si muovono entrambi , ma rispetto a chi ? Non ci interessa ! Allora nulla vieta di assumere B "in quiete" (notate le " ) e A in moto relativo , supp. verso destra, rispetto a B. Fate un diagramma di Minkowski per B: gli estremi percorrono due linee di universo parallele all'asse t verticale, la loro distanza è la longhezza propria L0 della nave B. La striscia verticale di piano compresa è la "striscia " o "tubo " di universo di tutta la nave.
Adesso disegnate la striscia di universo della nave A, che sarà inclinata verso destra di arctg v rispetto alla verticale.
Le due striscie di universo si intersecano, bisogna capire che cosa rappresentano i punti di intersezione delle linee terminali di B e di A. Poi bisogna individuare la lunghezza propria L0 di A e la sua lunghezza contratta: chiaramente la propria è parallela a x' , asse spaziale di A , la contratta è parallela invece a x , asse spaziale di B .
E poi bisogna ragionare: quando la punta di A è nella coda di B , parte il missile trasversale dalla coda di A , ma dove si trova questo " evento" ?
È fuori o dentro la striscia di universo di B?
Eccetera....disegnando il diagramma di Minkowski nel rifermento di A , le cose non devono cambiare !Gli eventi sono sempre gli stessi, visti da due OI diversi!
Pippo, sei stato più che preciso ed è per questo che sono deciso a mandare avanti la proposta appena pubblicata. Spero che tu sarai dei NOSTRI! Pensa, però, a guarire meglio... sei troppo prezioso...
non avevo parlato di diagrammi di Minkowski perchè era stato richiesto esplicitamente di non usarli, e di usare le trasformazioni di Lorentz; è chiaro che si "vede" meglio anche il mio tentativo di spiegazione.Cercherò di completare al più presto.
Vorrei provare anche io a risolvere il quiz… ma non sono sicurissimo che sia tutto corretto.
Premetto che possiamo considerare ciascuna astronave ferma nel suo sistema di riferimento, e considerare sempre e solo l’altra astronave muoversi a velocità v.
Nel caso specifico considero l’astronave A fissa, e l’astronave B’ in moto.
Premetto che ciò che avviene in un sistema deve essere visto allo stesso modo dall’altro sistema.
Considero le astronavi A e B’ entrambe lunghe 1 nel proprio sistema.
La velocità relativa è pari a v=0.6c
Considero che quando la punta di A coincide con la coda di B’ si ha:
Xpunta_a = X’coda_b’ = 0 e i relativi orologi posti in quei punti segnare Tpunta_a = T’coda_b’ = 0.
Se considero un altro orologio posto sulla coda di A sincronizzato con quello della punta, quando entrambi segnano zero parte il missile dalla coda di A. (Tpunta_a = Tcoda_a = 0)
Analizzando dal sistema fisso il missile non colpirà l’astronave B’, perché quest’ultima risulta essere contratta, e quindi essere più corta di A.
Analizzando dal sistema in moto, si dovrebbe dire il contrario, ovvero l’astronave A è più corta di B’ e quindi dovrebbe verificarsi l’impatto.
Così non è, perché la simultaneità degli eventi vista dal sistema in moto è diversa.
Dal punto di vista di B’, quando la punta di A coincide con la coda di B’, l’orologio sulla punta di A segna zero, esattamente come l’orologio sulla coda di B’, ma in quel preciso istante l’orologio posto sulla coda di A visto da B’ non segna più zero, ma un valore maggiore.
Non è in quell’istante che parte il missile nel sistema di riferimento di B’.
Rispetto B’ i due orologi posti rispettivamente sulla punta e sulla coda di A, non sono sincronizzati.
Siccome che lo stesso fenomeno deve essere visto allo stesso modo, ovvero se il missile parte quando l’orologio posto sulla coda di A segna zero, la stessa cosa deve essere vista da B’, ma quando ciò avviene la coda di A vista da B’ si trova in una altra posizione, ovvero fuori dall’ingombro dell’astronave B’.
Anche visto da B’ non avviene nessun impatto.
Provo a fare qualche diagramma di Minkowski.
Spero che si capisca.
Analizzando il secondo grafico dal punto di vista di A, si capisce che, quando la punta di A coincide con la coda di B’, la punta di B’ si trova a X=-0.8 (contrazione delle lunghezze).
Se in quel istante (Tpunta_a = Tcoda_a = 0) parte il missile dalla coda di A, non colpirà mai l’astronave B’, dato che la punta di B’ si trova a X=-0.8, mentre la coda di A si trova a X=-1.
Ma se analizziamo il terzo grafico dal punto di vista di B’, è l’astronave A ad essere contratta (X’=0.8 contro X’=1 della propria lunghezza nel proprio sistema).
Ma è anche vero che in quel istante, quando la coda di A si trova a X’=0.8 il suo orologio segna T=0.6.
Il missile è già partito da un po’di tempo, dato che parte a T=0.
Quindi passiamo all’ultimo grafico, ovvero torniamo un po’ indietro nel tempo, e verifichiamo quanto segue.
Nel sistema di A, quando T=0, la punta di B’ si trova a X=-0.8(come avevo già detto), quindi nessun impatto.
Nel sistema di B’, in quel istante, T’ vale -0.6, e la punta di B’ si trova a X’=1 (notare che è sempre 1 indipendentemente dal suo tempo dato che l’astronave B’ rispetto al suo sistema è ferma e si muove solo nel tempo).
Ma la coda di A si trova a X’=1.25, ovvero maggiore di 1 che è la lunghezza dell’astronave B’ misurata nel suo sistema.
Non può avvenire nessun impatto, anche visto da B’.
Spero di non aver fatto errori grossolani.
Un saluto a tutti.
caro Simone, potresti farmi vedere la contrazione di A vista dal sistema di B, nell'ultima figura?
Mi sa proprio che l’ultimo grafico sia sbagliato … non ho pensato quadrimensionalmente (citazione di un vecchio film…).
… non ho pensato quadrimensionalmente (citazione di un vecchio film…).
Il seguente grafico dovrebbe essere corretto (spero).
Analizzando meglio cosa è simultaneo nel sistema di B’, si ha quanto segue.
Quando nel sistema B’ il tempo vale T’=-0.75, la coda di A segna T=0 (quindi parte il missile), ma visto da B’ si trova a X’=1.25.
Ma dato che la punta di B’ si trova sempre a X’=1 nel suo sistema, non avviene l’impatto.
Invece la punta di A si trova a X’=0.45 e il suo orologio segna T=-0.6.
Si nota che la lunghezza di A visto da B’ è 1.25-0.45=0.8.
Spero di averci preso, dopo una giornata faticosa di lavoro non sono proprio lucido al 100%.
Ciao.
Va bene il nuovo grafico, o è sbagliato?
caro Simone,
direi che ci siamo... comunque oggi stesso esce la soluzione e potrai controllare direttamente...