Categorie: Curiosità
Tags: cinque punte geometria quiz somma angoli stella
Scritto da: Vincenzo Zappalà
Commenti:43
QUIZ: Le stelle sono tante ... **
Sì, le stelle dell'Universo sono tante così come quelle che si possono costruire senza mai staccare la matita dal foglio. Tra le tante, però, ne voglio una in particolare...
La Fig. 1 ci mostra come sia facile disegnare una stella cinque punte, senza mai staccare la matita (spero che sappiate ancora usarla...).
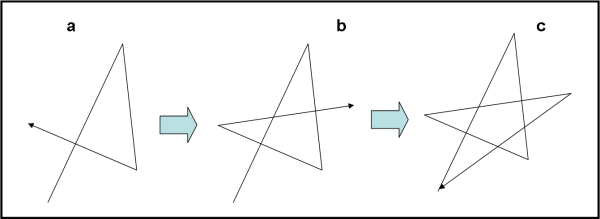
Bene, alla fine otterrete una stella del tutto irregolare come quella di Fig. 2.

Quello che vi chiedo è: "Cosa dovete fare, mentre disegnate la stella, per far sì che la somma degli angoli di tutte e cinque le punte (A + B + C + D + E) sia esattamente uguale a 180°, solamente?"
Sembra difficile... ma si può fare...
QUI trovate tutte le soluzioni che insieme abbiamo trovato





43 commenti
Forse basta ruotare il foglio attorno ad un punto interno di 36 gradi ogni volta che si traccia un lato , mantenendo la direzione e invertendo l'orientamento della linea che si disegna ogni volta...
o no ?
Qualunque sia la stella disegnata, la somma degli angoli delle punte sarà di 180°, purché sia inscritta in una circonferenza.
Infatti sappiamo che, data una corda, l'angolo al centro che insiste su di essa è sempre il doppio di quello alla circonferenza.
Quindi:
Giusto, Valentina, in questo modo gli angoli nelle "punte" possono anche essere tutti diversi ma la loro somma sarà sempre di 180°. Mi domando però perché nella domanda ci sia questa frase: "mentre disegnate la stella" .
Il cerchio circoscritto deve esser disegnato "prima" e non "mentre"...
Ciao e brava!
Ciao Maurizio e benvenuto!
Mi sembra di capire che tu sia appena arrivato, quindi non hai ancora avuto il tempo di renderti conto che Zappi è un grande matematico e scienziato, ma non un "letterato" e a volte va interpretato... ma possiamo perdonargli questi piccoli errorini formali
cara la mia piccola letterata ( ), da quanto ho capito la tua risposta è:
), da quanto ho capito la tua risposta è:
"Qualunque sia la stella disegnata, la somma degli angoli delle punte sarà di 180°, purché sia inscritta in una circonferenza".
Ebbene, la risposta E' SBAGLIATA!
Caro Maurizio, non ti fare suggestionare da queste maghe da quattro soldi... Tu segui la tua strada e non ti curar di loro...
Ma sei proprio tremendo...
Ci penserò, ma ora devo scappare a scuola! Ciao ciao!
cara Vale,
tu sei troppo giovane, ma c'era una canzone che diceva: "Con tutte le ragazze sono tremendo!...." di Rocky Roberts...

[caption id="" align="alignnone" width="300"] Ecco, ho pensato a questa soluzione.... potete scaricare l'immagine a questo link (in verità non sono riuscito ad incorporarla al testo, scusate...)[/caption]
Ecco, ho pensato a questa soluzione.... potete scaricare l'immagine a questo link (in verità non sono riuscito ad incorporarla al testo, scusate...)[/caption]
http://www.bernardiweb.it/santeustorgio/stella.jpg
Traccio il segmento AB - ruoto di un angolo qualsiasi ( meno di 90°) il foglio con centro in B - ora traccio BC (vado verso sinistra) - ruoto il foglio con centro C di un altro angolo qualsiasi ( in modo che l'angolo complessivo sia sempre meno di 90°) - traccio CD (verso sinistra) - ruoto il foglio con centro in D in modo che l'angolo totale sia proprio di 90°. - traccio DA (sarebbe meglio dire DA') verso destra.
Questo segmento DA' è parallelo a AB quindi la stella non si "chiude", però se collego D con A riesco a chiuderla e la somma degli angoli in D e in A è di 90°.
In totale la somma dei 5 angoli è di 180° QED (direbbe Feynman)
Veramente di queste chiusure ce ne sono infinite, perché qualsiasi punto tra X e Y (vedi ultima immagine) è valido.
Aspetto gli insulti e le risate...
Maurizio
caro Mauritius...
sicuramente certe costruzioni sono di uso comune nel quarto Universo a destra, dopo il bivio con quello piatto... ma da noi se ne può fare a meno... (il Circolo capirà presto questo discorso...)
Insomma, cerchiamo di schematizzare cosa fare con questo cavolo di matita in mano!!!
Sto scherzando, ovviamente...

Guarda... è tutto molto più semplice...
E, poi, dovresti sapere che io sono un po' ... bastardino!!!!!
Gàa, in effetti anche il Signor Spock mi ha detto che gli sembrava un po' incasinata come costruzione...
Riproviamo...
Una punta della stella e formata da un triangolo. Alla base di esso c'è un lato di un pentagono.
Se "apro" la catena dei cinque triangoli e allineo tutte le loro basi posso ben dire che gli angoli dei 5 triangoli danno in totale 5*180 = 900°
Ora richiudo la collana dei triangoli.
Il perimetro disegna un grazioso poligono in cui la somma di tutti gli angoli interni è 2*360 = 720°
Questi 720° altro non sono che la somma di tutti gli angoli alla base dei triangoli che formano le punte.
Adesso facciamo la sottrazione 900° - 720° = 180° indipendentemente dalla forma dei triangoli....
Questo vuol dire tutte le stelle che disegno hanno la stessa proprietà: sommando gli angoli in punta ottengo 180°
La risposta è quindi la seguente....Mentre disegno la stella (con una mano), posso fare quello che preferisco.
Ad esempio con l'altra mano posso suonare il piano, intanto canto una canzone, magari con una cannuccia mi bevo un succo di frutta alieno, insomma, mentre disegno la stella faccio quello che mi pare, tanto sono sempre 180°
Spero che così vada bene....
Ciao a tutti
Maurizio
Devo correggere una frase chiave del discorso, scusate.
La somma degli angoli interni del poligono è 360 (non 2*360), però la devo contare due volte perché in ciascun triangolo nel punto di congiunzione con il precedente mi ritorvo lo stesso angolo a sinistra e a destra (2 volte).
Appena posso faccio il disegno così è più chiaro cosa intendo dire...
Provo a dire la mia.
Secondo me la soluzione e' che la somma degli angoli delle punte e' sempre 180 gradi.
Per dimostrarlo ho fatto sto ragionamento.
Prendiamo la stella e osserviamo il pentagono irregolare interno ad essa.
La somma dei suoi angoli interni del pentagono e' sempre di 540 gradi.
Ora prendiamo i 5 triangoli che si formano prendendo ognuno degli angoli del pentagono:
Ognuno di essi comprende due punte e un angolo del pentagono. Ogni triangolo ha una somma di angoli di 180 gradi. La somma di tutti e 5 i triangoli e' 900.
Se togliamo da 900 540, cioe' la somma degli angoli appartenenti al pentagono abbiamo 360, e otteniamo la somma degli angoli delle punte. Ma se consideriamo che la stessa punta appare due volte nei 5 triangoli, allora basta dividere per due: 180
Scusate ancora, ma la figura l'ho già fatta... e non è bellissima!
Sto facendo il trasloco e non ricordo più in che scatolone ho messo il cervello.
Adesso non dico più niente, finché non l'ho rimesso al suo posto.
Maurizio
Scusate, rimetto le immagini (mi rendo conto ora che quelle sopra sono quasi incomprensibili)
La prima e' la stella con evidenziato pentagono interno, e sotto i 5 triangoli costruiti sui suoi angoli.
scusa Mauritius,
mi spiegheresti meglio qual'è il "grazioso" poligono?
Ecco la mia stella di Negroni...
Qualunque stella si disegni, la somma degli angoli delle 5 punte è sempre pari a 180 gradi. Ho volutamente disegnato una stella irregolare. La proprietà geometrica che ho preso in considerazione è quella secondo cui la somma degli angoli interni di un poligono di n lati è pari a 180 x (n-2). Questa vale sia per il pentagono centrale del disegno, sia per i 5 triangoli di vertici A, B, C, D ed E....
caro Mauritius,
penso di aver capito cosa intendi dire ed è la stessa cosa a cui è arrivato Paolo..
Comunque sia, il risultato è giusto (la somma è sempre 180°).
Io ho usato un alto metodo che "mi sembra" più politicamente corretto... lavorando solo su un triangolo, senza scomodare gli altri...
Comunque, ottimo ragazzi e , posso dirlo?, Mauritius mi sembra un ottimo acquisto, vero Paolo? Uno che sta facendo trasloco e che ha tempo per il nostriocircolo deve essere un po' "speciale" come tutti noi!!!
Vediamo se ci arriva anche Valentina...
bravo anche Arturo... ma si può sveltire un po' (almeno io la penso così...)... (anche perché è quella che pensato io
Sì...! bravo Paolo e bravo Arturo ! stavo scrivendo una cosa che sembra la fotocopia del suo quaderno.
A questo punto non serve più. Comunque il grazioso poligono è il corpo pentagonale della stella che sostiene i cinque tentacoli triangoliformi.
Penso che ci siano buone possibilità di snellire il ragionamento riducendolo all'essenziale.
Vedremo.
Ciao a tutti...
Mentre pensavo a come sveltire il procedimento, mi è venuta un'altra pensata , tutta geometrica, basata sul riporto in una delle 5 punte, degli angoli delle altre 4, mediante rette perallele... E il procedimento funziona, alla fine ci si ritrova un angolo piatto come somma degli angoli delle 5 punte.
Quanto sopra per dire che non ho invece ancora scoperto come limitare il procedimento di prima ad uno solo dei 5 triangoli e ora devo scappare al lavoro (sigh.. o per fortuna, dipende dai punti di vista). Pensaci tu Prof
magnifico Arturo... è quella che mi piace più.... ancor meglio della mia!!!!
Forza, trovatene altre, che poi le mettiamo tutte assieme nell'articolo risolutivo!
La collaborazione continua

Bravo anche a te Maurizio.
Anch'io Arturo sto ancora pensando come dimostrare la cosa in modo piu' politically correct... ma per ora sono lontano.
caro Paolo,
prova pure, ma quella di Arturo è nettamente la migliore, la più elegante e senza alcuna formula... Mi inchino...
Tanto di cappello!!!!
Alla fine è venuta fuori questa sequenza di figure esplicativa del procedimento geometrico.
Partiamo da una delle 5 punte. Avendole chiamate con A, B, C, D, E, parto per esempio dalla punta C.
L'angolo in C è già lì. Vado ora a riportare nel vertice C gli altri 4 angoli. Cominciamo , per esempio, con l'angolo in B. Mando da C la parallela al segmento BA:
Si vede subito che gli angoli evidenziati in rosso sono tra loro congruenti perché alterni interni di rette parallele tagliate dal segmento BC.
Ora riporto in C l'angolo in D. Mando da C a parallela al segmento DE.
Di nuovo, si vede subito che gli angoli evidenziati in azzurro sono tra loro congruenti perché alterni interni di rette parallele tagliate dal segmento DC.
Ora riporto in C l'angolo in A. Mando da C le rette parallele ai segmenti AB ed AE.
I due angoli evidenziati in verde sono tra loro congruenti perché compresi tra rette rispettivamente parallele. In pratica è come se traslassimo l'angolo in A fino a far coincidere il vertice A con il vertice C.
Infine, riporto in C l'angolo in E:
In questo caso, l'angolo in E è congruente all'angolo evidenziato con i tre archetti viola , per lo stesso motivo visto sopra (traslazione di angolo). Inoltre l'angolo evidenziato con i tre archetti viola è congruente all'angolo in C evidenziato in viola perché angoli opposti al vertice. Quindi, per la proprietà transitiva della congruenza, i due angoli evidenziati in viola, quello in E e quello in C, sono tra loro congruenti.
Cosa ho ottenuto riportando tutti gli angoli nel vertice C ? Un angolo piatto, e che sia piatto me lo assicura il fatto che il primo lato del primo angolo e il secondo lato dell'ultimo angolo sono allineati (gli angoli in D e in E hanno il lato DE in comune).
E questo per qualsiasi configurazione della stella.
Buonasera Circolo !
Proviamo in quest'altro modo a_scientifico
Disegno un cerchio e ci inscrivo un pentagono regolare (lasciatemi fare). Guardandolo osserviamo che ogni lato si piega rispetto al precedente di 360°/5 in modo da "chiudere il giro".
Ora disegno il prolungamento dei lati del pentagono in modo che si formi la figura del pentalatero stellato, insomma, la stella a cinque punte che nel nostro disegno sarà regolare.
Ogni punta è un triangolo in cui i lati alla base valgono 360/5, lo abbiamo già detto. Ne deriva che l'angolo nel vertice vale esattamente:
180° - 2*(360°/5) che , con facili passaggi, diventa 180°/5 . Avendo in tutto 5 punte la somma dei loro angoli sarà 180°.
Tutta questa regolarità e simmetria l'abbiamo disegnata sul piano.
Ora abbandoniamo Flatlandia e costruiamo un bel prisma retto a base "pentalatero stellato regolare" e saliamoci sopra salutando i flatlandesi.
Prendiamo al volo un punto che passa di lì e facciamo sbocciare da esso una "stella di piani" (non c'entra con la nostra stella di Negroni, è solo l'insieme di tutti i piani possibili che hanno in comune solo quel punto e che sono in numero infinito, inclinati in ogni modo.
Ciascun piano taglia il prisma e, affettandolo, crea una figura deformata della stella a cinque punte. Ciascun angolo non sarà in generale uguale a prima, però...la somma degli angoli interni dei poligoni si conserva, ossia un triangolo della stella avrà una forma diversa ma la somma dei suoi angoli sarà sempre di 180°. Ci mancherebbe altro! Anche per il pentagono vale la stessa cosa, la somma degli angoli interni , che vale 540°, resta invariata.
Quindi il ragionamento fatto per trovare l'angolo di una punta continua a valere, nel suo insieme. Lo so, potrebbe sembrare una idiozia dire questa cosa così, senza darne una dimostrazione. Però preferisco chiamarla "congettura", è più carino. Magari quando ritrovo lo scatolone in cui ho imballato il cervello, cerco di dare una bella dimostrazione.
Se accettiamo questa congettura possiamo fare anche un discorso più generale...
Ad esempio se prendo un esagono "irregolare" e gli costruisco la sua bella stella addosso, sommando gli angoli delle punte cosa troverò?
Scendiamo un momento a Flatlandia e ragioniamo sull'esagono regolare.
Ogni lato si piega di 360°/6 in modo da chiudere il giro...Considero la stella formata dal prolungamento dei lati e posso affermare che in ciascun triangolo-punta i lati alla base valgono 360/6. Ne deriva che l'angolo nel vertice vale 180° - 2*(360°/6) che , con facili passaggi, corrisponde a 180°/3 e, facile, avendo 6 punte avrò in totale 360°. ma lasciatemelo scrivere così...2*180°
Curioso, aggiungendo una punta alla stella abbiamo aggiunto 180° all'angolo totale.
E se ora torno sulla torre a base stella a sei punte e ne faccio l'affettato con i piani "trasformanti" , cosa succede? Vedi considerazioni del caso precedente...
Ma sarà una fortuita coincidenza che aggiungendo una punta ho incrementato l'angolo-somma proprio di 180°?
Proviamo con 7 lati...
Ogni lato si piega di 360°/7 in modo da chiudere il giro...Considero la stella formata dal prolungamento dei lati e posso affermare che in ciascun triangolo-punta i lati alla base valgono 360/7. Ne deriva che l'angolo nel vertice vale 180° - 2*(360°/7) che , con facili passaggi, corrisponde a 180° *3/7 e, facile, avendo 7 punte avrò in totale 3 *180°
La cosa si ripete, e si ripeterà, perché il ragionamento generale dice che
Angolo-somma = N* (180° -2*(360°/N)), che con facili passaggi diventa 180*(N-4) ove, N è il numero di punte.
Quindi pentalatero stellato N=5 Angolo-somma = 180° , perché (5-4)*180° = 180°
esalatero-stellato N=6 360° (6-4)*180° = 2*180°
ettalatero-stellato N=7 540° (7-4)*180° = 3*180°
E così via, sia a Flatlandia che fuori, con figure comunque "deformate" dalle infinite sezioni operate dai piani.
Ultima domanda...visto che andando oltre il pentagono, aumentando il numero dei lati, la cosa funziona in questo modo, funzionerà anche andando indietro?
Già, vediamo...prendiamo il quadrato. Come possiamo costruire il quadrilatero-stellato?
Se prolungo i lati del quadrato ottengo quattro rette parallele a due a due. dove si incontrano le parallele? Difficile a dirsi, ma una cosa, forse, possiamo dirla sull'angolo che è compreso di esse: vale zero (spero sia giusto). Se è così allora 4 volte zero fa zero e questo è il valore dell' angolo-somma.
Cosa ci dice la formula di prima se poniamo N=4? Angolo-somma= (N-4)*180 = (4-4)*180 = 0, Benissimo!
Saliamo sul nostro ascensore terzodimensionale e facciamo esplodere la stella di piani....
Mhhh, quanti rombi, deltoidi, rettangoli, fors'anco trapezi, un solo quadrato, che meraviglia!, già però adesso ho delle stelle molto strane, da una parte le punte si formano ma dalla parte opposta le rette divergono... Ma se la "congettura" vale anche in questo caso, allora devo immaginare che ci siano angoli negativi (dove le punte non si uniscono perché le rette divergono) tali da compensare gli angoli positivi delle punte "normali".
Insomma, non vedo altro modo per avere ancora l'angolo-somma uguale a zero.
E allora, cosa succederà con il triangolo...? Cosa ci riserva il trilatero-stellato?
N=3, Angolo-somma = (3-4)*180° = -1 * 180° = -180° Noooo!
Eppure, vediamo, diegnando per terra (su Flatlandia) il nostro bel triangolo regolare (equilatero). Prolungandone i tre lati, bravo... ma non vedi che li puoi prolungare solo in un senso perché nell'altro sono già fusi nel vertice?
Ecco...diciamo che ogni "punta" (degenere) della "stella" ha una specie di "antiangolo" che vale -60°. Siccome le "punte" sono 3...il totale fa proprio -180. Anche dalla torre a base triangolare.
Adesso devo lasciarvi perché mi hanno già messo la camicia di forza e l'ambulanza è giù che aspetta con il motore acceso.
Grazie per lo spazio-tempo che mi avete concesso. Le dimostrazioni a un altra volta, anzi, magari le lascio fare a uno bravo, che è meglio.
Ciao a tutti.
Maurizio
Bravo Arturoooo ! Ineccepibile direi, oltre che elegante e senza un solo numero da calcolare.
La geometria ha un fascino particolare, come la musica, vale mille parole e infinite formule, entra direttamente nel cervello.
Vediamo se funziona anche questa dimostrazione.
Disegno un triangolo scaleno tipo questo:
La somma degli angoli ABC e' 180 gradi.
Ci costruisco sopra la nostra stella, i tre angoli ABC risultano altrettante punte della stella, ma gli angoli delle punte in B e C sono ridotti rispetto agli angoli del precedente triangolo di una quantita di gradi equivalente alla somma degli angoli B1 e C1, come da figura
A questo punto possiamo dire che se la somma di D+E e' identica alla somma di B1 + C1 allora la somma totale degli angoli tornerebbe ad essere 180 gradi. Ma cio' e' gia evidente, perche' gli angoli Z e z1 sono uguali, e se sono uguali la somma degli angoli rimanenti e' necessariamente identica.
Sì che funziona, Paolo...ed è anche molto, molto sintetica.
Ti basta una "dimostrazione" empirica?
Perché le hai rotte..? erano così belle!
Ciao Valentina,
Vedrai che qualcuno dirà che hai preso gli unici due casi particolari favorevoli ...Comunque non preoccuparti, sei in buona compagnia, pensa che più di 400 anni fa, Galileo, non riuscendo a dimostrare il rapporto tra area della cicloide e del cerchio generatore, ritaglio dei pezzi di metallo sagomati nelle due forme e li pesò, arrivando a concludere ciò che sospettava area cicloide= 3 volte area cerchio.
Comunque è una autopsia molto convincente.
Ciao
Maurizio
Grazie Maurizio... ma non sono sicuro di avere compreso la tua "congettura" tridemensionale
Arturo, la dimostrazione grafica e' veramente elegante.
Anche il metodo empirico di Valentina ha il suo effetto, anche perche' con le sue due stelle si fa sempre l'angolo giro, e potrebbe alternare i colori a piacimento senza timore di non chiuderlo.
Grazie per l'idea, Maurizio! Se qualcuno molto pignolo e severo dirà che ho trovato gli unici casi particolari, gli ricorderò la storia di Galileo.
Avrei voluto dimostrarlo in modo matematico, ma dopo aver letto i Malavoglia, avevo solo voglia di divertirmi un po'!
Ciao Paolo, vedo di spiegarmi meglio.
Il calcolo basato sulla figura regolare si sviluppa su tutta la catena di angoli che coinvolgono il poligono, operazione facile e immediata proprio per la sua regolarità. L'idea è che, anche se nella figura deformata i singoli angoli si modificano, l' insieme degli angoli di una figura chiusa mantiene il medesimo valore. Facevo l'esempio dei triangoli i cui angoli sommati danno ancora 180°, quindi i cinque triangoli mi daranno complessivamente, comunque 900° (che caldo!). Facevo anche il caso del pentagono che, pur essendo ora deformato, continua ad avere tutti i suoi 540° all'interno. Insomma, agendo sui totali la deformazione non produce effetti, quindi la conclusione a cui sono arrivato studiando il poligono regolare, adagiato sul piano orizzontale, vale anche per una qualsiasi figura, deformata nel modo che ho indicato.
Forse ho peggiorato la situazione....
Ciao
carissimi... siete stati trascinanti e trascinati da una stella qualsiasi. Grandioso. E abbiamo ance la prova pratica alla "Arturo", ma questa volta fatta dalla nostra Vale che deve riuscire a bilanciare Verga con le stelle...
Una discussione entusiasmante che sarebbe da pubblicate tale e quale. L'idea è quella di cominciare piano piano e poi concludere con la splendida generalizzazione di Maurizio, dando il giusto rilievo alla eleganza di Arturo. L'ultima soluzione di Paolo assomiglia un po' alla mia e troverà posto tra le "così-così".
Lascerei invece perdere il passaggio alle 3d... non vorrei che qualcuno dimostrasse che lo spazio non è curvo, ma fatto a stella!!!!
Posso ardire di chiedervi una dimostrazione scritta per bene e con tutte le figure del caso (soprattutto Maurizio, perché Arturo è stato più che esauriente...) in modo che le possa raccogliere e inserire tutte nella soluzione? Compresa la stella che si apre e si richiude, perché resta un po' ambigua la spiegazione... Mandatemela all'indirizzo privato...
Potrei farcela do solo, ma se mi aiutaste ve ne sarei MOLTO grato...
Controproposta per non darvi ulteriore lavoro (avete già fatto tanto e bene!): provo a scrivere io l'articolo con tutte le vostre soluzioni. Ve le mando e se siete d'accordo mi date il via, OK?
Cari tutti,
mi dispiace per voi (e per il mio caro Enzo che non se n'è accorto ), ma nessuno ha RISPOSTO al quiz. La domanda e:
), ma nessuno ha RISPOSTO al quiz. La domanda e:
"Cosa dovete fare, mentre disegnate la stella, per far sì che la somma degli angoli di tutte e cinque le punte (A + B + C + D + E) sia esattamente uguale a 180°, solamente?"
Quindi la risposta giusta è NIENTE DI PARTICOLARE (o qualcosa di simile)... la dimostrazione è un optional
Ok, ok... non ti arrabbiare, Enzino, mi tiro le orecchie da solo e rientro nei ranghi non importa che mi mandi la stessa autoambulanza che ha portato via Mauritius, tanto io le braccia per infilare la camicia di forza non ce le ho!!
non importa che mi mandi la stessa autoambulanza che ha portato via Mauritius, tanto io le braccia per infilare la camicia di forza non ce le ho!! 
cari amici,
questa discussione rasenta il capolavoro assoluto, tra traslochi, cervelli dimenticati, stelle che pungono, spazi a punta e risposte non date. Il Circolo ringrazia di cuore!!!!! anche perché si è parlato di geometria, matematica (e non solo) in maniera divertente, ma di alto livello... Più di così...


Perdindirindina!!
Se neanche io riesco a farlo arrabbiare con le mie stupidaggini, vuol dire che è davvero al settimo cielo... ops... al millesimo universo parallelo!!
Eh sì, anche perché il piccolo asteroide mi ha commosso, al pari di questo nostro circolo che è andato oltre le più rosee previsioni!!! Viva Scherzy!!!!!!!!!!! (forse anch'io ho perso il cervello....)

Ma noooo... Stai tranquillo, Enzino, ho già chiamato io l'autoambulanza e gli ho dato il tuo indirizzo, fra poco dei signori gentili e sorridenti ti accompagneranno a fare un giro turistico e, se ti comporterai bene, ti lasceranno anche le braccia libere e ti faranno ammirare il panorama!
Aggiornamento traffico e viabilità su strade e autostrade d'Italia.
" Si segnala un gigantesco ingorgo di ambulanze in zona "Infinito teatro del Cosmo" - non è ancora chiara la causa, vi terremo informati con i prossimi notiziari"