Categorie: Fisica Fisica classica
Tags: Lagrangiana Metodo di Lagrange
Scritto da: Fabrizio
Commenti:5
Fabricius e la pietra Lagrangiana - seconda parte
La puntata precedente abbiamo visto che la lagrangiana è data dall'energia cinetica – energia potenziale.
In questa seconda parte inizio a proporvi alcuni esempi con i quali ho cercato di esplorare alcune delle forme che può prendere la lagrangiana a secondo del tipo di coordinate e di riferimento che scegliamo. Questi esempi vorrebbero introdurre gradualmente quello che serve per applicare il metodo di Lagrange alla ricerca dei punti lagrangiani.
Per trovare la lagrangiana provo a seguire questo procedimento:
-
scelgo le coordinate;
-
esprimo l'energia cinetica nelle coordinate scelte;
-
esprimo l'energia potenziale nelle coordinate scelte.
Prima di iniziare vi chiedo la cortesia di farmi sapere tramite i commenti se la lettura di questa parte dell'articolo o delle successive non ha incontrato le vostre attese per qualsiasi ragione (noiosa, poco chiara, troppo difficile, troppi dettagli inutili....). Sapendolo, forse, riesco a modificare qualcosa con l'aiuto dei vostri suggerimenti.
La nostra prima lagrangiana
Partiamo dal caso apparentemente più semplice. Un oggetto di piccole dimensioni tanto da poter essere approssimato ad un punto, spesso viene chiamato "punto materiale". Supponiamolo totalmente isolato, quindi non soggetto a forze e libero di muoversi in qualunque direzione.
Possiamo scegliere le usuali coordinate cartesiane per descrivere il movimento di questo punto. Non essendoci direzioni preferenziali possiamo orientare le coordinate in un modo qualunque.
L'energia cinetica è come sempre che dobbiamo esprimere con le sue componenti lungo le coordinate scelte (vx,vy,vz). Il movimento del nostro punto è libero da vincoli, quindi la sua velocità potrebbe avere qualsiasi direzione. Per questo decomponendola lungo i tre assi che abbiamo scelto si possono ottenere tutte tre le componenti diverse da zero. Le tre componenti sono perpendicolari tra loro e questo ci permette di esprimere v2 applicando per due volte il teorema di Pitagora per trovare le ipotenuse prima del triangolo PRQ e poi del triangolo PQV.
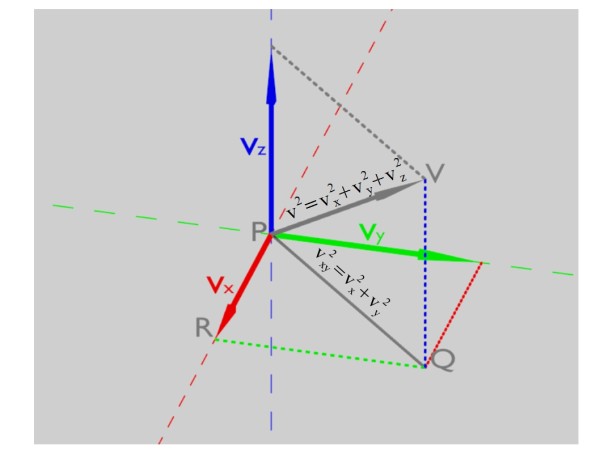
Nel caso di punto materiale isolato la lagrangiana quindi sarà:
Il simbolo con il punto sopra è una notazione che risale a Newton stesso ed indica la derivata temporale (Lui avrebbe detto flussione) della funzione che sta sotto, cioè . Conviene utilizzarla perché rende più leggibili le formule che troveremo più avanti.
Questa è la nostra prima lagrangiana che di fatto non è la più semplice poiché chiama in causa tutte le componenti della velocità.
Il punto materiale libero e la gravitazione
Se il punto materiale libero di questo primo esempio lo collochiamo nei pressi della superficie terrestre occorre considerare anche l'energia potenziale gravitazionale, ma prima dobbiamo definire le nostre coordinate.
Ora c'è un orientamento preferenziale dato dalla direzione verticale della forza di gravità. Le coordinate cartesiane sembrano ancora andare bene, ma conviene allineare un asse con la verticale, diciamo l'asse z.
L'espressione dell'energia cinetica rimane invariata poiché il punto è ancora libero di muoversi in ogni direzione. L'energia potenziale gravitazionale nei pressi della superficie terrestre è:
( abbiamo scelto come livello di riferimento il livello z=0).
Quindi la lagrangiana in questo caso sarà:
A mio parere, questa potrebbe essere la soluzione del piccolo quiz che ho proposto alla fine della prima parte.
In effetti nella formulazione del quiz, dicendo che il corpo veniva lasciato cadere verticalmente, ho dato una indicazione che può avere una interpretazione ambigua. Quel "verticalmente" può essere interpretato come un vincolo nel movimento, cioè il corpo non è libero di muoversi in ogni direzione, ma può solo muoversi lungo la verticale. Con questa interpretazione la lagrangiana sarebbe:
Questa mia imprecisione mi torna utile per introdurre la terza parte di questo articolo dove proporrò alcune lagrangiane di corpi non più totalmente liberi di muoversi in ogni direzione, ma vincolati a seguire certe traiettorie.
Il metodo di Lagrange è nato proprio dallo studio di problemi con corpi vincolati. Vedremo come la lagrangiana semplifica questi problemi e come la scelta delle coordinate aiuta ad ottenere questa semplificazione.
La serie completa degli articoli sulla Lagrangiana la trovate QUI






5 commenti
di bene in meglio, Fabrizio... grazie
Innanzitutto volevo ringraziare Fabrizio per questi articoli...
Ti dirò che questo secondo articolo, per quanto mi riguarda, è stato utilissimo per comprendere quello precedente.
Per testare se l'ho compreso davvero, volevo chiedere, se il punto materiale si trova vicino ad un corpo di grande massa M diverso dalla Terra, considerato che l'accelerazione di gravità è uguale a GM/r², l'espressione Lagrangiana potrebbe diventare così?
£ = ½ m ((dx/dt)² + (dy/dt)² + (dz/dt)²) – mz (GM/r²)
Inoltre se non si conosce la Massa M del corpo, ma questo è rappresentabile come una sfera composta di materiale avente un certa densità costante ρ, che occupa un certo volume, si potrebbe anche sostituire alla massa la densità per il volume di una sfera:
M = volume * densità
Volume sfera = 4π R³/3
M = ρ 4π R³/3
£ = ½ m ((dx/dt)² + (dy/dt)² + (dz/dt)²) – mz (Gρ 4πR³/3r²)
Se il punto materiale si trova in prossimità della superficie della sfera r =R, orientando come prima l'asse z, r non è altro che una distanza misurata sull'asse z e l'equazione dovrebbe diventare:
£ = ½ m ((dx/dt)² + (dy/dt)² + (dz/dt)²) – mz (Gρ 4π r/3)
E' corretto un simile ragionamento?
Paolo
Grazie a te Paolo per il commento.
Il ragionamento che fai mi sembra corretto.
E' importante ricordare per i passi successivi che vedremo prossimamente che i fattori (GM/r²) e (Gρ 4π R/3) in questo ragionamento sono delle costanti.
Quindi non contengono neanche implicitamente nessuna delle tre coordinate del punto.
Perchè tieni a dire "r non è altro che una distanza misurata sull'asse z"?
Il ragionamento mi sembra funzioni anche senza questa affermazione.
Fabrizio
Sicuramente la frase funziona anche senza questa precisazione.... più che altro intendevo dire che l'asse Z è quello orientato verso il centro di massa.... e se non ho inteso male, nella tua figura z = 0 rappresenta il suolo (livello di riferimento, così da poter usare g come valore di accelerazione per indicare l'energia di potenziale).
Paolo
Paolo,
la mia domanda era collegata al fatto che in questo caso r va considerato una costante e non c'è dipendenza tra r e z. Ma dalla tua risposta mi sembra che non intendevi indicare questa dipendenza, quindi tutto ok.
Per quanto riguarda il livello di riferimento credo ci sia un margine maggiore di flessibilità di quello che indichi.
z=0 non credo debba essere necessariamente al livello del suolo. Se accettiamo l'approssimazione di una g costante in tutta l'area che occupa e occuperà il nostro sistema, possiamo posizionare z=0 a qualsiasi altezza almeno nell'ambito di questa area.
E' vero che così otterrei valori diversi di U per la stessa posizione a secondo di come posiziono z=o, ma questo non ha effetti fisici che dipendono solo dalle variazioni di U e non dal suo valore assoluto.
Nella prossima parte dell'articolo sulla lagrangiana c'è proprio un esempio che sfrutta questa possibilità.
Fabrizio