Verso Eulgrange

09/01/17

Verso Eulgrange

Categorie: Fisica Fisica classica Matematica Tags: Scritto da: Fabrizio Commenti:4

L'equazione di Eulero-Lagrange richiede che siano fatte alcune derivate della lagrangiana.

dragone

A prima vista queste derivate hanno un aspetto che potrebbe intimorire, ma dietro l'apparenza non c'è niente di particolarmente difficile rispetto a quelle ben spiegate da Enzo nei suoi articoli.

Occorre solo farci l'abitudine.

 

Per iniziare a familiarizzare con queste derivate, ho pensato di proporvi questo percorso suddiviso in tre tappe che ci avvicina alla equazione di Eulero-Lagrange.  Strada facendo incontreremo uno degli aspetti che mi ha inizialmente confuso e vedrete che l'apparenza inganna.

 

Allora, se vi va, partiamo verso la prima tappa!verso_eulrange_1

percorso

 

 

 

1a-tappa

Appuntatevi le vostre risposte alla domanda di questa tappa prima di passare alla tappa successiva. Per il momento non inseritele nei commenti. Questa è solo la prima tappa, al contrario dei telequiz, sarà l'ultima risposta quella che conta.

Quali sono le derivate delle funzioni elencate sotto?

                         per ciascuna elenco  3 possibilità

\begin{aligned}&\frac{w^2}{2}\;\; \; \; \; &A: 0, \,\;\; \; \; \; \; \; \; &B:w, &C: w\dot w \; \; \; \; \; \; \\ &\cos(\theta )\;\; \; \; \; &A: -\sin(\theta ), \; \,&B:0, &C: -\dot \theta \sin(\theta )\\ &2\sqrt{s\;} &A: \frac{\dot s}{\sqrt{s}} ,\; \; \,&B:0, &C: \frac{1}{\sqrt{s}} \; \; \; \; \end{aligned}

In caso di dubbi c'è sempre la possibilità di consultare gli articoli di Enzo elencati dal 23 al 30 in questo approfondimento, in particolare gli articoli elencati ai punti 26, 27 e 28.  Nell'articolo al punto 27 c'è la derivata di xn, considerate che n non è necessario sia intero, ad esempio può essere anche 1/2.

 

Se hai finito la seconda tappa è qui.

percorso

 

 

 

2a-tappa

In questa seconda tappa iniziamo a ragionare sulle possibili derivate di una lagrangiana.

Prendiamo la lagrangiana del pendolo, che riscrivo in questo modo:

\bg_white \large { { \mathfrak{L}=\frac{1}{2}\, m\, r^2 {\dot {\theta}}^2 - m\, g\, r + m\, g\, r \cos(\theta)}} , dove m g ed r sono costanti.

Ricordo che il simbolo con il punto sopra indica la derivata rispetto al tempo.

Questa è la domanda.

Rispetto a quali variabili si può derivare questa lagrangiana ottenendo un risultato non nullo?

Una è evidente nella formula. Una non si vede nella formula, o meglio, si intravede in un punto, ma è inesorabilmente presente. Un'altra può non sembrare una variabile, ma piace molto a Lagrange.

Forse a prima vista non sembra, ma questa domanda ha molto a che fare con la domanda della prima tappa.

Se hai finito la terza tappa è qui.

percorso

 

 

 

3a-tappa

lookingbackward

In questa terza tappa diamo una occhiata indietro al percorso fatto.

Nella seconda tappa abbiamo esplorato la possibilità di derivare una funzione come la lagrangiana rispetto a diverse variabili.

Dopo l'esperienza della seconda tappa riconsideriamo la domanda della prima tappa.

Quali sono le derivate delle funzioni elencate sotto?

                        Per ciascuna elenco  3 possibilità
\begin{aligned}&\frac{w^2}{2}\;\; \; \; \; &A: 0, \,\;\; \; \; \; \; \; \; &B:w, &C: w\dot w \; \; \; \; \; \; \\ &\cos(\theta )\;\; \; \; \; &A: -\sin(\theta ), \; \,&B:0, &C: -\dot \theta \sin(\theta )\\ &2\sqrt{s\;} &A: \frac{\dot s}{\sqrt{s}} ,\; \; \,&B:0, &C: \frac{1}{\sqrt{s}} \; \; \; \; \end{aligned}

È una domanda completa? Manca qualcosa nella domanda?

Se avete dato una risposta nella prima tappa, quale è o quali sono le domande complete alle quali avete realmente risposto?

La serie completa degli articoli sulla Lagrangiana la trovate QUI

Articoli correlati

4 commenti

  1. maurizio
    09/01/2017 at 18:26

    Ciao Fabrizio,

    riguardo alla prima domanda occorrerebbe specificare se le variabili  w ,  θ  ed s  sono funzioni del tempo, se si intende derivarle rispetto al tempo e se le funzioni non sono "funzioni di funzioni".

    Sotto queste ipotesi le risposte sono rispettivamente B, A, C

    se, viceversa,  w  θ  ed s sono costanti nel tempo, i risultati di una derivazione saranno sempre nulli:  A, B , B

    Nel caso di variabili che siano funzioni di funzioni avremo l'ultima terna di risultati  C, C, A

     

    Sulla seconda domanda penso che le variabili rispetto alle quali si può derivare siano   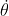\theta , \dot{\theta }  e il tempo t

     

  2. Fabrizio
    10/01/2017 at 09:23

    Ciao Maurizio,
    aspetto a dire la mia per qualche giorno.
    Comunque mi sembra che hai sostanzialmente colto quello che era l'obiettivo del percorso.
    Forse le ipotesi che indichi per ciascuna delle soluzioni possono essere riordinate e sfoltite.
    Grazie per il commento che mi è molto utile per capire come è percepito l'articolo.
    Fabrizio

  3. peppe
    10/01/2017 at 10:03

    caro Fabrizio grazie per i tuoi contributi. dovrò studiare tanto per mettermi al passo con voi, ma vi leggo lo stesso con piacere.

  4. Fabrizio
    10/01/2017 at 15:40

    caro Peppe,
    grazie a te per il commento.
    S fortunatamente, abbiamo tutti da studiare tanto per metterci al passo con quello che vorremmo sapere.
    Spero che questi articoli contribuiscano a farti fare qualche passo nella direzione che desideri.
    Fabrizio

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.