Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Sappiamo già che la parallasse stellare era stata prevista da quel genio assoluto che era Aristarco,  che aveva anche cercato inutilmente di misurarla. Sarebbe stata la prova diretta della teoria eliocentrica. Purtroppo per avere questa “prova” si dovette aspettare il 1727 d.C. per merito dell’inglese James Bradley, ma attraverso un fenomeno del tutto inatteso. Lasciatemi colorire un po’ la “storia”.

Era ormai più di un secolo che  Galileo aveva usato il telescopio per cambiare volto al Cosmo. Tuttavia, la prova diretta della teoria copernicana non era ancora stata ottenuta. Per ottenerla bisognava rifarsi ad Aristarco e “vedere” la rivoluzione della Terra impressa nella variazione apparente della posizione di una stella nel cielo. In altre parole, misurare la sua parallasse.

Nel 1727 Bradley si convinse che la strumentazione era giunta al livello necessario e si dedicò a studiare la variazione della posizione apparente di una stella scelta in modo che gli altri fenomeni come la rifrazione non dessero troppo fastidio. La candidata fu γ Draconis. La osservò durante un anno intero e sembra ancora di vederlo gridare: “Eureka!”. Ce l’aveva fatta, la stella si spostava nel cielo seguendo un’ellisse, proprio quella prevista da Aristarco. La prova decisiva che la Terra rivolveva attorno al Sole. Finalmente…

I guai, però, cominciarono presto: la stella scelta doveva essere veramente vicina, molto di più di quanto si pensasse. Lo spostamento era di 20 secondi d’arco che corrisponderebbero (con le nostre unità di misura) a circa 0.16 anni luce (più o meno). Molto, comunque, ma non poi così tanto. La strumentazione era ormai più che capace di misurare senza errori significativi un angolo di questo tipo. Questa sembrava, perciò, la realtà…

Bradley, però, iniziò a misurare altre stelle in posizioni diverse rispetto all’eclittica e ciò che trovò gli fece rizzare i capelli in testa (sempre che fossero realmente suoi e non solo una parrucca). Tutte le stelle mostravano uno spostamento massimo uguale a 20 secondi d’arco. Le ellissi apparenti si schiacciavano ma il semiasse maggiore restava uguale. Per una stella proprio sull’eclittica l’ellisse diventava un piccolo tratto “rettilineo”, il cui spostamento rispetto al centro, però, era sempre di 20 secondi circa.

La conclusione sembrava ovvia e sconvolgente: le stelle erano proprio fisse e tutte poste alla stessa distanza da noi. Era stata dimostrata la teoria copernicana, ma si doveva accettare una specie di telone sferico (sfera di cristallo) su cui erano incastrate le stelle. Accidenti… qualcosa doveva essere sbagliato.

Bradley, tutto era meno che uno sprovveduto e, inoltre, aveva un’intelligenza fuori dal comune. Iniziò, quindi, a pensare e a … controllare. Sì. qualcosa di strano accadeva veramente. Si formava l’ellisse parallattica è vero (o qualcosa che le assomigliava molto), ma lo spostamento della stella era “sfasata” di 90° rispetto a quella prevista a causa della parallasse. Cerchiamo di comprendere bene questo punto, richiamando cosa si dovrebbe vedere nel caso si misurasse veramente la parallasse stellare.

Mettiamoci nelle condizioni più semplici, ossia consideriamo una stella posta perfettamente nella direzione del polo dell’eclittica, ossia perpendicolare all’orbita terrestre.

Consideriamo, perciò, la Fig. 12

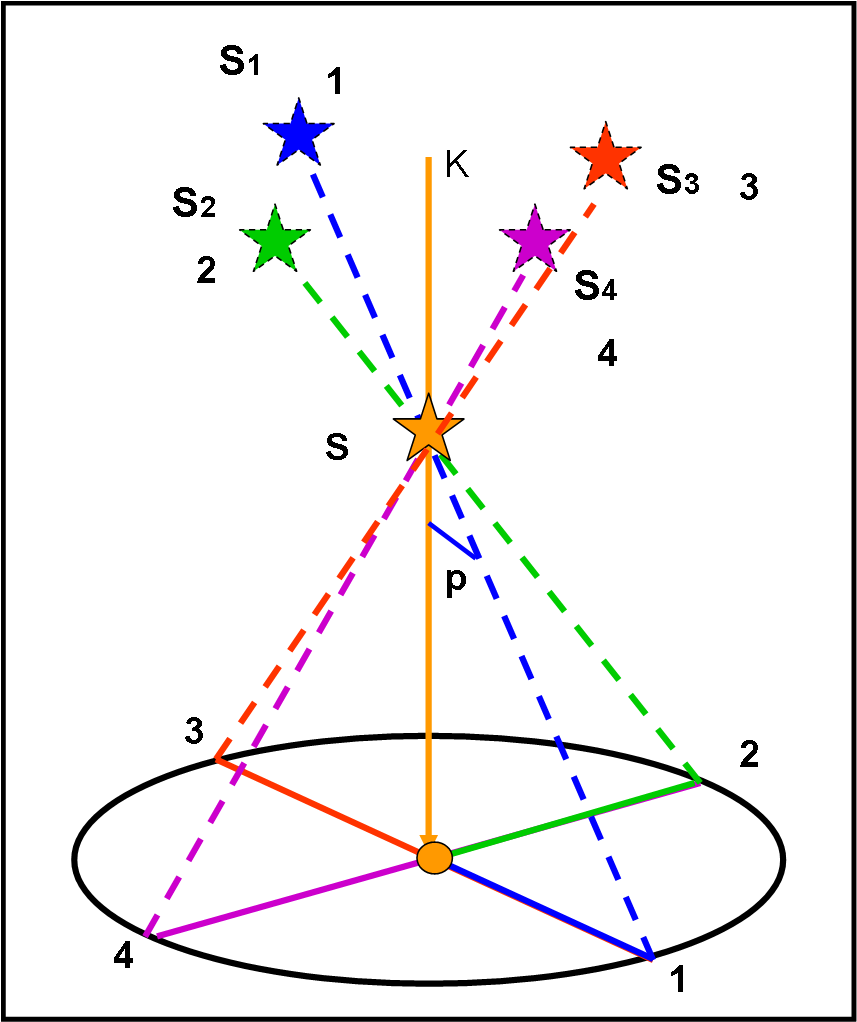
Segniamo 4 posizioni lungo l’orbita terrestre considerata circolare (1, 2, 3 e 4). La posizione vera della stella sia S.

Si tracciano facilmente le direzioni della stella viste dai quattro punti, che differscono tra li loro di circa tre mesi. Nel sistema di riferimento dell’osservatore (che, come al solito si considera fermo), le quattro direzioni danno luogo al cono di Fig. 13.

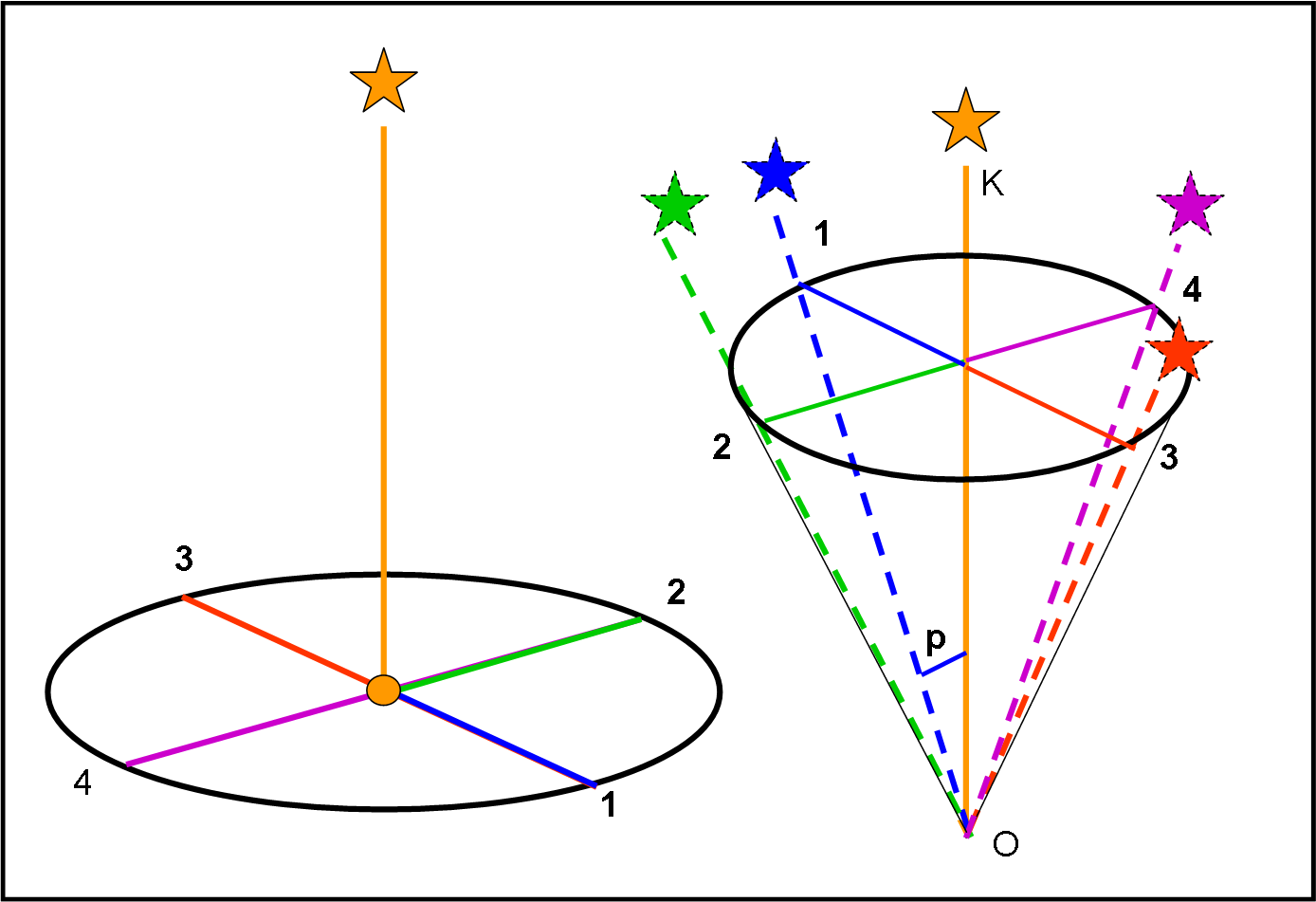
Si vede molto bene come la posizione 1 dia luogo alla direzione di S₁, la posizione 2 alla direzione S₂ e via dicendo. In poche parole, se mi sono spostato verso destra rispetto al Sole seguendo l’orbita terrestre, la direzione apparente della stella si è spostata verso sinistra rispetto al Sole.

L’apertura del cono p è proprio l’angolo di parallasse e dipende fortemente dalla distanza della stella dal Sole. Ovviamente, in questa configurazione (stella perpendicolare al piano dell’eclittica), l’ellisse di parallasse diventa proprio una circonferenza. Per ottenere un’ellisse basterebbe inclinare la direzione della stella S (ad esempio verso la posizione 1). L’asse maggiore rimarrebbe quello che corrisponde alle direzioni 2 e 4, ossia non cambierebbe mai al variare della direzione e a parità di distanza,  mentre l’asse minore sarebbe lungo la direzione da 1 a 3 e quindi si accorcerebbe sempre più. Al limite, per una stella posta proprio sull’eclittica, l’ellisse si ridurrebbe al “segmento” nella direzione da 2 verso 4. In ogni modo, a parità di distanza, il valore del semiasse maggiore, diventato segmento, sarebbe sempre p.

Possiamo vedere l’intera faccenda nella Fig. 14, dove l’orbita terrestre è vista di taglio (direzione da 1 a 3).

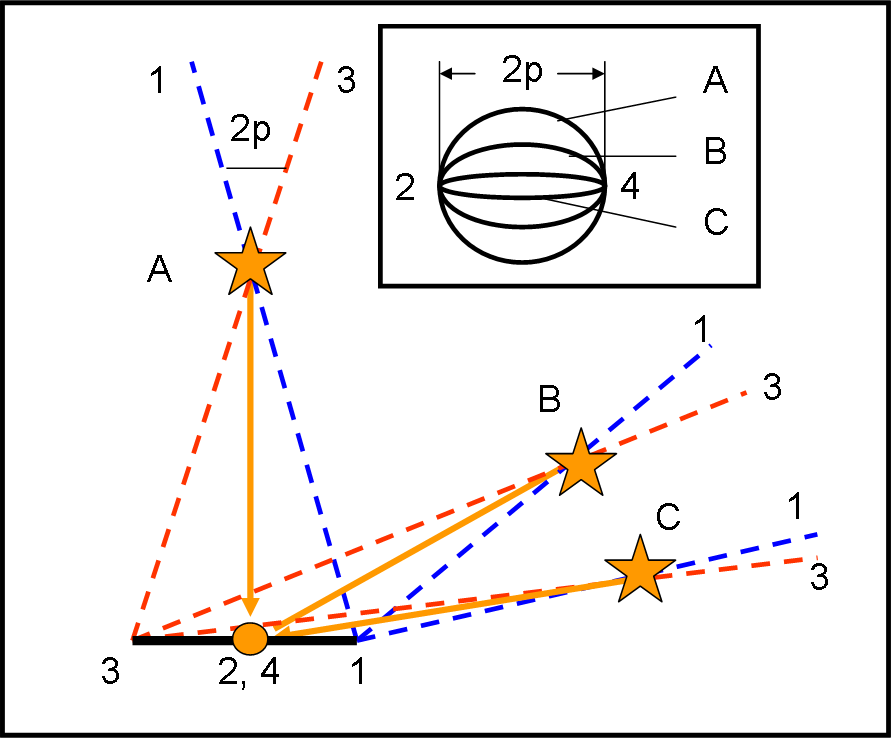
La stella S assume tre posizioni (A, B e C). Nel caso A siamo nel caso precedente e l’ellisse risulta una circonferenza di diametro 2p. Nel caso B, direzione inclinata verso 1, l’ellisse mantiene l’asse maggiore uguale a 2p (due volte l’angolo di parallasse), ma l’asse minore si restringe, per diventare quasi nullo per la posizione C. Il valore del semiasse minore è facilmente ricavabile, ma lo faremo con maggiore precisione riferendoci al quarto sistema di coordinate celesti.

Le cose cambiano di molto se ci occupiamo dell’aberrazione. In questo caso non è necessario fissare una distanza per la stella S. La distanza non conta assolutamente niente e porterebbe a una inutile confusione. Possiamo, perciò, considerare una stella all’infinito in modo che i suoi raggi siano paralleli e tutti perpendicolari al piano dell’eclittica (Fig. 15).

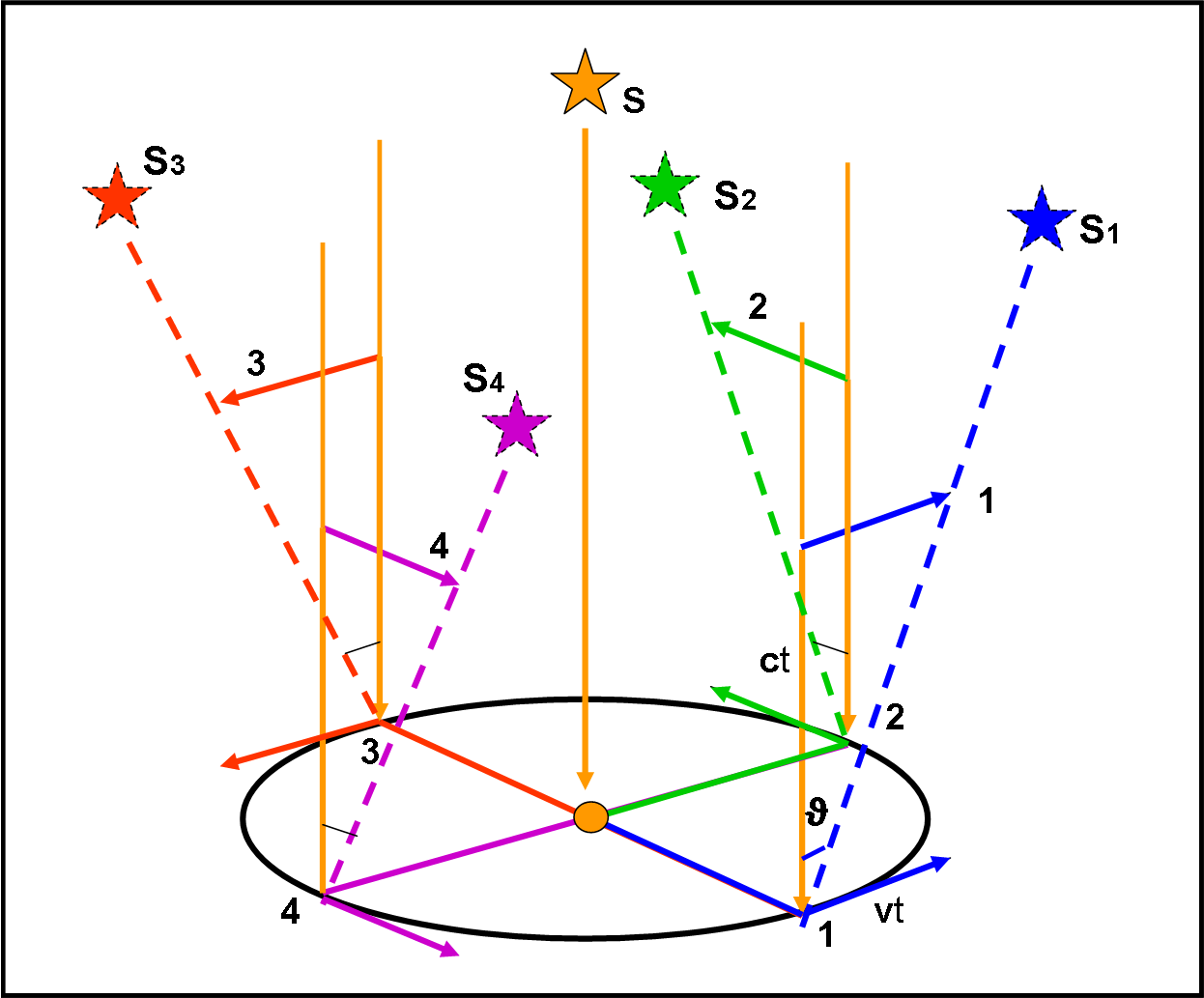
Consideriamo nuovamente le quattro posizioni di prima (1, 2 , 3 e 4). Cosa succede in 1? La stella viene vista più in basso rispetto alla direzione vera, secondo quanto spiegato la volta scorsa. Per  trovare l'angolo di "inclinazione" del telescopio, possiamo considerare il tragitto della luce dal momento in cui tocca l'obiettivo del telescopio fino ad arrivare al fuoco. Esso è dato da ct. Nello stesso tempo t il telescopio si è spostato di vt (dove v è la velocità della Terra).  E’ facile disegnare la linea tratteggiata azzurra che forma un angolo ϑ rispetto alla verticale, proprio l'angolo di cui dobbiamo inclinare il telescopio per vedere la stella. Trovato l'angolo possiamo mandare la linea fino alla sfera celeste, dove si possono leggere solo angoli tra i vari astri.

Stiamo molto attenti a ciò che stiamo per dire: alla posizione 1 corrisponde lo spostamento 1. La stessa cosa capita per le altre tre posizioni. Dopo un anno l’osservatore disegna ciò che ha osservato nel suo sistema di riferimento, come mostra la Fig. 16. Tutte le linee dirette verso la stella apparente, nei vari punti dell'orbita, vengono, ovviamente, disegnate a partire da un unico punto-osservatore O. L'ellisse a sinistra indica il percorso effettuato dall'osservatore lungo l'orbita. L'ellisse a destra è quella che identifica il cono formato dalle corrispondenti direzioni apparenti della stella. Per una posizione 1 a sinistra, corrisponde la direzione 1 a destra. Si vede chiaramente che la posizione del punto sull'orbita è dato dal segmento che unisce il Sole al punto 1 (sinistra) nel piano stella-Sole-punto, mentre la direzione della stella vista da punto 1 (linea azzurra) giace nel piano perpendicolare a quello precedente.

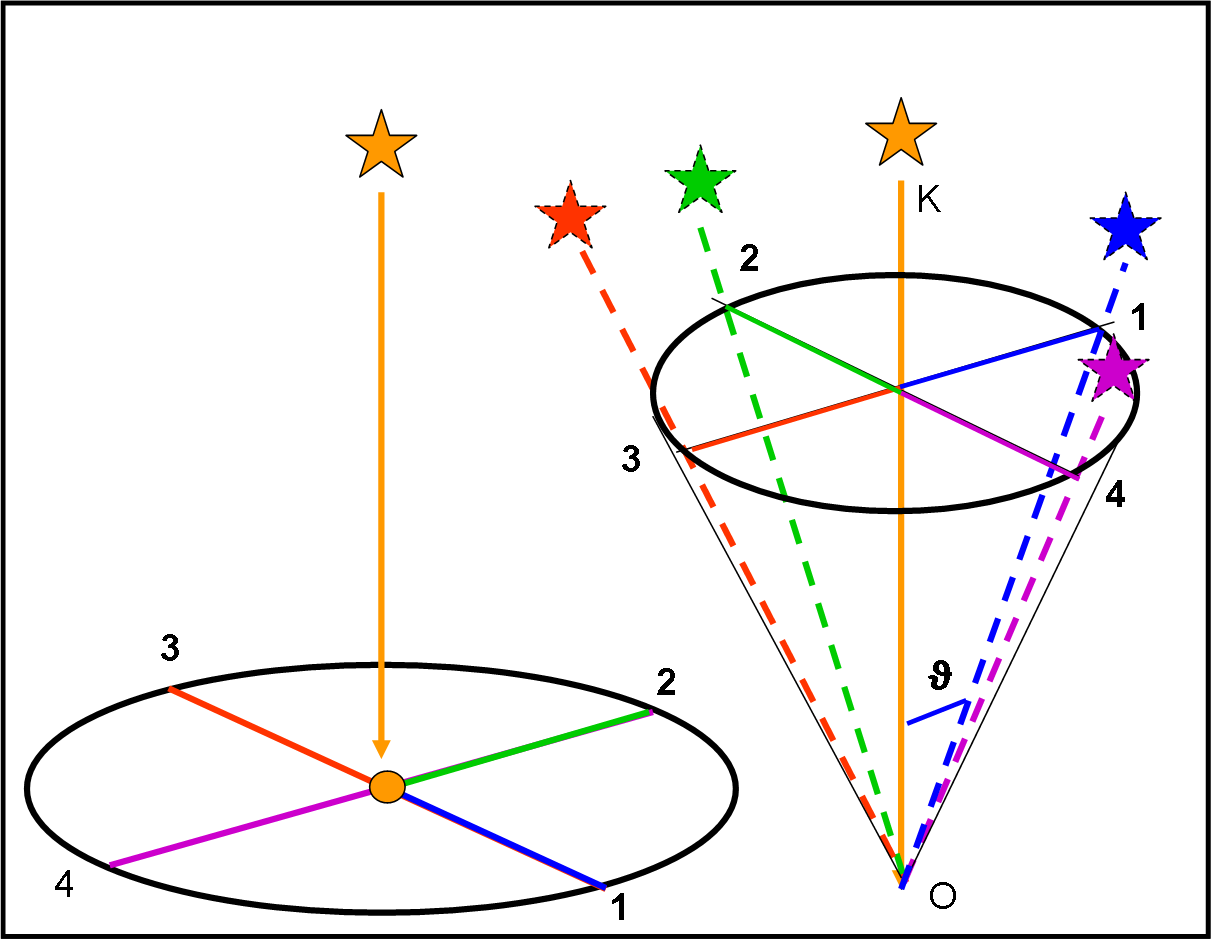
Le cose sembrano identiche alla parallasse (Fig. 13), ma sono, invece completamente cambiate. Quando l’osservatore è nella posizione 1 vede lo spostamento relativo alla direzione della stella S₁. Nella posizione 2 vede lo spostamento relativo alla direzione di S₂ e via dicendo. Tutto uguale a prima? Nemmeno per sogno: lo spostamento nel cielo avviene in una direzione che è ruotata di 90° rispetto alla posizione dell’osservatore. Infatti la Fig. 16 (che rappresenta gli effetti dell’aberrazione) non è altro che la Fig. 13 (che rappresenta gli effetti della parallasse) ruotata verso destra di 90°. Ovviamente, l'ampiezza dell'angolo del cono è decisamente diversa.

Diciamo ancora meglio: la direzione dello spostamento avviene a 90° rispetto alla direzione Sole- osservatore. Ed ecco la grande intuizione di Bradley.

La direzione Sole-osservatore è corrispondente al vettore posizione dell’osservatore 1, 2, ecc., rispetto al Sole. La direzione dello spostamento avviene, invece, secondo una direzione indicata da un vettore perpendicolare a quello della posizione. Ricordiamo che la derivata di un versore (vettore unitario, per semplicità) ha proprio una direzione a lui perpendicolare (chi vuole la dimostrazione la può trovare nell’Appendice in calce all'articolo).

Una direzione perpendicolare a quella di un versore posizione non può allora che essere la direzione derivata del versore posizione, che altro non è che il versore velocità.

Bradley conclude perciò che lo spostamento osservato della sua stella non è dovuto alla variazione lungo l’orbita della direzione della posizione dell’osservatore (come nella parallasse), ma è dovuto alla variazione della direzione della velocità dell’osservatore.

Ribadiamo ancora il concetto: quando l’osservatore è in 1 non vede la stella spostata in direzione opposta al Sole (parallasse), ma spostata in una direzione che è a 90° rispetto a quest’ultima, ossia c’è uno sfasamento di tre mesi.

Geniale, veramente geniale. La distanza della stella non c’entra niente: ciò che conta è solo la direzione della luce proveniente dalla stella rispetto alla direzione della velocità orbitale.

Analogamente a quanto trovato per la parallasse, il cerchio diventa un'ellisse sempre più schiacciata a mano a mano che la direzione della stella si abbassa verso l’eclittica. Cosa succede lo illustra la Fig. 17, da studiare con attenzione.

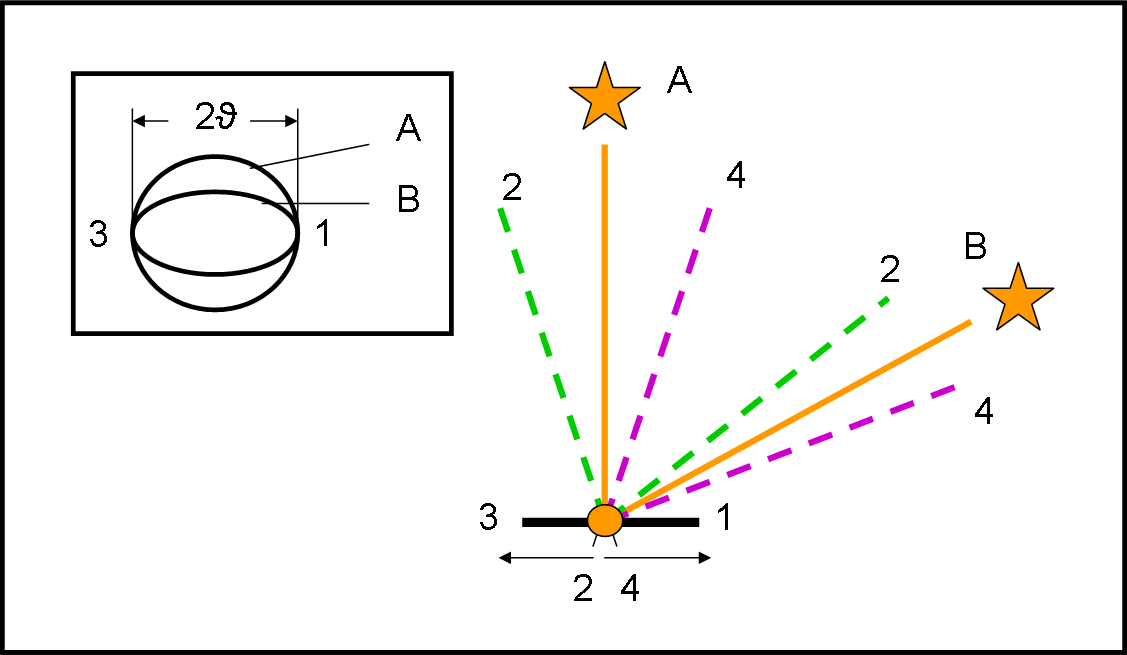
Immaginiamo di vedere di taglio l’orbita terrestre. Trovarsi nei  punti 4 e 2 dell’orbita corrisponde ad avere spostamenti della stella nelle direzioni orbitali 1 e 3 (ossia 4 e 2 sulla sfera celeste). Ciò comporta che un abbassamento verso la posizione 1 (terrestre) della stella causa una variazione degli spostamenti sulla sfera celeste nella direzione da 4 a 2. Sono proprio questi spostamenti quelli che definiscono l’asse minore dell’ellisse. Gli spostamenti lungo la congiungente 1 e 3 sulla sfera celeste rimangono quindi sempre costanti, infatti il vettore luce è sempre perpendicolare al vettore velocità in 1 e in 3 dell’orbita. Spero di essere stato abbastanza chiaro… nel caso chiedete maggiori delucidazioni.

Per una stella sull’eclittica ricadiamo nel segmento che rappresenta, comunque, il semiasse che è sempre uguale all’angolo ϑ, angolo di aberrazione. Un percorso fittizio che è uguale per tutte le stelle del cielo.

Ridendo e scherzando, il grande Bradley è riuscito a ottenere un paio di informazioni preziosissime. Innanzitutto, la soluzione del triangolo dell’aberrazione può darci facilmente il valore della velocità della luce e migliorare quello ottenuto da Romer attraverso le eclissi dei satelliti di Giove. Inoltre, e non è cosa da meno, James ha finalmente ottenuto la prova osservativa, tanto cercata da Galileo e non solo, della teoria eliocentrica.

Facciamo fatica a pensare ad Aristarco? Sono decisamente convinto che se avesse avuto la strumentazione adatta avrebbe sicuramente capito anche lui che non si trattava della tanto cercata parallasse, ma di qualcosa relativo alla velocità  di rivoluzione della Terra. E questo malgrado a quei tempi fosse molto più facile credere alle stelle fisse incastrate in una sfera ai confini del Cosmo.

Scommettiamo?

Appendice: derivata di un versore

Conosciamo i versori (QUI) e li usiamo dato che non si portano dietro nessun modulo (sono unitari).

Eseguiamo il prodotto scalare di due versori:

v x v = |v|² = 1

v x v = 1

Deriviamola…

dv/dt x v + v x dv/dt = 0

2 v x dv/dt = 0

v x dv/dt = 0

Sappiamo che il prodotto scalare di due vettori è uguale a zero solo se i due vettori sono perpendicolari, il che vuole anche dire che la derivata del versore è perpendicolare al versore stesso.

CVD (Come Volevasi Dimostrare...)