Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Approfittiamo di un racconto mitologico greco per dare un’altra versione facilitata dell’aberrazione della luce, capace, però, di introdurci nei due  sistemi di riferimento necessari  e calcolarla sia in modo classico (prima) che relativistico (dopo).

Sappiamo tutti benissimo quanto siano state importanti le due città-stato greche, Atene e Sparta. Purtroppo, le due città ebbero sempre una grande rivalità che le portò a guerre cruenti. Pochi, però, sanno che una delle guerre più violente si ebbe per colpa…. dell’aberrazione annua o qualcosa di molto simile.

I greci sapevano tante cose sui corpi celesti, ma questo fenomeno gli era sconosciuto per molteplici motivi. E così accadde il gravissimo fatto di Belmina. La storia si mischia alla mitologia, ma non è ancora chiaro se ci sia stato un vero inganno o se entrambi i personaggi chiave fossero in buona fede. Cosa, questa, difficile da credere, ma con gli dei burloni di quei tempi tutto era possibile. Giove, da buon capo della brigata, se ne lavò le mani e mai rivelò la verità.

Era da poco finita la guerra che Sparta aveva vinto contro Argo, ma Atene non era stata da meno e aveva sedato con prontezza una ribellione della regione settentrionale fomentata dai persiani. Entrambe le città erano quindi convinte di meritarsi un premio divino. Giove accolse la richiesta e decise di regalare un diamante di grandezza e splendore mai visti a una delle due città. Sì, ma a quale città? Come detto, nessuno lo saprà mai…

Casualmente (ma sarà vero?), due importantissimi uomini di stato, uno ateniese e uno spartano, si trovarono contemporaneamente nei pressi della piccola città di Belmina, ai confini dei due stati, in un momento di pace molto precaria. Poche decine di metri dividevano i due dignitari.

Improvvisamente, sopra una nuvola, apparve Giove in persona e la sua voce tonante rimbombò per chilometri e chilometri: “Il vostro gesto impavido merita un regalo. Eccovi il più gran diamante che mortale abbia mai visto. Sia costruito un tempio in mio nome per conservarlo a memoria futura”. Al breve discorso seguì il lancio del diamante. Così come era apparso, Giove scomparve alla vista dei mortali. Aveva molto da fare con una bella popolana e non sapeva ancora in che animale trasformarsi…

Il diamante iniziò il suo viaggio verso terra ed entrambi i dignitari si convinsero che il regalo era per loro. Sì, ma per uno solo di loro. A insaputa uno dell’altro tirarono fuori una coppa capiente e attesero il dono divino con orgoglio e devozione.

Lo spartano aveva una coppa nera e l’ateniese una coppa rossa. Alla fine, fu l’ateniese a ricevere il regalo, ma entrambi si scagliarono contro l’avversario accusandolo di furto e di tentato furto.

In particolare, l’ateniese disse che mentre lui stava tranquillamente aspettando l’arrivo del diamante, lo spartano corse verso di lui e cercò di mettere la coppa davanti alla sua. Con prontezza lui riuscì a ricevere il dono come era stato stabilito dal Giove, ma proprio per un pelo…

La versione dello spartano fu invece completamente diversa. Mentre lui aspettava il dono con le lacrime agli occhi per la gioia, l’ateniese gli corse incontro e riuscì a inserire la coppa sopra la sua e rubare il regalo di Giove.

Una situazione ambigua e praticamente irrisolvibile. Chi aveva ragione? (Non vi ricorda un poco il celebre e bellissimo film di Akira Kurosawa, “Rashomon”, o la revisione western, “L’oltraggio”, con Paul Newman?)

La Fig. 25 descrive le due versioni.

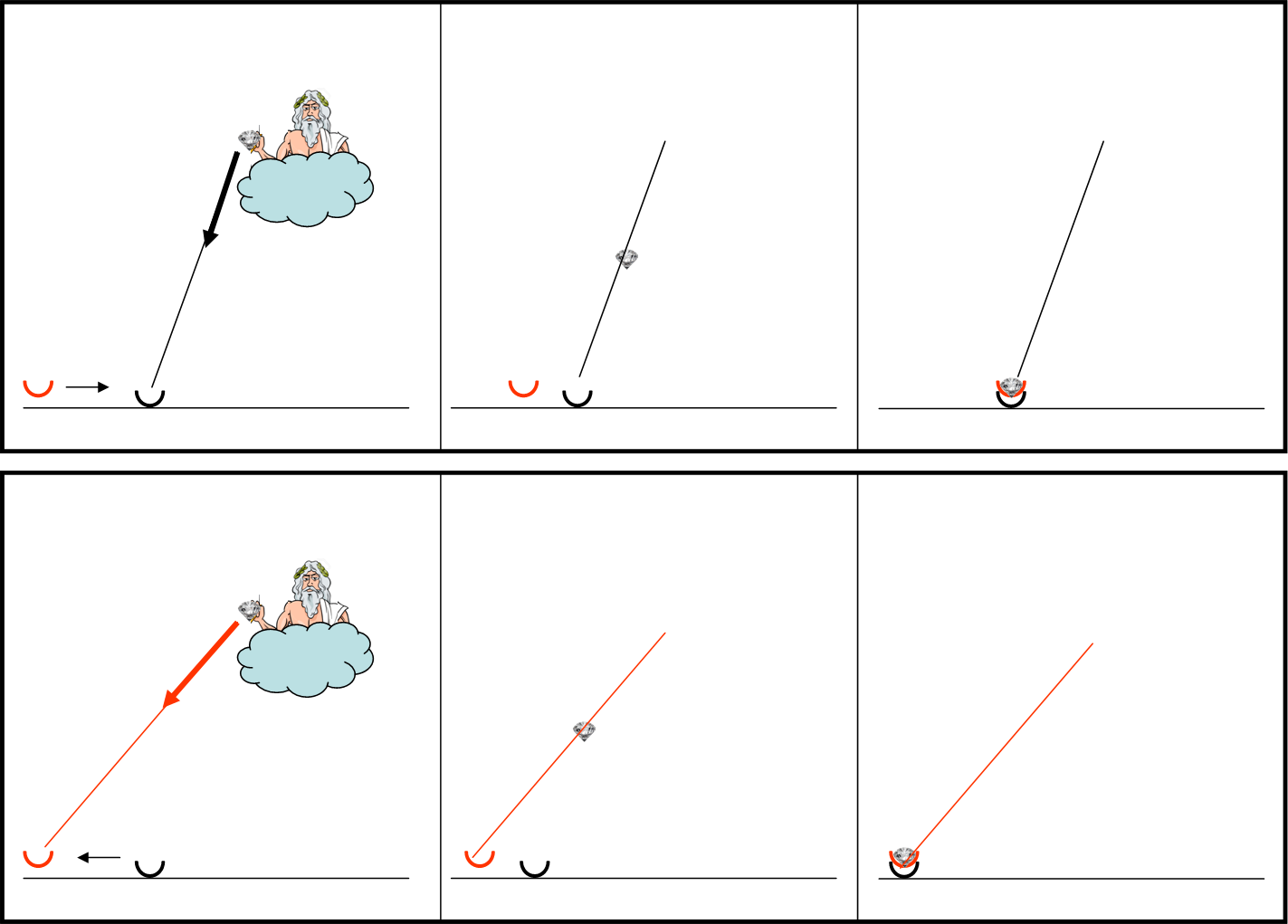
In alto, quella dello spartano. Giove lancia il diamante verso di lui (coppa nera), ma l’ateniese corre velocemente incontro allo spartano e al momento dell’arrivo del diamante riesce a inserire la sua coppa davanti a quella dello spartano. Un vero furto!

In basso, nella stessa figura, vi è la versione ateniese.  Lui è fermo in attesa del dono ed ecco che lo spartano arrivando di corsa cerca di portarglielo via, senza riuscirci. Un tentativo di furto, evitato quasi per miracolo.

La conclusione fu una guerra terribile e mai si seppe  la versione veritiera.

Ovviamente, la storia raccontata vede sicuramente un personaggio bugiardo, dato che si svolge sulla Terra, ossia su un sistema riferimento uguale per entrambi i dignitari. Potrebbe, però, essere facilmente trasportata in campo astronomico e dare il via a una descrizione più accurata dell’aberrazione annua. Basterebbe dire che uno dei due dignitari si trovava nel sistema solidale col Sole e uno nel sistema solidale con la Terra. Non sapendo chi era quello “solare”, entrambe le versioni possono essere ugualmente veritiere ed è impossibile stabilire quale versione è quella vera, dato che lo possono essere entrambe. Con gli dei di quei tempi... tutto era possibile.

Si potrebbe anche dire, in altre parole: entrambi potrebbero essere convinti di non essersi mossi e quindi ognuno avrebbe visto le cose pensando di essere fermo.

Le due versioni sono riassumibili facilmente con la Fig. 26.

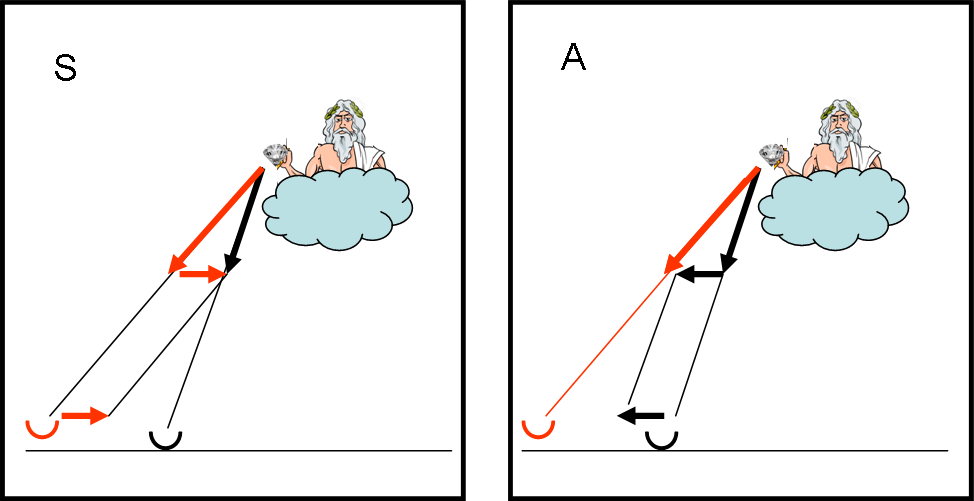
A sinistra vi è la versione spartana; a destra quella ateniese. Basta imporre una velocità di spostamento uguale e contraria per dare ragione a uno o all’altro. Tutto si capisce con un semplice triangolo composto dai vettori velocità (quelle del diamante e quella del dignitario). Ma andiamo avanti con calma.

Rivediamo l’intera scena, secondo le due versioni, applicando pari pari i concetti usati per l’aberrazione annua. Per comprendere al meglio la similitudine, invece di una coppa, i due dignitari usano due lunghi tubi, che tanto assomigliano ai telescopi usati nell’articolo precedente (QUI).

Iniziamo dalla Fig. 27a (in alto), con la versione dello spartano.

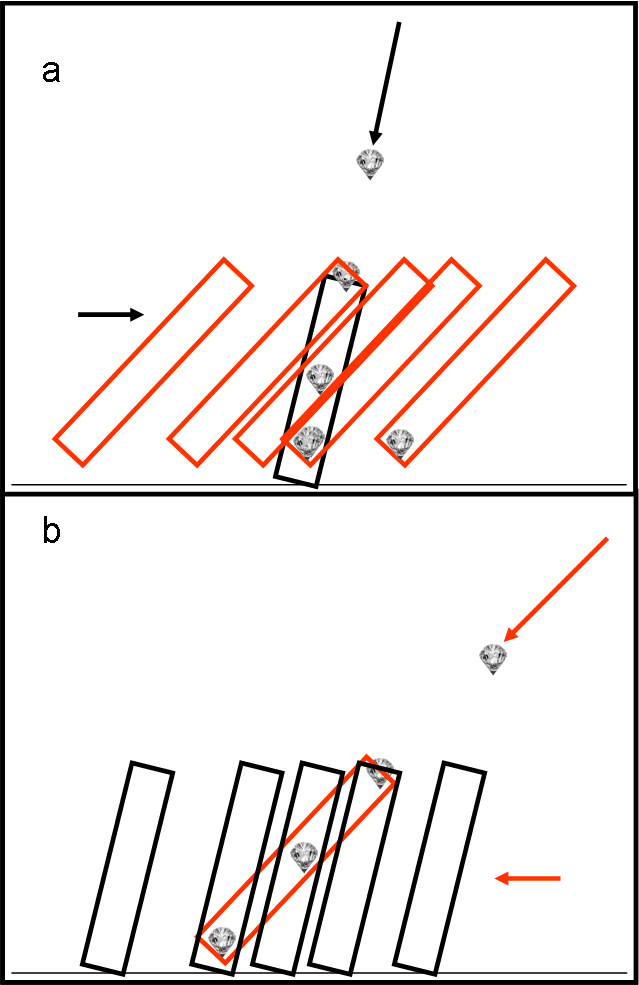
Egli è nel sistema del Sole ed è convinto (giustamente) di non muoversi e vede il diamante venire verso di lui. L’ateniese con il suo tubo rosso arriva nel momento giusto per fare il furto solo perché  sta muovendosi con la Terra, mentre lo spartano no. Il tubo nero è sempre lo stesso, dato che è fermo. Quello rosso invece si muove con la Terra. I vari tubi rossi si riferiscono a istanti successivi e vanno visti da sinistra verso destra. Quando il diamante arriva all’entrata del tubo nero, vi giunge anche il tubo rosso. La sua inclinazione permette al diamante di cadere completamente all’interno del tubo rosso che può trascinarselo via con sé. Un vero furto per lo spartano.

Attenzione! L’inclinazione deve essere proprio quella giusta, ossia quella che risulta dalla combinazione delle velocità. Se l’inclinazione fosse diversa il diamante non arriverebbe fino in fondo al tubo rosso, ma, dato il suo peso, lo bucherebbe e cadrebbe in quello nero (Fig. 28)

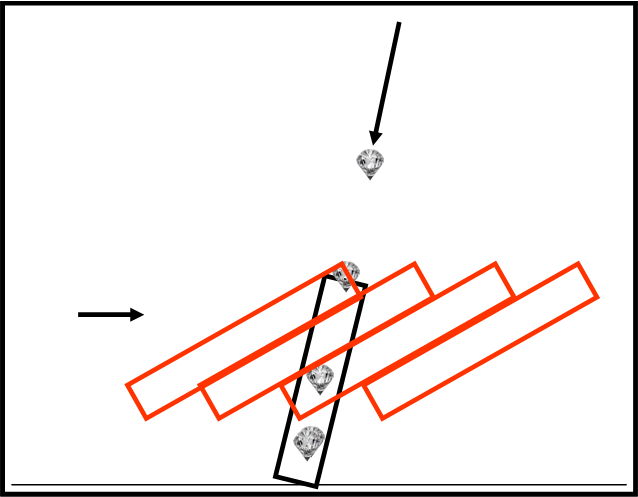
In Fig. 27b (in basso) abbiamo la versione dell’ateniese. Lui si sente fermo (e ci crede veramente). Il suo tubo è inclinato e attende l’arrivo del diamante che appare proprio andare verso di lui. Questa volta è lo spartano che appare muoversi verso sinistra. Quando il suo tubo arriva esattamente a toccare il diamante potrebbe benissimo essere lui a rubarlo all’ateniese e se non ci riesce è solo per l’abilità di quest’ultimo di anticiparlo di una frazione di secondo. Tuttavia, la direzione del tubo nero sarebbe perfetta per rubare il diamante.

Descritta in questo modo, si vede benissimo che l’avventura mitologica rispecchia perfettamente la spiegazione data con il telescopio e la posizione diversa della stella tra un osservatore eliocentrico e uno terrestre.

Possiamo, allora, permetterci di semplificare geometricamente la situazione e utilizzare due sistemi di riferimento in moto relativo e descrivere la composizione delle velocità che ne deriva. Prima lo faremo in modo classico e poi non avremo alcun problema a metterci nella RR.

Disegniamo la Fig. 29 che riassume la configurazione quando entrambi i telescopi abbiano lo stesso punto O al centro del loro obiettivo (il momento del furto…).

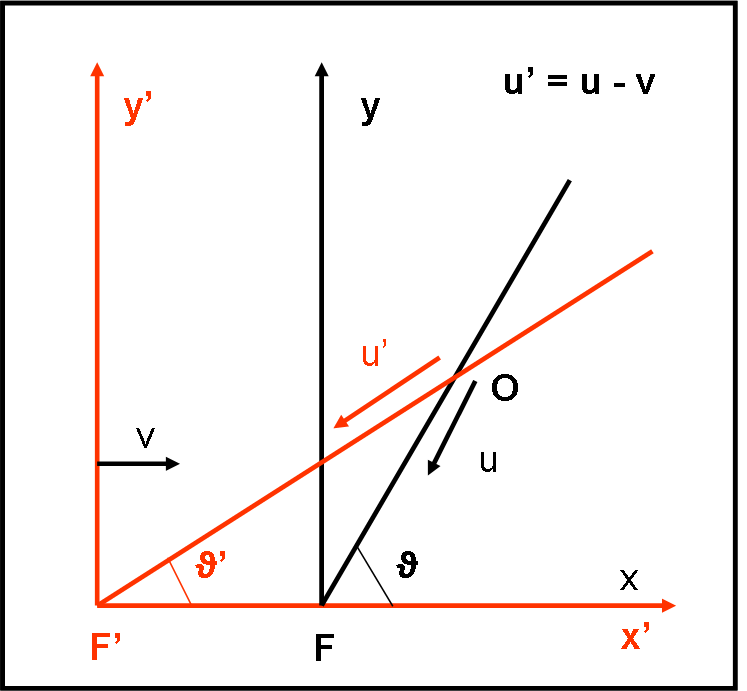
Essendo nel caso classico, possiamo scrivere la relazione:

u’ = u – v

Dove v è la velocità con cui il sistema dell’ateniese (Terra) si muove verso destra. La velocità del diamante vista nel sistema dello spartano (Sole, ossia fermo) è u, mentre u’ è la risultante come appare nel sistema della Terra. Le due direzioni delle velocità (ossia il moto del diamante) sono viste dai due fuochi dei telescopi con angoli ϑ e ϑ’.

Notiamo che continuiamo a usare una velocità u, che nel caso della luce dovrà essere rimpiazzata da c. Tuttavia, dato che dobbiamo sommare vettori è meglio, per adesso, non fare entrare c, dato che sembrerebbe darci valori maggiori di quelli della luce… Continuiamo, perciò, con una qualsiasi velocità u, quella alla portata di … Giove.

Lasciamo passare un po’ di tempo fino a che F’ coincida con F e disegniamo di nuovo la configurazione in Fig. 30, inserendo, questa volta, le velocità con la loro reale intensità. Otteniamo un bel triangolo da studiare con attenzione. Gli angoli sono sempre gli stessi, ovviamente.

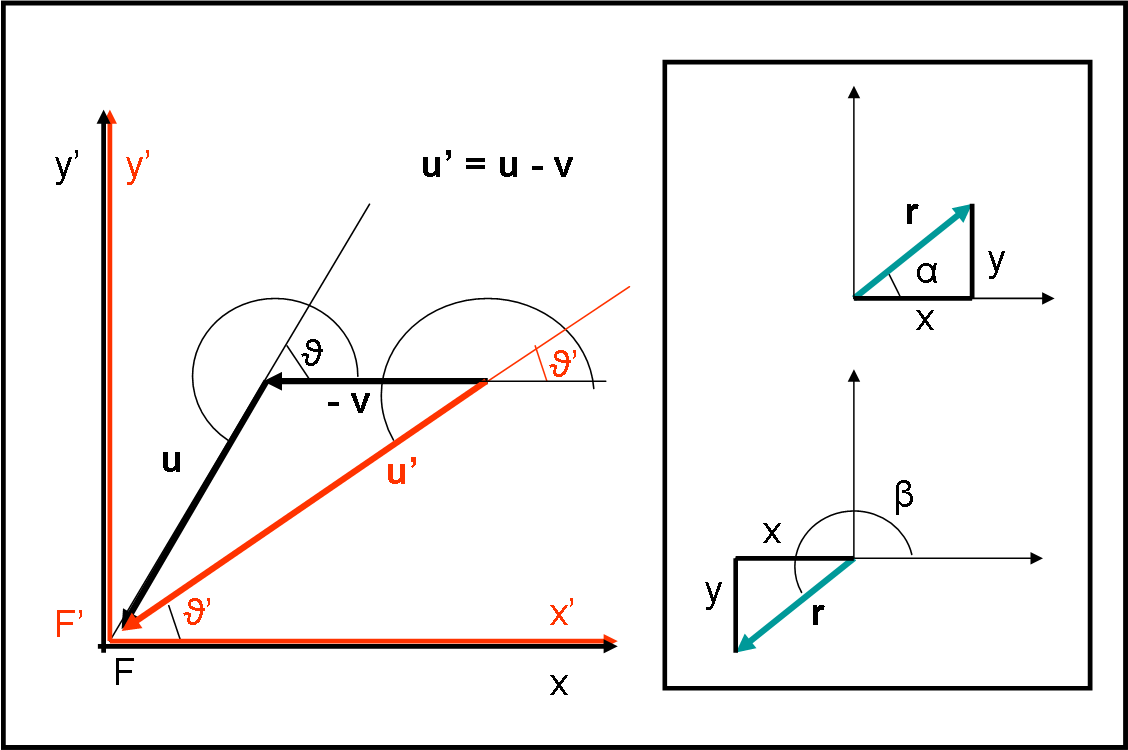
Soffermiamoci sul riquadro di destra. Sono cose che dovremmo sapere, ma è meglio richiamarle…

Come si fanno a trovare le componenti di un vettore lungo due assi cartesiani? Beh… basta usare le coordinate polari (ad esempio, QUI, Fig. 1):

se r è il vettore blu della parte alta, le sue coordinate sono

x = r cos α

y = r sen α

Ma, se portiamo il vettore r dalla parte opposta, ruotandolo di 180° (parte bassa), possiamo ancora scrivere le stesse relazioni? Sicuramente sì, dato che esse devono valere per qualsiasi angolo. Possiamo scrivere tranquillamente:

x = r cos β = r cos (α + 180) = - r cos α

y = r sen β = r cos (β + 180) = - r cos β

Abbiamo fatto un paio di passaggi estremamente banali, ma è meglio richiamarli dato che ci serviranno molto presto.

Torniamo al nostro triangolo, composizione di vettori velocità.

La relazione

u’ = u – v

può essere scritta attraverso le sue componenti secondo gli assi x e y.  Facendo ciò, tratteremo con vettori che hanno la stessa direzione e quindi possiamo utilizzare solo il loro modulo.

Iniziamo con le componenti secondo l’asse x’ che coincide con x:

u’ cos(180 + ϑ’) = u cos(180 + ϑ) – v cos(0)

- u’ cos ϑ’ = - u cos(ϑ) – v

 u’ cos ϑ’ =  u cos(ϑ)  + v             …. (14)

Abbiamo subito capito perché sono state richiamate le componenti con angoli maggiori di 180° …

Passiamo alle componenti secondo y’ coincidente (o, più in generale, parallelo a y):

u’ sin (180 + ϑ’) = u sin (180 + ϑ)

- u’ sin (ϑ’) = - u sin (ϑ)

 u’ sin (ϑ’) = u sin (ϑ)                 …. (15)

Facendo il rapporto tra la (14) e la (15) si ottiene:

u’sin ϑ’/ u’cos ϑ’ = u sin ϑ/(u cos ϑ  + v)

Semplificando e dividendo numeratore e denominatore del secondo membro per u, si ha:

sin ϑ’/cos ϑ’  = sin ϑ/(cos ϑ + v/u)      …. (16)

tan ϑ’  = sin (ϑ)/(cos(ϑ)  + v/u)        …. (17)

Questa è la relazione accurata che lega l’angolo sotto cui viene vista una stella dal Sole con quello visto dalla terra, inclinato a causa dell’aberrazione. Si nota bene che compare solo u che può benissimo essere sostituita con la velocità della luce c. Inoltre, questa formula permette di ricavare immediatamente di quanto va inclinato l’angolo visto da chi si muove (ϑ’) rispetto a quello visto da chi è in quiete. E questa possibilità è importantissima per affrontare il viaggio in astronave.

Si può anche ricavare, facilmente, la formula che abbiamo trovato precedentemente (QUI), introducendo la costante di aberrazione  K = v/c.

Dalla (16) si ha:

sin ϑ’ (cos ϑ + v/c)= sin ϑ cos ϑ’

sin ϑ’ cos ϑ + v/c sin ϑ’ = sin ϑ cos ϑ’

sin ϑ’ cos ϑ - sin ϑ cos ϑ’ = - v/c sin ϑ’

Sappiamo però che vale la relazione trigonometrica (QUI, appendice)

sen (ϑ’ - ϑ) = sin ϑ’cos ϑ -  cos ϑ’ sen ϑ

Da cui, sostituendo:

sen (ϑ’ - ϑ) = - v/c sin ϑ’

sappiamo anche che sen (-α) = - sen α, e quindi:

- sen (ϑ – ϑ’) = - v/c sin ϑ’

sen (ϑ – ϑ’) =  v/c sin ϑ’ = K sin ϑ’

E con le approssimazioni fatte, lavorando con le coordinate celesti (QUI):

ϑ – ϑ’ = K sin ϑ

Torniamo, adesso, alla nostra formula generale, ma  toccherà a voi...