QUIZ: una richiesta assurda? ***(*)

10/02/17

QUIZ: una richiesta assurda? ***(*)

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:19

Non vorrei sembrare troppo arrogante… ma, questa volta, l’apprendista stregone cerca di sfidare il club dei maghi (ma non solo loro). Abbiamo bisogno soltanto di una circonferenza e di un triangolo equilatero. I procedimenti per ottenere la soluzione sono molti e quindi potrebbe diventare un  vero "tormentone", come già successo per altri quiz.

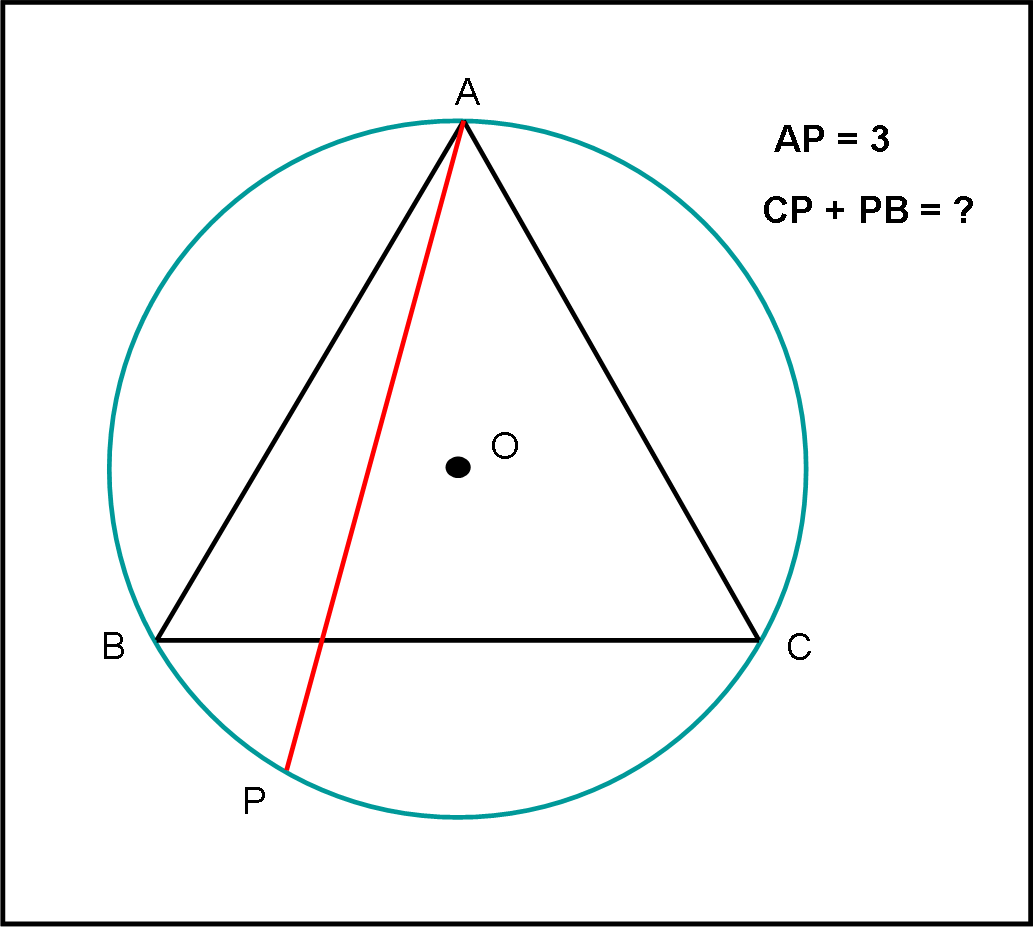
Nella figura che segue vi è un triangolo equilatero ABC inscritto in una circonferenza di centro O.

triangolo

Consideriamo un punto P sull’arco BC, tale che:

AP = 3

Chiediamo “semplicemente”:

Quanto vale BP + PC ?

A prima vista sembrerebbe una domanda assurda, dato che non si conosce il raggio della circonferenza e … invece il problema è risolvibile in vari modi (almeno 5, ma probabilmente anche di più).

Una richiesta supplementare: se, durante il procedimento, ci fosse bisogno di utilizzare qualche teorema poco conosciuto, sarebbe bene darne la dimostrazione. Una ghiotta occasione per richiamare qualche teorema geometrico dimenticato.

Anche questo simpatico gioco potrebbe richiamare il genio degli antichi greci…

Buon divertimento e non abbiate paura a provare. Magari scopriremo un nuovo … mago!

Soluzione QUI

Articoli correlati

19 commenti

  1. Arturo Lorenzo
    10/02/2017 at 20:52

    Purtroppo mi trovo ancora al lavoro e da qui non posso caricare un' immagine (peraltro già pronta), lo farò appena tornato a casa.

    Quindi perdonatemi se la mia risposta sarà per ora solo testuale.

    Ho risolto il quiz per via praticamente solo grafica. La risposta al quiz è 3.

    Traccio la retta passante per P e per C . Faccio centro in P e traccio l'arco di circonferenza che interseca la suddetta retta nel punto che chiamo K. Traccio il segmento AK. Se la figura è stata disegnata correttamente, salta subito agli occhi che il triangolo ACK sembra uguale al triangolo ABP. Vediamo se è davvero così.

    Questi due triangoli hanno :

    • il lato AC congruente al lato AB. Infatti AC e AB sono due lati del triangolo equilatero di partenza ABC.
    • il lato AK congruente al lato AP, cioè pari a 3. Qui la spiegazione è più lunga. L'angolo APC è angolo alla circonferenza della corda AC, la quale, essendo lato di un triangolo equilatero inscritto in una circonferenza, sottende un angolo al centro di 120 gradi. Per cui, essendo l'angolo alla circonferenza sotteso da una corda pari alla metà dell'angolo al centro sotteso dalla stessa corda, abbiamo che l'angolo APC è di 60 gradi. Siccome , poi, per costruzione, il lato AP è congruente al lato PK, abbiamo che il triangolo APK è isoscele con angolo al vertice di 60 gradi, per cui anche i due angoli uguali alla base saranno di 60 gradi. Quindi, in definitiva, il triangolo APK è equilatero, per cui AK = AP = 3.
    • l'angolo CAK è congruente all'angolo BAP. Infatti abbiamo che l'angolo BAP + l'angolo PAC = 60 gradi (angolo del triangolo equilatero di partenza) e che l'angolo PAC + l'angolo CAK = 60 gradi (angolo del triangolo equilatero APK. Allora , dalle due suddette relazioni deriva che l'angolo BAP = all'angolo CAK.

    Per il primo criterio di congruenza dei triangoli, quindi, i due triangoli ABP e ACK sono davvero congruenti. Quindi anche il lato CK è congruente al lato BP. Ma allora , essendo PK = PC+CK, e PK = 3, sarà PC+BP = 3

    :wink:

     

  2. Arturo Lorenzo
    10/02/2017 at 21:05

    ecco la figura

     

  3. maurizio
    11/02/2017 at 02:39

    Questa è una delle altre possibili soluzioni...

    Osservo che quando il punto P è in B   la  somma   b+c  è uguale ad   a   (coincidente con il lato del triangolo),     specularmente , se  P è in C ,     b+c=a.

    Nella posizione intermedia, quando P si allinea con O A,  dai due triangoli  BAP  e  PAC  vedo che b=c= AP/2, quindi anche in questo caso la somma  b+c  è uguale ad a.

    Verifico che in posizioni generiche b+c sia sempre = a  esprimendo tutto in funzione dell'angolo alfa e del lato del triangolo equilatero   l

    a= l cos(30-alfa) = l (cos 30 cos alfa  + sen 30 sen alfa) = l cos alfa cos 30 + (l sen alfa)/2

    b= l sen alfa

    c=l sen(60-alfa) =  l (sen 60 cos alfa - cos 60 sen alfa)

    b+c = l sen alfa (1-cos60) + l cos alfa sen 60  =  l (sen alfa)/2 + l cos alfa cos 30   =  a

    Per qualsiasi valore di alfa e di l risulta quindi  b+c=a

    Considerando che i quattro punti ABCP si trovano su una conica, mi domando se non sia possibile trovare una soluzione anche  attraverso le proprietà del birapporto armonico , ma dovrei ricordarmi qualcosa di più della geometria proiettiva.

     

     

     

     

     

  4. Vincenzo Zappalà
    11/02/2017 at 05:59

    cari maghi...

    come al solito siete rapidissimi. Tuttavia, le possibilità sono ancora tante, anche senza le armoniche...

    Volevo solo far presente un punto fondamentale (che può essere aiuto di anche per altri). A prima vista la soluzione sembrerebbe impossibile per carenza di informazioni. Ciò che bisogna fare, allora, è trovare una soluzione limite e poi cercare di dimostrare che la soluzione limite è l'unica soluzione plausibile, ossia che è un invariante. I nostri amici sembra proprio che non abbiano avuto dubbi a seguire questa strada. Forza... si può ancora fare meglio...o -almeno- in modo più elegante (forse) e senza tutti quei brutti seni e coseni.... :mrgreen:

  6. maurizio
    11/02/2017 at 16:03

     

     

     

     

  7. Vincenzo Zappalà
    11/02/2017 at 16:35

    scusa Maumau... ma è un problema spiegare bene cosa hai fatto? Spiega bene cosa hai costruito e perché certi segmenti sono uguali. Proprio tu che usi tanto le (belle) parole, ti sei messo a tacere????!!!! Cerca di essere... logorroico! :mrgreen:

  8. maurizio
    11/02/2017 at 17:49

    Ciao Vince, ho lasciato Pautasso da solo davanti al  PC e ha fatto tutto lui...

    Comunque adesso ti metto in comunicazione....

    "Buongiorno Prof. Zappala, dunque....spiego come  ho costruito l'ultima figura.

    Le linee in bianco sono quelle assegnate nel problema: il triangolo equilatero e anche la retta che passa per P.

    Le corde BP (in giallo) e PC (in rosso) sono quelle di cui si chiede "semplicemente" , come dice lei, il valore della somma.

    Su ciascun lato del triangolo equilatero riporto queste corde (vedete che le linee conservano il loro colore giallo e rosso).

    A questo punto ho disegnato un esagono  i cui vertici, in senso antiorario, a partire dal punto P sono  i seguenti:  PCP'AP''B  questo esagono è composto da lati alternati gialli e rossi.

    Infine collego B con P' (linea blu)  e C con P'' (linea verde).

    Osservate il lato PC:   da P e da C sono tracciati i due lati  (gialli) PB e CP' , uguali per costruzione.             Questo significa che BP' è parallelo a PC.

    (Con analogo ragionamento si può dire che   AP (bianco)  è  parallelo P''B  e  che  P''C (verde)  è  parallelo a AP'

    Ecco  ora lo stesso disegno con una piccola aggiunta...

                                                                                                                                                                                                                           
    Data la simmetria della figura è evidente che se traslo  il segmento P'C (giallo) su AP, va  a sovrapporsi a QP.

    Allo stesso modo il segmento  BP''(rosso)  va a sovrapporsi ad AQ

    La lunghezza di AP equivale  quindi a "un giallo + un rosso" cioè BP (giallo)+PC(rosso).

    Se AP vale 3, anche BP+PC vale tre.

    Sa AP vale un qualsiasi valore , BP + PC varrà comunque il medesimo valore.

     

    Nel post antecedente (quello in cui il cerchio ha uno sfondo verde ) la costruzione non si sviluppa sui tre lati del triangolo equilatero dato, ma solo su due. Si possono individuare i triangoli equilateri BQP  e  AQP'  che consentono le seguenti affermazioni : BP=PQ  e QA=AP'

    Quindi  AP =  PQ+ QA  =  BP+AP'.  ma AP'=PC (sempre per costruzione),  per cui: AP=  BP+PC  con le stesse conclusioni già viste.

    Reverenti ossequi a tutti i lettori"

    Oreste Pautasso

     

     

     

  9. Vincenzo Zappalà
    11/02/2017 at 18:23

    Bravo Pautasso,

    così va meglio... ma direi con qualche parola perché i triangoli che trovi alla fine sono anche loro equilateri... su, non farti tirare fuori  le parole.

    Non male, direi... ma un po' troppe costruzione aggiuntive... forse se ne può fare a meno e NON costruire niente di più. Basta ricordare un teorema.... :wink:

  10. maurizio
    11/02/2017 at 19:08

    parliamo dei triangoli equilateri :  ABC è un dato del problema.

    Gli angoli BAP , CBP' e CAP'   sono uguali perché su corde uguali.

    Quindi i lati del triangolo AQP formano tra loro gli stessi angoli di ABC, ossia il triangolo  AQP è equilatero.

    L'angolo BQP è opposto al vertice a AQP' quindi è di 60° Inoltre AP=BP' (su archi uguali ABF= BCP') , quindi  essendo QA = QP'  ne consegue BQ=PQ.

    Anche il triangolo BQP è equilatero (angolo 60° e due lati che lo comprendono uguali).

    Ci sono sicuramente  diversi altri modi per dimostrarlo.

  11. Arturo Lorenzo
    11/02/2017 at 20:20

    dimostrazione alternativa del risultato pari a 3, caso generale, riferimento alla figura da me pubblicata nel secondo commento di questo quiz .

    Indico con \alpha l'angolo BAP e con \beta l'angolo PAC. Evidentemente risulta, per costruzione:

    \alpha +\beta =60

    Ora:

    per il teorema dei seni ( e tenendo presente che una stessa corda sottende sempre lo stesso angolo alla circonferenza, ovunque si ponga il suo vertice sulla circonferenza) :

    \frac{BP}{sen(\alpha )}=\frac{AP}{sen(\beta +60)}

    che, svolgendo i calcoli, restituisce:

    BP=3\frac{sen(\alpha )}{\frac{\sqrt{3}}{2}cos(\alpha )+\frac{1}{2}sen(\alpha )}          (1)

     

    poi, sempre per il teorema dei seni:

    \frac{PC}{sen(60-\alpha )}=\frac{AP}{sen(60+\alpha)}

    che, svolgendo i calcoli. restituisce:

    PC=3\frac{\frac{\sqrt{3}}{2}cos(\alpha )-\frac{1}{2}sen(\alpha )}{\frac{\sqrt{3}}{2}cos(\alpha )+\frac{1}{2}sen(\alpha )}         (2)

     

    andando a sostituire la (1) e la (2) nella somma BP+PC, alla fine, fatti i calcoli (che ometto per brevità) , ottengo proprio 3  :-D

     

     

     

  12. maurizio
    11/02/2017 at 20:24

    Ciao Lorenzo, a me piace anche questa tua estensione, ma se guardi il commento di Enzo, di questa mattina alle sei.....

    Forza... si può ancora fare meglio...o -almeno- in modo più elegante (forse) e senza tutti quei brutti seni e coseni.... :mrgreen:

     

    Comunque c'è sempre la chirurgia plastica...

  13. Arturo Lorenzo
    11/02/2017 at 20:41

    Ciao Maurizio,

    io sono partito con sola grafica e primo criterio di congruenza dei triangoli, poi mi è venuta in mente quest'altra via con il teorema dei seni. Però, alla fine, dove dico di avere omesso i calcoli per brevità, in realtà i seni e coseni si semplificano , perché l'espressione del numeratore risulta uguale a quella del denominatore. E così resta solo il 3.

    Però, obiettivamente, è più bella la via grafica. La verità che cerchiamo, molto spesso, aspetta solo di essere vista nel modo giusto  :wink:

  14. Arturo Lorenzo
    12/02/2017 at 14:32

    sempre per via grafica e utilizzando il primo criterio di congruenza dei triangoli:

    Mando da C la retta parallela al segmento BP. Tale retta interseca in T il segmento AP. Considero il triangolo PTC. L'angolo CPT è di 60° perchè sotteso dalla corda AC (che è anche lato del triangolo equilatero ABC). L'angolo PTC è congruente all'angolo BPA perché alterni interi di rette parallele tagliate dalla trasversale PA. L'angolo BPA a sua volta è uguale a 60° perché sotteso dalla corda AB (che è anche lato del triangolo equilatero ABC). Quindi l'angolo PTC è uguale anch'esso a 60°. Allora, per somma degli angolo interni di un triangolo pari a 180°, anche l'angolo PCT è uguale a 60°. Pertanto il triangolo PCT è equiangolo e quindi equilatero.

    Considero ora i triangoli rosso e verde. Per essi risulta

    1. AC \cong BC per costruzione
    2. TC \cong PC perché PCT triangolo equilatero
    3. angolo ACT  \cong  angolo BCP  perché ACT+TCB\cong 60° e TCB+BCP \cong 60°, da cui, sottraendo membro a membro si ottiene ACT \cong BCP

    Pertanto, per il primo criterio di congruenza dei triangoli, i triangoli rosso e verde sono congruenti, quindi:

    BP\congTA

    Ma allora:

    PA\congPT+TA\congPC+BP

    quindi

    PC+BP=3

     

     

  15. Vincenzo Zappalà
    12/02/2017 at 17:46

    bene, bene... ma io mi tengo da parte il teoremino (sapendo quello tutto è immediato!). Poi, magari, lo dimostriamo anche... Che bella la geometria e quanto erano bravi i greci!!!

  16. Arturo Lorenzo
    12/02/2017 at 20:07

    OK, allora passiamo ai criteri di similitudine...

    Consideriamo i triangoli ABP e RPC

    Tali triangoli sono simili per i primo criterio di similitudine. Infatti:

    angolo BAP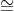 \cong angolo RCP perché sottesi dalla stessa corda BP

    angolo BPA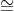 \cong angolo RPC perché BPA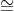\cong60° (angolo sotteso dalla corda AB che è lato del triangolo equilatero inscritto) e RPC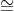\cong60° (angolo sottesso dalla corda AC che è lato del triangolo equilatero inscritto)

    angolo ABP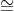 \cong angolo PRC perché supplementari di una stessa somma di angoli

    Quindi, essendo i due suddetti triangoli simili, posso scrivere:

    \frac{AP}{PC}=\frac{AB}{RC}

    da cui ricavo RC:

    RC=\frac{AB}{AP}*PC           (1)

    Passo ora a considerare i due triangoli BRP e APC.

    Anche questi sono simili per il primo criterio di similitudine. Infatti:

    angolo RBP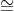 \cong angolo PAC perché sottesi dalla stessa corda PC

    angolo BPA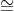 \cong angolo RPC 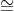\cong 60° per quanto detto prima

    angolo BRP \cong angolo ACP perché supplementari di una stessa somma di angoli

    Essendo simili, posso allora scrivere:

    \frac{BR}{AC}=\frac{BP}{AP}

    da cui ricavo BR:

    BR = \frac{BP}{AP}*AC          (2)

    Ora, dalla (1) e (2), sommando membro a membro, ottengo:

    RC+BR=\frac{AB}{AP}*PC+\frac{BP}{AP}*AC

    cioè:

    AC=\frac{AB}{AP}*PC+\frac{BP}{AP}*AC

    da cui, essendo AC \cong AB (lati del triangolo equilatero ABC) e moltiplicando tutto per AP, ottengo:

    AP=PC+BP

    cioè, in definitiva,

    BP+PC=3

    :-D

     

     

     

  17. Vincenzo Zappalà
    13/02/2017 at 05:04

    Bravo Arturo... praticamente  hai dimostrato il teorema...  :-P

  18. Arturo Lorenzo
    13/02/2017 at 08:10

    Devo ammettere che applicando il teorema di Tolomeo "in un quatrilatero inscritto in una circonferenza, la somma dei prodotti dei lati opposti è uguale al prodotto delle diagonali", il quiz si risolve in un attimo.

    Il sistema tolemaico stavolta sarebbe stato vincente ... :lol:

     

  19. Vincenzo Zappalà
    13/02/2017 at 08:14

    Bravissimo Arturo... :-P

    Hai ragione... Tolomeo non era proprio uno ... stupidotto, malgrado il sistema geocentrico (che comunque era riuscito ad adattare in modo quasi perfetto alle osservazioni).

    Stavo proprio scrivendo la soluzione e mi hai anticipato.... che mago!!!!

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.