Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Il quiz (QUI) precedente è stato brillantemente risolto da Paolo  e non ci sarebbe nemmeno bisogno di scrivere questo articolo. Ma, dato che poi li uniremo tutti insieme, conviene riportarlo in modo canonico. Scopriamo che l'aberrazione è di per sé un fenomeno relativistico che ricade in quello classico ponendo il famoso fattore gamma uguale a 1.

Tutto sta nell'utilizzare la composizione delle velocità ( e delle loro componenti) in modo relativistico e non galileiano. Il resto sono semplici calcoli poco più che elementari. Abbiamo già ricavato le formule di composizione delle componenti di una velocità se vista da un sistema  che si muove con velocità v rispetto al primo (QUI e QUI ).

Scriviamo perciò le formule relative alle componenti nel sistema S’ (dignitario che si muove) in funzione delle componenti del sistema S (dignitario che sta fermo). La velocità relativa v è diretta lungo l’asse x, mentre la velocità u ha componenti sia in x che in y. Continuiamo a usare una generica velocità u.

u’_x = (u_x - v)/(1 - vu_x/c²)

u’_y = u_y (1 – v²/c²)^1/2/(1- v u_x /c²)

Ricordando il fattore di Lorentz:

γ = 1/(1 – v²/c²)^1/2

Possiamo scriverle:

u’_x = (u_x - v)/(1 - vu_x/c²)         …. (18)

u’_y = (1/γ)( u_y/(1- v u_x /c²))         …. (19)

Sostituiamo i valori delle componenti attraverso le coordinate polari già usate precedentemente

u_x = u cos (180 + ϑ) = - u cos ϑ

u’_x = u’ cos (180 + ϑ’) = - u’ cos ϑ’

u_y = u sen (180 + ϑ) = - u sen ϑ

u’_y = u’ sen (180 + ϑ’) = - u’ sen ϑ’

nelle (18) e (19) e si ha:

- u’ cos ϑ’ = (- u cos ϑ - v)/(1 + u v cos ϑ /c²)

- u’ sen ϑ’= (1/γ)( - u sen ϑ /(1 + u v cos ϑ /c²))

E, ancora:

u’ cos ϑ’ = (u cos ϑ + v)/(1 + u v cos ϑ /c²)

u’ sen ϑ’= (1/γ)( u sen ϑ /(1 + u v cos ϑ /c²))

Dividendo membro a membro si ottiene:

u’ sen ϑ’/u’ cos ϑ’= (1/γ)( u sen ϑ /(1 + u v cos ϑ /c²)) (1 + u v cos ϑ /c²) /(u cos ϑ + v)

tan ϑ’ = (1/γ) (u sen ϑ/(u cos ϑ + v))

tan ϑ’ = (1/γ) (sen ϑ/(cos ϑ + v/u))

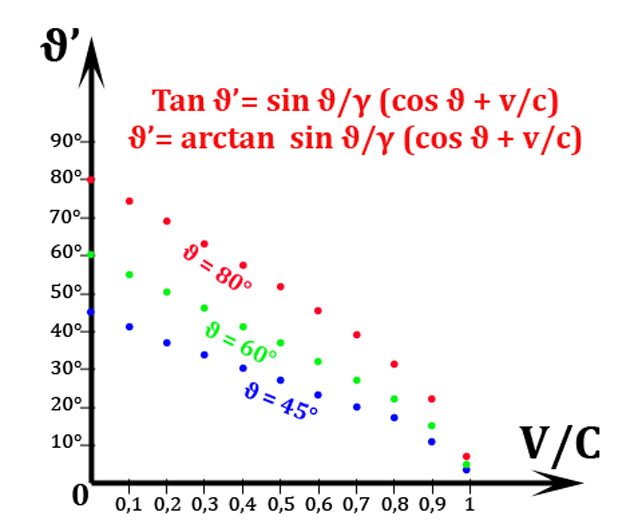
tan ϑ’ = sen ϑ/γ(cos ϑ + v/u)        …. (20)

Che diventa quella relativa alla velocità della luce (aberrazione luminosa) per v = c.

 Si nota subito che questa relazione è uguale a quella ricavata nella relatività galileiana a parte il fattore γ . Il che vuole anche dire che la formula relativistica diventa quella classica trascurando i termini di secondo ordine in v/c (la parte contenuta nel fattore γ).

La formula (20) ci permette di calcolare la deviazione del raggio luminoso come appare all’osservatore in moto più o meno rapido, qualsiasi sia la direzione della sorgente. Il tutto si risolve applicando la moltiplicazione per 1/γ in caso di velocità di movimento relativistico. A parità di angolo ϑ, l’angolo ϑ’ diventa sempre più piccolo quando si va più veloci, per sorgenti poste davanti a noi (ϑ < 90°). Questo perché 1/γ decresce al crescere di v.

Vediamo, adesso, di generalizzare il risultato e non osservare solo una stella, ma tutto il firmamento attorno a noi. Torniamo, quindi, per un poco nell’antica Grecia…

P.S.: L’immagine che segue è quella preparata con la solita bravura da Paolo per mostrare la variazione di certi angoli di incidenza al variare della velocità.