Categorie: Matematica
Tags: Club dei Maghi geometria quiz triangolo isoscele
Scritto da: Club dei Maghi
Commenti:7
QUIZ - Un angolo misterioso **/***
(IN CALCE AL QUIZ UN SUGGERIMENTO INSERITO IL 27/2/2017)
Vi proponiamo un quiz di geometria piana che ha attirato la nostra attenzione perché si presta ad essere risolto seguendo strade diverse. Anche stavolta ve lo proponiamo per mezzo del nostro simpatico amico Oreste. Eccovi la lettera che ci ha fatto pervenire....
"Carissimi Maghi e carissimo Club,
sono ancora io, Oreste Pautasso, che vi scrivo per un problema nuovo che è saltato fuori proprio ieri al C.A.C., il Centro Archeofili di Cuneo, dove svolgo la mia missione di lavoratore a pagamento.
Questi scienziati del C.A.C. hanno scoperto una figura che rappresenta la sezione trasversale di una piramide di non so quale Faraone d'Egitto e non riescono a calcolare un certo angolo misterioso.
So che siete curiosi di vedere la figura, così ve la allego, che tanto con la posta elettrica non mi costa niente.
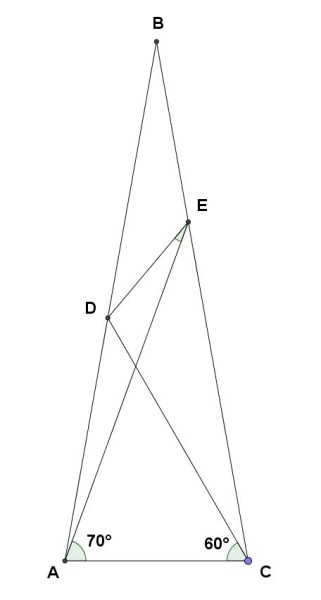
Come vedete, dentro questa piramide è come se ci fossero: il piano terra, il primo e il secondo.
Diciamo che dal punto E, in alto, entrava in certi giorni precisi un raggio di luce del sole, intrufolandosi in una fessura fatta ad' OK (non sono sicuro che si scriva così).
Questo raggio, dopo che era entrato, scendeva giù e andava a sbattere contro la parete di fronte e illuminava il muro dal punto D, a metà, fino giù in basso al punto A.
Quando gli archeologi hanno disegnato la figura hanno scritto che le pareti CB e AB della piramide sono entrambe inclinate di 80°, che il punto D si vede, dal punto C a piano terra, con un angolo di 60°, che il punto E si vede , guardandolo dal punto A, sempre a piano terra, con un angolo di 70°.
Però nessuno ha avuto il coraggio di arrampicarsi per misurare l'angolo che forma il fascio di luce che entra nel punto E.
Insomma, questo angolo AED è irreperibile, come dicono loro è una incognita.
Io, parlando con il Vinicio Barbareschi, che è il Presidente, gli ho chiesto: “ Ma perché vi interessa questo angolo, che cosa ha di speciale?” Lui mi ha risposto “Questa è la Scienza, Pautasso, bisogna capire tutto, sapere tutto, senza preoccuparsi se serve o non serve!”
Allora, quando sono andato a casa, volendo essere di aiuto alla Scienza, oltre a fare fotocopie e scannamenti, ho chiamato il mio nipotino che fa la quinta e gli ho detto “Oreste (si chiama Oreste come me), hai mica quel disco con tutti i numeri... sì, il goniometro?” Lui lo ha preso da dentro la cartella e me lo ha dato. La mattina dopo sono andato dal Presidente e gli ho mostrato il goniometro. “Possiamo misurare l'angolo con questo” gli ho detto. “No, Pautasso, dobbiamo fare una cosa scientifica, così sono buoni tutti...”
Allora ho pensato: “Beh, io glielo chiedo ai Maghi, vuoi che non salti fuori qualche buona idea?”
Cari Maghi, se decidete di fare un quiz per i lettori su questo dilemma, mi raccomando di spiegargli, con i dovuti modi, che è proibito usare il goniometro.
Vi saluto con grande dedizione.
Oreste Pautasso"
Si tratta, quindi, con riferimento alla figura riportata sopra, di calcolare il valore dell'angolo AED.
SUGGERIMENTO del 27/2/2017: Solo una precisazione: il quiz può essere affrontato, oltre che per via analitica, anche per via grafica. Non è propriamente una via direttissima... ma alla fine basta la geometria delle scuole medie. Magari ne trovate una voi ancora più diretta.
La soluzione sarà pubblicata entro la prima settimana di marzo. Eccola!
QUI trovate tutti i quiz del Club dei Maghi e QUI tutti i quiz pubblicati sul blog






7 commenti
Non semplicissimo, vero ? Eh si, ci diamo da fare per proporre quiz adatti ai lettori del Circolo e poi Oreste se ne esce fuori sempre con dei problemi astrusi...
Solo una precisazione: il quiz può essere affrontato, oltre che per via analitica, anche per via grafica. Non è propriamente una via direttissima... ma alla fine basta la geometria delle scuole medie. Ma magari ne trovate una voi ancora più diretta.
Devo dire che ho faticato parecchio per provare a risolvere questo quiz ... e poi sicuramente ci sono sistemi più semplici.
... e poi sicuramente ci sono sistemi più semplici.
Parto dalla figura iniziale... che rappresento usando degli assi cartesiani....
Come si vede del triangolo Rosso si conosce solo un angolo, che misura 110° (180°-70°), dato che la retta AE quando interseca la parallela dell'asse X forma un angolo di 70° e quindi l'angolo del triangolo rosso vale 110° (quello che manca a 70° per formare un angolo piatto, ossia di 180°).
Basta ricavare l'angolo α per trovare immediatamente quello misterioso, ossia β, dato che la somma degli angoli di un triangolo (quello rosso) deve essere uguale a 180°, quindi:
β + α +110° = 180°
β = 180°- 110°- α
β = 70° - α
Per ricavare l'angolo α, ho deciso di usare il coefficiente angolare delle varie rette m, dato che questo rapporto per una retta rimane costante:
m = y/x = Tan angolo della retta
Pertanto considerando i vari segmenti e gli angoli conosciuti, ottengo:
Tan 80° = Dy/Dx = By/Bx = Ey/(Cx-Ex)
Tan 70° = Ey/Ex
Tan 60° = Dy/(Cx – Dx)
Tan α = (Ey -Dy)/(Ex-Dx)
A questo punto, provo a ricavare le coordinate di Ey; Dy; Ex; Dx.
Parto dalla relazione:
Ey = Tan 80°Cx - Tan 80°Ex
ma By/Bx = Tan 80°
Bx = By/Tan 80° …. ma Cx = 2Bx
Ey = Tan 80°2By/Tan 80° - Tan 80°Ex = 2By - Tan 80°Ex
ma Ey = Ex Tan 70°
Ex Tan 70°= 2By - Tan 80°Ex
Ex (Tan 70° + Tan 80°) = 2By
Ex = 2By/(Tan 70° + Tan 80°)
Poi passo alla relazione:
Dy = Tan 60°Cx - Tan 60°Dx
ma Cx = 2Bx = 2By/Tan 80°
Dy = 2By Tan 60°/Tan 80°- Tan 60°Dx
ma Dy = Tan 80° Dx
Tan 80° Dx = 2By Tan 60°/Tan 80°- Tan 60°Dx
Dx (Tan 80°+ Tan 60°) = 2By Tan 60°/Tan 80°
Dx = 2By Tan 60°/Tan 80°(Tan 80°+ Tan 60°)
Poi ricavo Ey:
Ey = 2By - Tan 80°Ex
Ex= Ey/Tan 70°
Ey = 2By - Ey Tan 80°/Tan 70°
Ey + Ey Tan 80°/Tan 70° = 2By
(EyTan 70° + Ey Tan 80°)/Tan 70° = 2By
Ey (Tan 70°+ Tan 80°) = 2By Tan 70°
Ey= 2By Tan 70°/(Tan 70°+Tan 80°)
Infine trovo Dy:
Dy = 2By Tan 60°/Tan 80°- Tan 60°Dx
Dx= Dy/Tan 80°
Dy = 2By Tan 60°/Tan 80°- Dy Tan 60°/Tan 80°
Dy + Dy Tan 60°/Tan 80° = 2By Tan 60°/Tan 80°
(Dy Tan 80°+ Dy Tan 60°)/Tan 80° = 2By Tan 60°/Tan 80°
Dy (Tan 80°+ Tan 60°) = 2By Tan 60°
Dy = 2By Tan 60°/(Tan 80°+ Tan 60°)
A questo punto non resta che ricavare i due segmenti (Ey-Dy e Ex-Dx) il cui rapporto è uguale alla tangente dell'angolo α:
Ey-Dy =2By Tan 70°/(Tan 70°+Tan 80°) -2By Tan 60°/(Tan 80°+ Tan 60°)
Ey-Dy=2By Tan 70°(Tan 80°+ Tan 60°) -2By Tan 60°(Tan 70°+Tan 80°)/(Tan 80°+ Tan 60°)(Tan 70°+Tan 80°)
Ey-Dy = 2By (Tan 70°Tan 80°+ Tan 70°Tan 60° -Tan 60°Tan 70°-Tan 60°Tan 80°)/(Tan 80°+ Tan 60°)(Tan 70°+Tan 80°)
Ey-Dy=2By (Tan 70°Tan 80°- Tan 60°Tan 80°)/(Tan 80°+ Tan 60°)(Tan 70°+Tan 80°)
Ex-Dx= 2By/(Tan 70° + Tan 80°)- 2By Tan 60°/Tan 80°(Tan 80°+ Tan 60°)
Ex-Dx= 2By Tan 80°(Tan 80°+ Tan 60°) -2By Tan 60°(Tan 70° + Tan 80°)/Tan 80°(Tan 80°+ Tan 60°)(Tan 70° + Tan 80°)
Ex-Dx= 2By(Tan 80°Tan 80°+ Tan 80°Tan 60°- Tan 60°Tan 70° - Tan 60°Tan 80°)/Tan 80°(Tan 80°+ Tan 60°)(Tan 70° + Tan 80°)
Ex-Dx= 2By(Tan 80°Tan 80°- Tan 60°Tan 70°)/Tan 80°(Tan 80°+ Tan 60°)(Tan 70° + Tan 80°)
Non resta che trovare il rapporto:
Tan α = (Ey-Dy)/(Ex-Dx)
Tan α = 2By (Tan 70°Tan 80°- Tan 60°Tan 80°)/(Tan 80°+ Tan 60°)(Tan 70°+Tan 80°) 2By(Tan 80°Tan 80°- Tan 60°Tan 70°)/Tan 80°(Tan 80°+ Tan 60°)(Tan 70° + Tan 80°)
Tan 80°(Tan 70°Tan 80°- Tan 60°Tan 80°)/(Tan² 80°- Tan 60°Tan 70°)
(Tan² 80°Tan 70°- Tan 60°Tan²80°)/(Tan² 80°- Tan 60°Tan 70°)
Tan² 80° (Tan 70°- Tan 60°)/(Tan² 80°- Tan 60°Tan 70°)
divido sopra e sotto per Tan² 80°
Tan α = (Tan 70°- Tan 60°)/(1- (Tan 60°Tan 70°/Tan² 80°)
per trovare l'angolo α , basta ricavare l'arcotangente:
α = arcoTan (Tan 70°- Tan 60°)/(1- (Tan 60°Tan 70°/Tan² 80°) = 50°
Ovviamente l'angolo misterioso è uguale a:
β = 70° - α = 70° -50° = 20°
Sicuramente c'è qualche metodo più veloce e semplice, ma meglio che far fotocopie....
Paolo
Provo con i teoremi sui triangoli qualunque.
Uso dei valori per confrontarli con quelli misurati con righello, considero AC=20
Lato AE=20 sen 70/sen 50=24,533631938113549316233036163762
Ribalto il triangolo:
Lato CE=20sen 60/sen 50=22,610317496942722139407175021118
Lato d=39,39231012048832237466972098358-22,610317496942722139407175021118=
16,781992623545600235262545962462
Lato e=30,641777724759121408095706022216-24,533631938113549316233036163762=
6,108145786645572091862669858454
Lato DE= f=13,6808(ho perso gli altri decimali)
Cosα=(f²+d²-e²)/2fd=0,93969267295227904834644367815345
Quindi α=19, 19,999991261001563303647820520439 quasi 20°
Gianfranco, potresti esplicitare a quali triangoli hai via via applicato il teorema dei seni e poi quello di Carnot ?
Provo con i teoremi sui triangoli qualunque.
Uso dei valori per confrontarli con quelli misurati con righello, considero AC=20
C° il punto di intersezione AE-CD
Lato CC°=20 sen 70/sen 50=24,533631938113549316233036163762
Ribalto il triangolo:
Lato AC°=20sen 60/sen 50=22,610317496942722139407175021118
Lato d=AE-AC°=39,39231012048832237466972098358-22,610317496942722139407175021118=
16,781992623545600235262545962462
Lato e=CD-CC°=30,641777724759121408095706022216-24,533631938113549316233036163762=
6,108145786645572091862669858454
Lato DE= f=13,68080573302674932176398458729 (recuperato da foglietto smarrito)
Cosα=(f²+d²-e²)/2fd=0,93969262078590838405410927732473
Quindi α=20°
Grazie Gianfranco.
Adesso è chiaro il calcolo dei lati "d" ed "e", ma non quello del lato "f", cioè DE, perché è visibile solo il risultato ma non la formula , né il ragionamento, da cui esso deriva. Puoi chiarire da dove viene fuori quel valore ?
scusate se mi intrometto... ma io suggerirei anche la soluzione geometrica, senza calcoli trigonometrici e con un po' di linee aggiuntive... in fondo sono solo triangoli simili
