Su Papalla sono un po' preoccupati che solo un terricolo ha risposto ad una delle tre domande del quiz... prima hanno pensato ad un problema di comunicazione... poi hanno pensato che i terricoli forse assomigliano agli abitanti del pianeta timido, meglio noti come i timidoni...

Nel dubbio,  per ricavare la magica figura capace di rispondere alle domande del quiz (qui), abbiamo chiesto aiuto a Papalpittore ed a PapalSempliciotto.

Per ricavare questo disegno, avverte Papalpittore, bisogna prima risolvere due piccoli problemi:

• come confrontare le dimensione dei dischi di stella e pianeti, visti da un pianeta qualsiasi;

• come rappresentare graficamente i raggi dei pianeti, dato che sono molto più piccoli (migliaia di chilometri) delle distanze in gioco (milioni di chilometri).

PapalSempliciotto ha già aiutato Papalpittore a disegnare ipotetici paesaggi visti dai pianeti trappisti (qui) ed in quel frangente era già emerso che il diametro apparente del disco dipende sia dalla dimensione reale del suo raggio, sia dalla sua distanza dall'osservatore.

Il rapporto raggio/distanza, indica quanto appare grande il disco.

PapalSemplicotto, chiede a Papalpittore, ma come si possono confrontare le dimensioni di due dischi?

Semplice, risponde PapalPittore, se tu hai un asta lunga 1 metro e vuoi sapere quante volte è più piccola o più grande rispetto ad una seconda asta, basta eseguire il rapporto tra queste due lunghezze:

confronto tra lunghezze : (Lunghezza asta 1)/(Lunghezza asta 2)

Per esempio se la seconda asta è lunga 2 metri:

confronto tra lunghezze : 1 metro/2 metri = ½ ossia la prima asta è lunga la metà della seconda.

Se, invece la seconda asta è lunga 0,5 metri:

confronto tra lunghezze: 1 metro/0,5 metri = 2 ossia la prima asta è  il doppio della seconda.

PapalSempliciotto, dopo questa piccola premessa, viene invitato da Papalpittore a confrontare i dischi apparenti di due sfere.

La sfera verde di raggio 1 mt è posta ad una distanza di 16 mt e quella rossa di raggio 2 mt è posta alla distanza doppia di 32 mt.

Ovviamente, questa configurazione in cui le due sfere appaiono uguali è solo una tra le tante possibili...

Il disco della sfera verde potrebbe apparire più grande di quello della sfera rossa, o viceversa, ma in ogni caso il rapporto tra raggi e distanze continua a indicare quante volte un disco (o meglio il suo raggio ed il suo diametro) appare più grande o più piccolo dell'altro.

rapporto tra dischi apparenti = r1 d2/r2 d1

Ora PapalSempliciotto è pronto per confrontare i dischi apparenti delle sfere, mutando la loro configurazione...

PapalSemplicotto, non solo ha mostrato come confrontare le proporzioni apparenti delle due sfere (o meglio dei loro raggi e diametri apparenti), mostrando diverse configurazioni e diverse relative possibili eclissi, ma ha anche risolto il secondo problema, poiché aumentando la dimensione di tutti i raggi della stessa proporzione, il rapporto apparente tra dischi non cambia!

D'altronde come potrebbe cambiare questo rapporto moltiplicando entrambi i raggi per 100?

rapporto tra dischi apparenti = 100 r1 d2/100 r2 d1 = r1 d2/r2 d1

Papalpittore è soddisfatto, poiché ora ci sono tutti gli ingredienti per realizzare la magica figura.

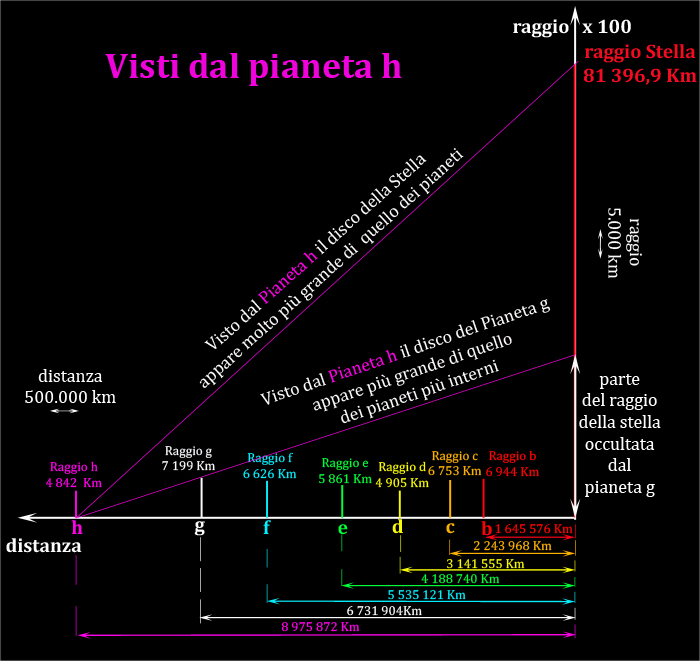
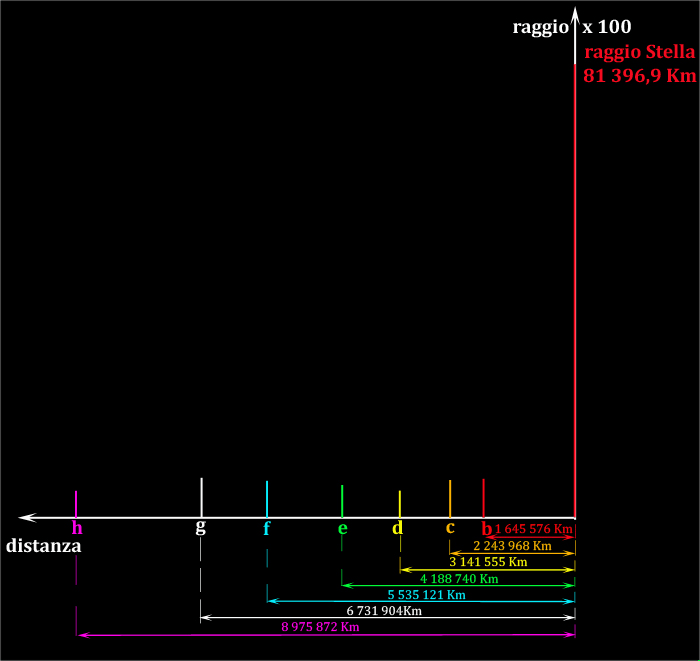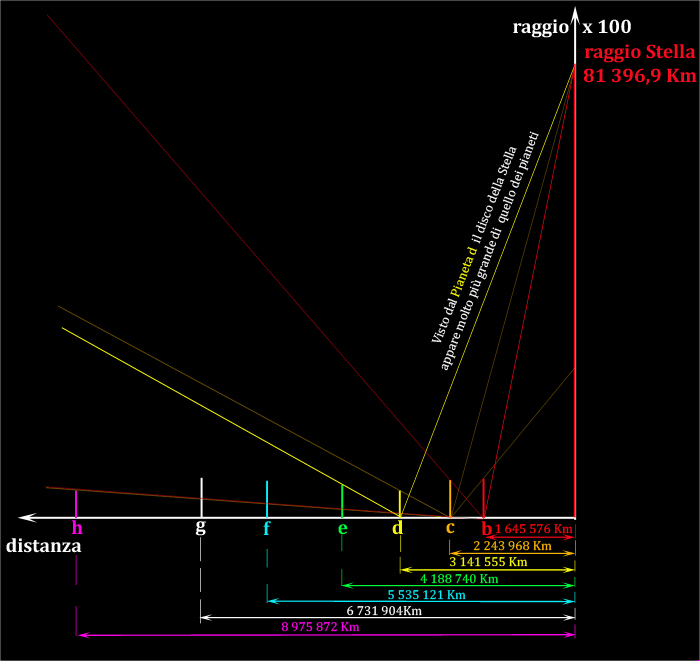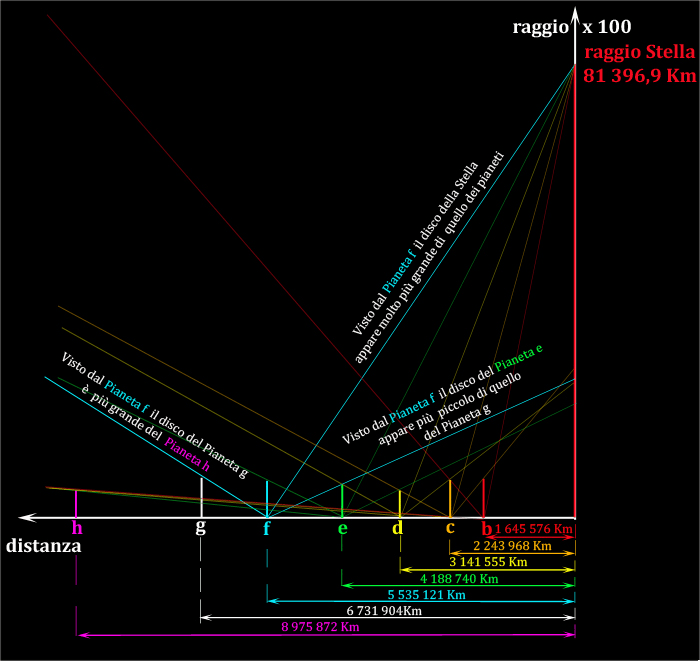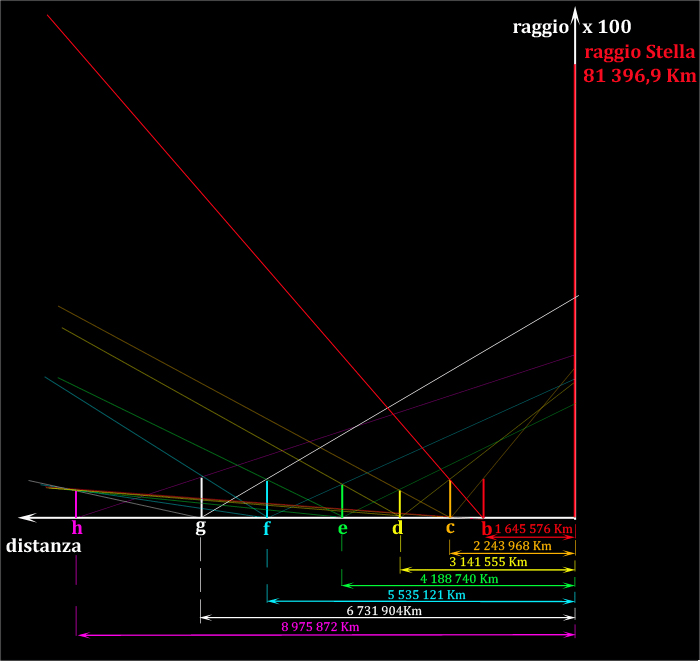
Sulle ascisse sono riportate le distanze dei pianeti dalla Stella, mentre sulle ordinate sono rappresentati i raggi di Stella e pianeti moltiplicati x 100.

La figura mostra cosa si vede dal pianeta più lontano (h).

Il segmento che congiunge il pianeta h al raggio della stella passa molto sopra ai raggi di tutti i pianeti, per cui il disco della Stella appare molto più grande di quello dei pianeti.

Il segmento che congiunge il pianeta h al raggio del pianeta g passa sopra ai raggi di tutti gli altri pianeti, per cui il disco del pianeta g è quello che appare più grande.

Prolungando questo segmento fino a raggiungere l'asse delle ordinate, è possibile verificare la porzione del raggio della stella occultata dal Pianeta g.

… è un po' come dire che se la stella fosse stata più piccola, tanto da far coincidere il suo raggio con la parte occultata dal pianeta g, entrambi i dischi visti dal pianeta h sarebbero apparsi di uguale dimensione...

Ora che la magica figura è stata trovata, non resta che rispondere alle domande poste dal Quiz.

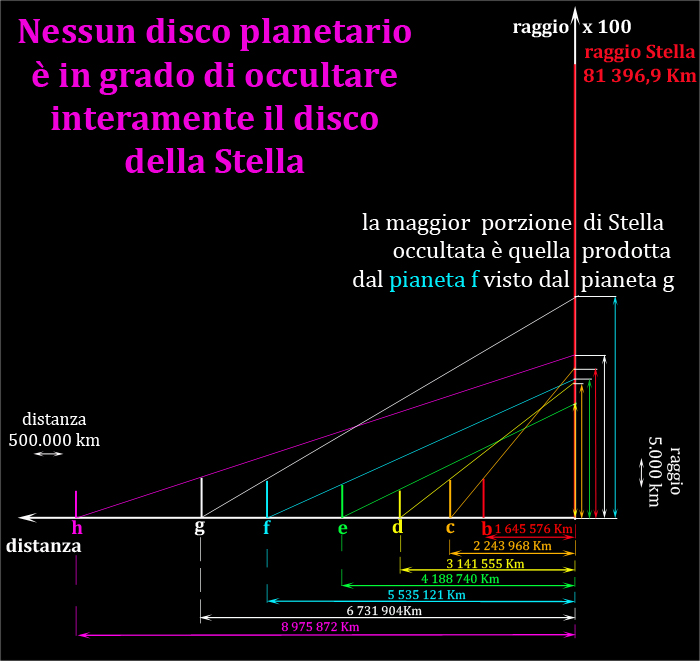
La figura mostra che nessun pianeta visto da un altro è in grado di occultare interamente la stella (ovviamente sono stati presi in considerazione solo i pianeti che appaiono più grandi).

L'occultazione della maggior porzione di stella è quella prodotta dal pianeta f visto dal pianeta g.

Papalpittore è soddisfatto poiché sono bastate poche righe tracciate sulla magica figura per rispondere alle prime due domande del quiz, in una sola volta.

Prima di disegnare la prossima figura, Papalpittore ci tiene a precisare che cambiando la scala dei raggi ciò che non cambia sono le proporzioni apparenti tra i vari dischi, ma se si vuole conoscere il diametro angolare della Stella o dei Pianeti occorre applicare la solita formuletta, ricavata qui:

diametro angolare apparente = 2 Arctan (raggio/distanza)

Ovviamente la distanza è quella dal pianeta di osservazione ed il raggio è quello della Stella oppure del pianeta di cui si vuole conoscere il diametro apparente.

Papalpittore, usando sempre la solita figura, mostra anche una particolare configurazione..

Questo è proprio uno dei casi posti dal quiz, ossia quando un pianeta occulta perfettamente l'altro, come nell'eclissi totale di Sole da parte della Luna (stesso diametro apparente dei due dischi).

Ma non è certo l'unico, per cui Papalpittore ha deciso di mostrare le varie fasi di costruzione della magica figura e le diverse configurazioni possibili con i pianeti interni..

e non contento anche di quelli esterni, visti dal lato oscuro dei vari pianeti, con l'aggiunta di qualche interessante confronto...

Papalpittore non può che far notare che in fin dei conti sono bastati pochi simpatici  numeri, quelli relativi a distanze e raggi, per costruire una semplice figura e con poche righe si è arrivati a rispondere alle domande del quiz....

Ora non resta che aggiungere un pizzico di fantasia...

Ah... dimenticavo... i papalli si sono premurati di avvisare che se ci sono domande o se c'è qualcosa che non è chiaro di non rimanere silenti come nel pianeta delle bocche cucite, ma di dirlo apertamente e senza timore.... nessuno deve rimanere escluso dai giochi papalliani...