Per parlare della determinazione della distanza del Sole non possiamo assolutamente non richiamare il contributo dei grandi scienziati greci. Non sono cose nuove e le abbiamo già trattate (per esempio QUI e QUI), ma è giusto tornarci brevemente sopra per dare un quadro storico-scientifico il più completo possibile.

La determinazione della distanza del Sole acquista un valore che va ben al di là del suo valore astronomico. Lontananza vuole anche dire dimensioni tali da introdurre scale di grandezze decisamente diverse da quelle in cui l’uomo appena nato era abituato a muoversi. Ancora oggi la gente si spaventa delle distanze cosmiche e tende quasi ad annullarle dalla propria mente terrena, quasi fossero favole. A maggior ragione, erano impensabili molto secoli fa, quando tutto doveva essere circoscritto alla realtà quotidiana, perfino la casa degli dei. Tutto doveva essere a portata di mano o di … dromedario o poco più.

Qualsiasi fosse il sistema prescelto (geocentrico o eliocentrico) l’azzardo di voler calcolare distanze extra terrene in modo matematico e geometrico implicava un’apertura mentale e una volontà di conoscere che ben raramente si trova ai nostri giorni.

La questione era semplice nella sua enormità: trovare una grandezza assoluta che potesse descrivere l’Universo conosciuto, almeno per quanto riguardava i pianeti (tra cui il Sole). Prima ancora di conoscere il proprio pianeta si voleva collocarlo in uno spazio ben più completo. E già l’idea di “spazio” dovrebbe lasciare a bocca aperta.

Ovviamente, fino a che il Sole era uno dei tanti sudditi della Terra, la sua distanza non aveva niente di speciale e poteva valere quella della Luna o di qualsiasi altro pianeta. Con l’avvento della teoria eliocentrica (QUI la vera storia della rivoluzione copernicana, così come l'ha immaginata Giacomo Leopardi , tradotta da Vin-Census), invece, questa distanza divenne fondamentale e lo fu ancora di più con la stesura delle leggi di Keplero. La terza diceva in pratica che bastava conoscere una sola distanza tra la Terra e un pianeta (quanto meno nelle configurazioni giuste) per ricavare tutte le altre, compresa quella del Sole. Le dimensioni del Sole, la sua difficile osservazione diretta e l’impossibilità di avere sia lui che i pianeti contemporaneamente visibili, ha presto fatto capire che si poteva arrivare a questa distanza fondamentale solo in modo indiretto.

Quanto detto risulta abbastanza ovvio da un punto di vista storico. Da Tolomeo (meglio ancora da Ipparco) fino a Keplero la distanza del Sole è rimasta estremamente aleatoria e niente si è aggiunto a quanto trovato dai sommi greci precedenti. In realtà, nemmeno Keplero e i suoi contemporanei sono riusciti a far molto di più e si è dovuti arrivare alla fine del 1600 per iniziare una campagna di tipo teorico e osservativo mirata allo scopo.

I secoli bui del geocentrismo si sono riflessi pari pari sulla distanza del Sole, nell’ambito di una visione del Cosmo di tipo religioso e non scientifico. Poco importava, in fondo, dove si trovasse realmente la fonte della luce e del calore (la vita stessa dell’uomo), ma era molto più importante attribuire il tutto a una scelta divina. In poche parole, il Sole era una “lampadina” offertaci da Dio, come la Luna ne era un’altra a “basso costo”. L’importante è che facessero il loro lavoro preordinato da un Essere Superiore.

Tuttavia, il genio di Aristarco, Ipparco ed Eratostene aveva lasciato il segno e certi risultati non potevano essere trascurati del tutto, quasi fossero stati una piccola informazione regalataci dal Supremo. E così si spiega perfettamente quanto si vede nella Fig. 1 (dell’articolo precedente), con quel vuoto triste e indicativo tra le due misure uguali di prima del Mille e del 1600. Secoli di buio, mentre il Sole continuava a regalarci la luce e la vita…

Molti secoli possono tranquillamente essere cancellati nella storia dell’Astronomia e si potrebbe incollare Tolomeo a Copernico, senza accorgersi della nullità che contiene il tempo trascorso.

Torniamo, quindi, ad Aristarco, un nostro amico carissimo e una delle più grandi menti nella storia dell’uomo. Egli compie un primo passo fondamentale, non spaventandosi affatto del fenomeno delle eclissi, ma utilizzandolo per la determinazione della prima distanza cosmica: la distanza tra la Terra e la Luna. E lo fa ottenendo un successo enorme sia in termini di valore numerico, sia in termini di accettazione quasi ovvia (ma proviamo a metterci nei panni di quegli uomini che vedevano e pensavano soltanto con i mezzi naturali a disposizione e poco più… noi oggi balbetteremmo con gli occhi sbarrati se ci portassero via PC, cellulari e… Celestia) di distanze al di fuori completamente di quelle misurabili dai dromedari o dalle barche chiamate navi. Già questa accettazione è un risultato incredibile della mente umana.

Ma veniamo a noi… Aristarco segue con molta attenzione il fenomeno dell’eclissi di Luna. Si accorge che essa capita quando la Luna entra all’interno dell’ombra della Terra. Pensiamo a quante intuizioni meravigliose sono già inserite in queste semplici constatazioni. Il Sole è l’origine della luce e la Terra può bloccarla, producendo un cono d’ombra che si proietta nello spazio ed ha forma circolare. Notiamo subito il concetto di tridimensionalità a grande scala e la sfericità dei corpi celesti, assunta come dato di fatto del tutto normale.

Subito dopo vi è bisogno di passare a misure vere e proprie per applicare una matematica semplice, ma efficacissima. E allora, perché non considerare il Sole a una distanza enormemente grande (già questa è un’intuizione di portata fantastica), in modo che il cono d’ombra si trasformi in un cilindro? Infatti, se il Sole fosse relativamente vicino, l'ombra creata dalla Terra avrebbe forma conica, quindi un diametro maggiore di quello terrestre. Ricordiamoci che la trigonometria non è ancora nata e vi è un approccio empirico alle relazioni tra archi e angoli. Il fatto stesso, però, che venga applicata questa semplificazione (del tutto giustificabile) la dice lunga sulla solidità dei concetti che governano la mente di Aristarco.

A questo punto può eseguire il suo gioco geometrico, che forse non tanti studenti di oggi sarebbero in grado di pensare ed eseguire.

Immergiamoci nella Fig. 2.

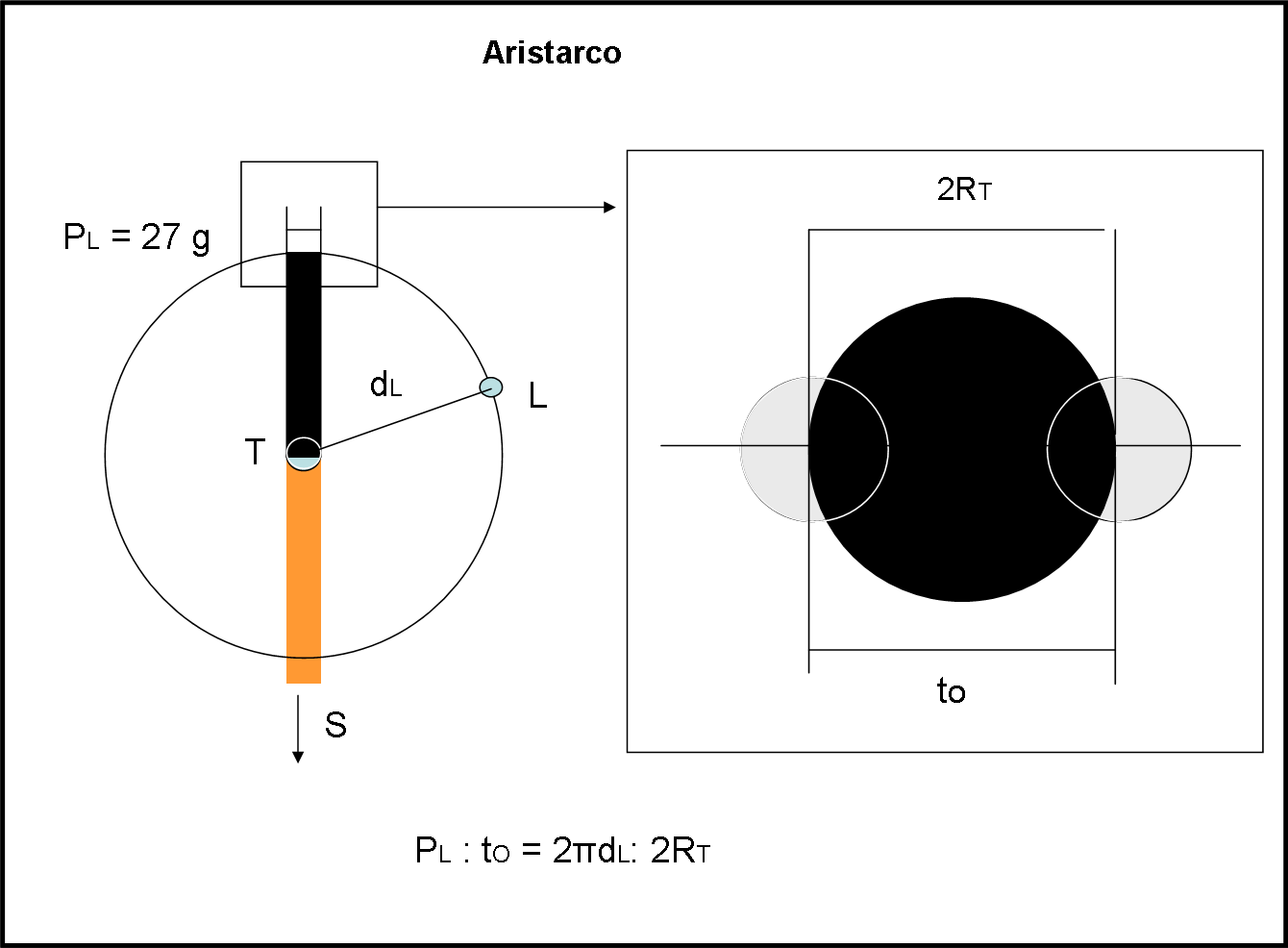
Incominciamo con la parte destra, quella maggiormente “osservativa”. Il cerchio nero è l’ombra della Terra che ha come diametro proprio il diametro della Terra, dato che il cono d’ombra è stato assunto uguale a un cilindro. La Luna è più piccola dell’ombra (e quindi della Terra… già queste riflessioni sono geniali per quei tempi) e impiega un certo tempo ad attraversare il cerchio dell’ombra.

In poche parole, Aristarco riesce a misurare il tempo t_O relativo all’ingresso del punto centrale della Luna (piena e quindi facilmente misurabile) e la sua uscita. Questo tempo corrisponde esattamente al diametro del nostro pianeta. Scusate se mi ripeto, ma queste semplici operazioni comportano una mente capace di riflettere, di decidere e di convincersi di essere nel giusto… e siamo a più di due secoli dalla nascita di Cristo. Tuttavia, non stupiamoci più di tanto, pensando di quali sculture e di quali costruzioni si riempivano le città… I greci adoravano gli dei e se ne sentivano schiavi, ma in loro onore estraevano il meglio dal loro cervello (qualcosa di molto simile al nostro Rinascimento artistico, da cui proprio il nome).

Non ci resta, adesso, che passare alla parte di sinistra della figura, dove il tutto è visto dall’alto. Anch’essa è un miracolo di intuizione e di capacità di estrapolazione priva di alcun timore mistico. La Luna gira intorno alla Terra e Aristarco sa benissimo quanto tempo ci impiega! Circa 27 giorni. Ora non resta che mettere in piedi una semplice proporzione.

Il periodo completo della rivoluzione della Luna attorno alla Terra sta al periodo necessario al centro della Luna per entrare e uscire dal cerchio d’ombra come la circonferenza completa della traiettoria circolare della Luna sta alla lunghezza dell’ombra terrestre. In formule…

P_L : t₀ = 2πd_L : 2R_T

P_L e t₀ sono noti per cui si può facilmente ricavare la distanza della Luna in funzione del raggio terrestre R_T

Aristarco si ferma qui, dato che il raggio della Terra è ancora sconosciuto (ma per poco!).

Il suo risultato porta a un valore pari a:

d_L ≈ 60 R_T

Utilizzando il raggio medio conosciuto oggi (6373 km), si ottiene una distanza lunare pari a:

d_L = 382 000 km

Mi vergogno quasi a dire che il semiasse misurato oggi è pari a 384 000 km.

Fortuna o genio? Io so già la risposta, ma lascio a voi la scelta…

Qualcuno potrebbe dirmi: “Sì, oggi sappiamo che è giusto, ma Aristarco doveva accontentarsi di mettere 30 terre in fila…”. No, dato che probabilmente non solo ha saputo ma, magari, ha anche incontrato il suo collega Eratostene (immaginiamoci un loro discorso… ho quasi la pelle d’oca a questo pensiero). Lui ha appena calcolato la circonferenza della Terra con  il suo meraviglioso dromedario e può dargli il valore del raggio della Terra (ammettiamo in chilometri). Esso risulta:

R_T = 6314 km

Da cui…

d_L = 379 000 km

Un po’ meno preciso? Sì, sicuramente, ma soffermiamoci ancora una volta a pensare che quei due personaggi stavano parlando di distanze del tutto estranee alla realtà in cui vivevano, eppure non ne erano affatto sconvolti. Di fronte a terre piatte e a cento altre illazioni, loro avevano impostato dei solidi e gli avevano regalato uno spazio ben definito. Non ci ricorda lo spazio conquistato dall’uomo masaccesco del Rinascimento o i teatri prospettici perfetti di Piero della Francesca ?

Quante cose potrebbero essere insegnate nelle scuole attraverso lo studio degli antichi, anche dal punto di vista psicologico ed etico!

Dalla Luna al Sole il passo è breve… basta conoscere bene le fasi lunari e la loro causa (altra scoperta che ha del meraviglioso). Non resta che disegnare un triangolo rettangolo, con l’angolo retto nella Luna. La Fig. 3 (già da tutti noi ben conosciuta) è fantastica: è sufficiente misurare l’angolo tra il Sole e la Luna quando essa è in quadratura (ossia se ne vede la metà) e il gioco è fatto!

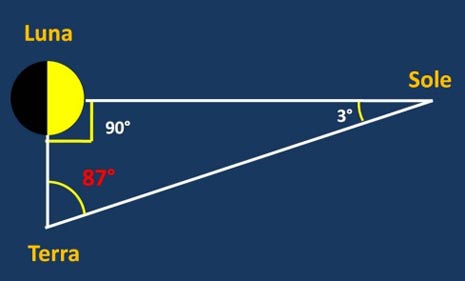
Purtroppo. misurare un angolo così vicino a 90° non è cosa semplice o  -meglio- un piccolo errore influisce enormemente sulla misura finale. Aristarco ricava 87°, quasi giusto, ma…

Oggi, possiamo capire questo enorme problema considerando il rapporto tra distanza Luna-Sole (più o meno uguale a quella Terra-Sole) e la distanza Luna-Sole (ben conosciuta). Questo rapporto è la tangente trigonometrica di 87°. Ci ricordiamo molto bene come varia la tangente di un angolo… Un errore di 2.85 gradi per un angolo medio comporterebbe un errore sulla tangente trascurabile… Proviamo con 45°.

tan 45 = 1

tan 47.85 = 1.1

Proviamo, invece, a fare lo stesso vicino a 90°

tan 87 = 19

tan 89.85 = 381

i numeri stanno scappando verso l’alto, come d’altra parte sappiamo bene:

tan 90 =  ∞

Insomma, un errore più che “obbligatorio” per la strumentazione di quei tempi (ma il procedimento era perfetto) che ha comportato un “misero” fattore 19 tra la distanza del Sole e quella lunare. Oggi sappiamo che l’angolo vero era solo di 2.85 gradi più grande, sufficiente a ottenere un rapporto di 381.

Un risultato per la distanza solare del tutto assurda per noi, ma sarebbe bastato prestare, per pochi minuti, ad Aristarco un nostro strumento per misurare gli angoli (avrebbero imparato subito a usarlo) e avremmo già avuto una distanza quasi perfetta ai tempi di Aristarco e del suo degno compare Eratostene. Riflettiamo un attimo. Aristarco ed Eratostene non credono assolutamente al risultato che hanno ottenuto, “sanno” che il Sole DEVE essere molto più lontano, ma, al momento non possono fare di più. Sembra, infatti, che Aristarco abbia detto chiaramente che il valore 19 tra distanza del Sole e quello della Luna si doveva considerare come distanza minima. Lo stesso Eratostene considera senza problemi i raggi del Sole paralleli e lo stesso Aristarco considera l’ombra terrestre un cilindro. Approssimazioni che solo un Sole molto più lontano poteva permettere. Non un vero errore, quindi, ma la presa d’atto di una limitazione strumentale (così come per le parallassi stellari). Nei secoli bui, invece, venne considerato un valore definito, per quello che poteva interessare in uno spazio che tornava a essere praticamente piatto…

Mettiamo pure nel grafico di Fig. 1 (QUI) un valore pari a poco più di 7 milioni di chilometri (un numero che, comunque, doveva già incutere spavento), corrispondente a 0.048 UA circa. Come vedere, lo stesso valore arriva fino al 1600...

Non è stato da meno Ipparco, famoso per la determinazione quasi inconcepibile della precessione degli equinozi e per il suo catalogo stellare. Egli riprende molto di ciò che era stato eseguito da Aristarco (spesso si confondono le determinazioni di uno e dell’altro), ma ci regala un metodo diverso e più “matematico” per la determinazione della distanza Terra-Luna, fondamentale per arrivare (anche se con la stessa inesattezza pratica) alla distanza del Sole.

Ipparco sfrutta un’eclisse totale di Sole e la Fig. 4 ne illustra i punti salienti.

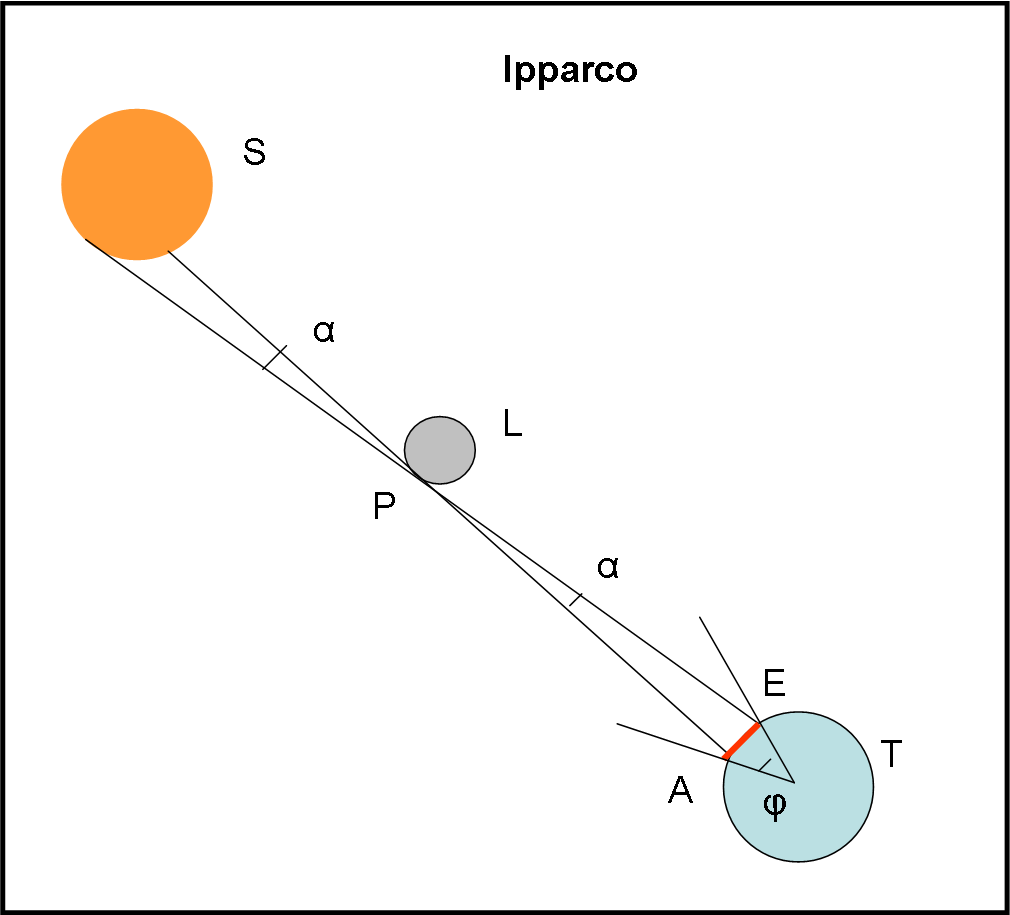
Il punto chiave di tutta la determinazione è la totalità vista dall’Ellesponto e la parzialità vista da Alessandria d’Egitto. In modo piuttosto accurato Ipparco riesce a determinare a che punto del Sole arrivava il bordo scuro della Luna vista da Alessandria, mentre vi è la totalità (tangenza) nell’Ellesponfo. In  poche parole, determina l’angolo parallattico α, che corrisponde all’angolo tra Alessandria e  l’Ellesponto visto dal bordo lunare. A questo punto basta conoscere la vera distanza tra A ed E e il gioco è fatto. Tuttavia, non è stato trovato (probabilmente) il dromedario adatto che avrebbe dovuto camminare sul mare per andare il linea retta. Poco male… Ipparco conosce bene le posizioni delle stelle e in base a queste riusce a calcolare l’angolo φ al centro della Terra tra A ed E. Ormai Eratostene aveva ricavato il raggio terrestre e, quindi, Ipparco ricava la distanza tra A ed E, anche senza dromedario. Il suo risultato concordava quasi perfettamente con quello ottenuto da Aristarco e di conseguenza anche la distanza del Sole rimane pressoché invariata.

A questo punto, poco o niente cambiò e Tolomeo accettò di buon grado i risultati dei suoi predecessori e nulla mutò fino all’avvento della teoria copernicana e alle leggi di Keplero, ma soprattutto fino a una intuizione del tutto arbitraria, rivelatasi vera.

 

QUI la serie completa degli articoli dedicata alla storia del calcolo della distanza del Sole