Categorie: Fisica classica
Tags: ciliegia Pappo Peppa Pippo quiz rotazione sistema di riferimento soluzione
Scritto da: Vincenzo Zappalà
Commenti:3
Soluzione elementare del quiz della ciliegia *
Le risposte al quiz della ciliegia avute finora sono sicuramente “abbastanza” (a parte qualche incertezza sulle altezze) precise, ma sono anche un po’ troppo “elevate”. Bastava qualcosa di molto più empirico, ma sufficiente a Peppa per disegnare con buona precisione ciò che viene richiesto da Pappo e Pippo
Peppa non ha ancora molte nozioni di matematica e geometria, ma si accorge di poter fare uno schizzo abbastanza buono senza bisogno di fare considerazioni troppo elevate per lei. Si affida, perciò, all’unica cosa di cui è sicura: la traiettoria vista dal riferimento esterno (Pippo), così come quella vista da Pappo con la piattaforma ferma, deve essere una parabola. E quella la sa disegnare (conoscendo l’accelerazione di gravità g e sapendo come scomporre il vettore velocità)!
Il problema rimane quello di disegnare la traiettoria nel sistema di riferimento rotante. Ovviamente, per il sistema di Pippo, nulla cambia: la ciliegia percorre la stessa traiettoria parabolica precedente. C’è anche da dire che questa curva rimane sempre valida e ciò che cambia e l’apparenza che essa viene ad avere nel sistema rotante. Il fenomeno fisico deve, comunque, essere lo stesso: la ciliegia parte da Pippo e arriva in bocca a Pappo.
La parabola, dovendo partire e arrivare alla stessa altezza deve avere il suo massimo in L/2 e dopo un tempo τ/2.
Tuttavia sappiamo, anche, che τ = 2T, dove T è il periodo che Pappo impiega a effettuare una rotazione.
Peppa disegna allora la traiettoria di Pippo rispetto a Pappo considerato FERMO. Essa non è altro che una circonferenza di raggio L (Fig. 1, in basso) ed è percorsa in senso orario con velocità angolare
ω = 2π/T
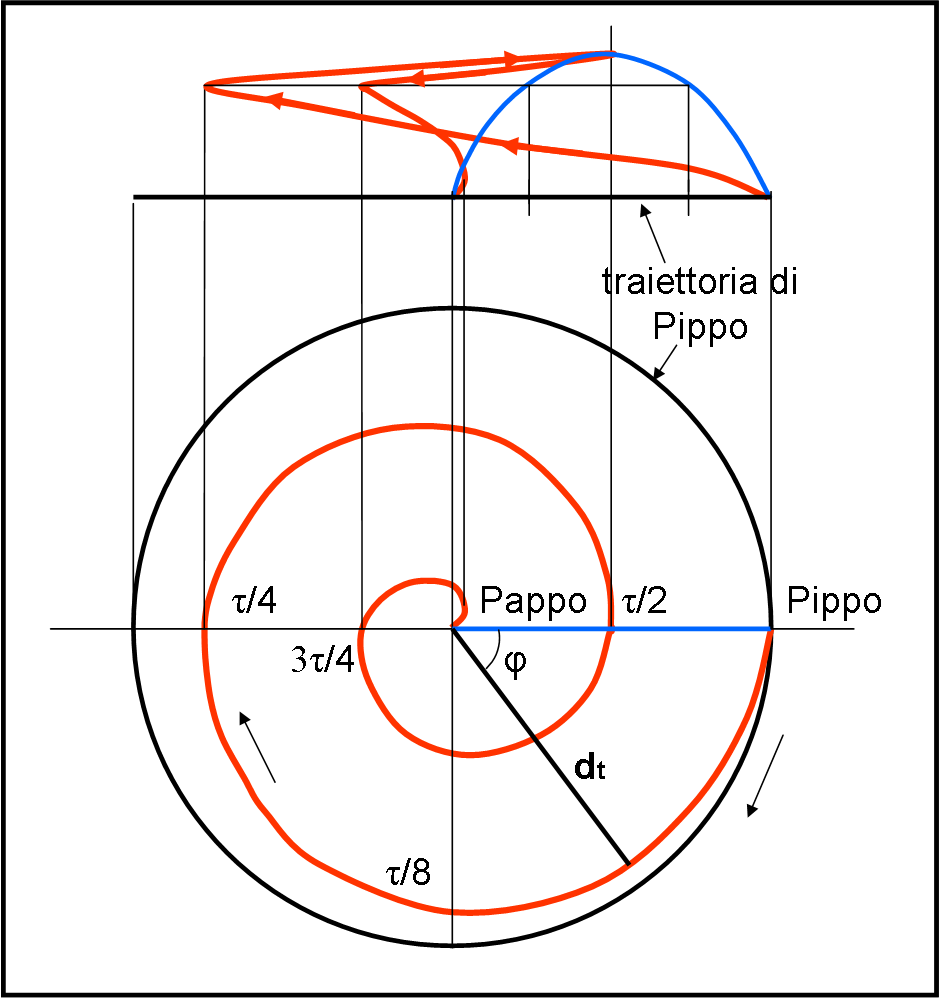
La rotazione angolare è costante, perciò vale anche la relazione (φ è l’angolo percorso da Pippo e anche dalla ciliegia che si muove SEMPRE nel piano perpendicolare alla congiungente Pappo-Pippo, ):
ω = φ/t
φ = ω t
φ = 2π t/T
φ = 4π t/τ …. (1) (dato che T = τ/2)
E perciò facilissimo ricavare l’angolo φ relativo al tempo desiderato
Ovviamente, per t = 0, φ = 0
Prendiamo qualche tempo particolare (ma potremmo calcolarne molti di più)
t = τ/8
φ = 4π t/τ = 4π τ/(8τ)
φ = π/2
Abbiamo l’angolo di posizione, ma ci manca la distanza della ciliegia da Pappo …
Tuttavia, se vogliamo disegnare ciò che avviene nel piano orizzontale (quello che contiene la piattaforma), sappiamo che il moto della ciliegia è un moto rettilineo uniforme. In poche parole, la componente della velocità lungo la direzione Pappo-Pippo è sempre la stessa per tutto il tempo τ. Chiamiamo questa velocità costante vr (ma ci importa poco il suo valore). Chiamiamo, anche, Lt
la distanza contata a partire da Pippo, dove t = 0.
vr = L/τ = Lt/t
Lt = t L/τ
Ma, ricordando la (1):
Lt = L (t/τ) = Lφ/4π
A noi interessa la distanza da Pappo (dt) che è uguale a:
dt = L - Lφ/4π = L (1 - φ/4π)
Per t = τ /8, ossia per φ = π/2
dτ/8 = L (1 – π/8π) = 7/8 L
Il primo punto da disegnare (t = τ/8), mettendo Pappo al centro, partendo dalla direzione Pappo-Pippo e andando in verso orario, si ha per φ = π/2 e d = 7/8 L.
Disegniamo, adesso dei punti ancora più interessanti, che ci serviranno anche per la seconda parte.
t = τ/4
φ = 4π t/τ = 4πτ/4τ = π
dτ/4 = L (1 - φ/4π) = L (1 - 1/4) = 3/4 L
t = τ/2
φ = 4π τ /2τ = 2 π
dτ/2 = L (1 - φ/4π) = L (1 - 1/2) = L/2
t = 3/4 τ
φ = 4π t/τ = (4π 3τ)/(4τ) = 3π
d3/4τ = L (1 - φ/4π) = L (1 - 3/4) = L/4
t = τ
φ = 4π t/τ = 4π
dτ = L (1 - φ/4π) = L (1 - 1) = 0
E via dicendo… Non è difficile tracciare la curva rossa della parte bassa della Fig. 1
Adesso, però dobbiamo disegnare quello che capita nel piano perpendicolare.
La massima altezza raggiunta sarà legata alla velocità iniziale (in particolare alla componente verticale), ma Peppa, che sa disegnare la parabola della traiettoria della ciliegia (questo l’abbiamo accettato fin dall’inizio), non ha bisogno di fare tanti calcoli. L’altezza massima raggiunta deve rimanere la stessa.
A che angolo corrisponde questa altezza massima? Beh… la parabola raggiunge il suo massimo nel punto di mezzo, ossia quando t = τ/2, che corrisponde a φ = 2π, ossia dopo un giro completo di Pappo. Ciò vuol dire che prima di questo istante la traiettoria deve salire e dopo deve scendere, cambiando di verso.
E’ importante allora vedere cosa capita negli istanti τ/4 e 3τ/4. Essi hanno la stessa altezza, che può essere ricavata direttamente dalla parabola di partenza (azzurra). In quei punti la ciliegia cambia rapidamente direzione. Alla fine (parte alta della Fig. 1) deve arrivare nella bocca di Pappo, come mostrato nello “schizzo” qualitativo di Peppa che è più che sufficiente per lasciare di stucco i suoi fratelli.
Tuttavia (sempre graficamente), Peppa può fare molto meglio e studiare la traiettoria nei dintorni dei punti di cambiamento di direzione e anche della parte finale. Basta che consideri angoli φ abbastanza vicini, i quali ovviamente corrispondono a tempi t e distanze dt facilmente ricavabili. Dato il tempo è immediato ricavare le altezze dal moto parabolico.
A questo punto i nostri “maghi” e colleghi possono anche divertirsi ad andare più a fondo in modo analitico (le altezze, ad esempio, derivano direttamente dall’equazione del moto parabolico), cosa che hanno già fatto, almeno in buona parte…
Il quiz lo trovate QUI






3 commenti
Procedimento per ricavare le equazioni parametriche della traiettoria della ciliegia nel sistema di riferimento di Pappo.
Pappo in rotazione attorno al proprio asse, se considerato fermo vede muoversi in vero opposto tutto ciò che gli sta intorno. Anche la ciliegia lanciata da Pippo, quindi, viene vista da Pappo muoversi di moto rotatorio combinato con quello parabolico dovuto al lancio da parte di Pippo. Se considero un sistema di assi cartesiani x, y, z (con asse z passante per Pappo) e guardo tutto il sistema dall'alto, cioè "in pianta", chiamo con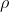 la distanza radiale (sul piano xy) tra la ciliegia e Pappo e con
la distanza radiale (sul piano xy) tra la ciliegia e Pappo e con  l'angolo tra l'asse x e la congiuntente (sul piano xy) tra Pappo e la ciliegia. Oriento inoltre la terna x, y, z in modo che l'asse x all'istante iniziale passi per la posizione di Pippo. In pratica queste sono le coordinate polari della ciliegia proiettata sul piano xy. Naturalmente , sia
l'angolo tra l'asse x e la congiuntente (sul piano xy) tra Pappo e la ciliegia. Oriento inoltre la terna x, y, z in modo che l'asse x all'istante iniziale passi per la posizione di Pippo. In pratica queste sono le coordinate polari della ciliegia proiettata sul piano xy. Naturalmente , sia 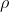 sia
sia  variano col tempo. In particolare,
variano col tempo. In particolare, 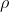 varia perché la ciliegia avanza verso Pappo, mentre
varia perché la ciliegia avanza verso Pappo, mentre  varia perché Pappo ruota intorno all'asse z. E' noto che il moto parabolico di un oggetto avente una data massa e velocità iniziale v inclinata di un certo angolo
varia perché Pappo ruota intorno all'asse z. E' noto che il moto parabolico di un oggetto avente una data massa e velocità iniziale v inclinata di un certo angolo  rispetto all'orizzontale, è dato dalla composizione di due moti, uno rettilineo uniforme nella direzione orizzontale e uno uniformemente accelerato nella direzione verticale. Poiché sto osservando il sistema "in pianta", per ora mi interessa solo il moto rettilineo uniforme in direzione orizzontale. La componente orizzontale della velocità è data da v cos
rispetto all'orizzontale, è dato dalla composizione di due moti, uno rettilineo uniforme nella direzione orizzontale e uno uniformemente accelerato nella direzione verticale. Poiché sto osservando il sistema "in pianta", per ora mi interessa solo il moto rettilineo uniforme in direzione orizzontale. La componente orizzontale della velocità è data da v cos  , avendo indicato con v il modulo della velocità iniziale di lancio della ciliegia. Se indico con L la distanza iniziale tra Pippo e Pappo, la ciliegia, a seguito del lancio, andrà avvicinandosi a Pappo e sul piano orizzontale, cioè il piano xy, la distanza tra Pappo e la ciliegia sarà data , istante per istante (istante iniziale t=0), dalla relazione (moto rettilineo uniforme) :
, avendo indicato con v il modulo della velocità iniziale di lancio della ciliegia. Se indico con L la distanza iniziale tra Pippo e Pappo, la ciliegia, a seguito del lancio, andrà avvicinandosi a Pappo e sul piano orizzontale, cioè il piano xy, la distanza tra Pappo e la ciliegia sarà data , istante per istante (istante iniziale t=0), dalla relazione (moto rettilineo uniforme) :
All'istante t, però, la ciliegia sarà ruotata attorno a Pappo di un angolo, in pianta, dato dalla relazione (moto rotatorio uniforme):
Da queste due relazioni, eliminando il parametro t, ricavo l'equazione della proiezione della traiettoria sul piano orizzontale, cioè:
Questa non è altro che l'equazione in coordinate polari di una spirale.
Al fine di ricavare le equazioni parametriche della traiettoria nello spazio, dalla (1) posso ricavarmi subito l'ascissa e l'ordinata (sul piano orizzontale xy) della ciliegia all'istante di tempo t:
dove) è dato dalla (3). In pratica , il parametro variabile è solo
è dato dalla (3). In pratica , il parametro variabile è solo ) , una volta fissati all'inizio del problema i valori di tutti gli altri (v,
, una volta fissati all'inizio del problema i valori di tutti gli altri (v, 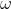 ,
,  , L. Dopo spiegherò che in realtà anche tra queste grandezze deve esistere una relazione)
, L. Dopo spiegherò che in realtà anche tra queste grandezze deve esistere una relazione)
Mi manca la coordinata z(t). A questo punto devo considerare la componente verticale del moto parabolico della ciliegia. Come noto, l'ordinata all'istante di tempo t di un punto materiale che venga lanciato in alto con velocità iniziale v ed angolo di inclinazione rispetto all'orizzontale pari ad è data da:
è data da:
Nel caso che interessa, però, al moto parabolico della ciliegia si somma quello di rotazione di Pappo. Per cui, all'istante di tempo t , la ciliegia sarà ruotata , in pianta, rispetto alla posizione iniziale, di un angolo che come già visto è dato dalla (2). Da questa mi ricavo t e sostituisco l'espressione nella (6), ottenendo in definitiva:
A questo punto ho le espressioni delle tre coordinate spaziali, la (4), la (5) e la (7), di un punto generico della traiettoria della ciliegia. In altre parole, ho ottenuto le equazioni parametriche di tale traiettoria spaziale, in cui il parametro variabile è) .
.
Inputando tali equazioni nel software geogebra ootengo il grafico della traiettoria , che a questo punto potrò guardare da qualsiasi direzione, sul piano xy, sul piano xz o quello yz, in assonometria o in prospettiva...
Dimenticavo di spiegare che tra le grandezze v,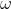 ,
,  , L deve esistere una relazione. Perché ? E' chiaro che L, per esempio , non può assumere qualsiasi valore. Infatti la ciliegia, lanciata da Pippo con velocità iniziale v ed angolo di lancio
, L deve esistere una relazione. Perché ? E' chiaro che L, per esempio , non può assumere qualsiasi valore. Infatti la ciliegia, lanciata da Pippo con velocità iniziale v ed angolo di lancio  , deve andare a finire, per dato del problema, nella bocca di Pappo. Quindi, in realtà, L, ossia distanza in pianta tra Pippo e Pappo dovrà coincidere con la "gittata", ossia con la distanza orizzontale coperta dalla ciliegia lanciata con quella velocità e con quell'angolo di lancio. Se, invece, considero L variabile come si vuole, allora dovrò dare a v o all'angolo di lancio yun valore tale che alla fine sia soddisfatta la condizione di base, cioè che la ciliegia finisca in bocca a Pappo. Anche la velocità di rotazione deve essere in relazione con le altre grandezze. In particolare, perchè la ciliegia finisca in bocca a Pappo esattamente dopo 2 giri di Pappo su sè stesso, si dimostra (tempo di volo della ciliegia deve essere uguale a quello impiegato da Pappo a fare 2 giri su sé stesso) che , se fissiamo la velocità iniziale e l'angolo di lancio, dovrà valere la relazione:
, deve andare a finire, per dato del problema, nella bocca di Pappo. Quindi, in realtà, L, ossia distanza in pianta tra Pippo e Pappo dovrà coincidere con la "gittata", ossia con la distanza orizzontale coperta dalla ciliegia lanciata con quella velocità e con quell'angolo di lancio. Se, invece, considero L variabile come si vuole, allora dovrò dare a v o all'angolo di lancio yun valore tale che alla fine sia soddisfatta la condizione di base, cioè che la ciliegia finisca in bocca a Pappo. Anche la velocità di rotazione deve essere in relazione con le altre grandezze. In particolare, perchè la ciliegia finisca in bocca a Pappo esattamente dopo 2 giri di Pappo su sè stesso, si dimostra (tempo di volo della ciliegia deve essere uguale a quello impiegato da Pappo a fare 2 giri su sé stesso) che , se fissiamo la velocità iniziale e l'angolo di lancio, dovrà valere la relazione:
In definitiva, le grandezze considerate, nel caso che interessa, sono tra loro dipendenti.
Ottimo Arturo!
Mettiti in contatto con gli altri maghi (compreso Paolo) e preparate un versione della soluzione NON elementare, con tanto di animazioni. E' meglio scrivere un articolo per averlo più facilmente a portata di mano...