Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.

 

Anche se con un po’ d’indifferenza, andiamo, comunque, avanti con le deformazioni subite da un oggetto che si muove con velocità relativistiche. Il primitivo righello si sta trasformando in qualcosa di più concreto e si prepara a regalarci effetti del tutto imprevisti.

In questo articolo diamo la soluzione del quiz precedente, spiegando molto qualitativamente cosa succede. Le domande erano tre e noi seguiremo proprio lo stesso ordine. C’è da dire che, malgrado il gran caldo, Arturo ha fornito una risposta più che valida e noi cercheremo solo di analizzarla meglio con qualche figura.

Iniziamo con la domanda più facile, relativa al righello verticale che si muove lungo una direzione parallela all’asse delle x. Vediamo subito la Fig. 1, che lo rappresenta. L’asse x è l’asse ottico AO della macchina fotografica M, mentre il righello si muove lungo CC’. Sappiamo già che il righello si deforma assumendo la forma di un’iperbole, disposta sul piano AA’E’E, dato che la luce di C deve partire in C’ per poter raggiungere, nello stesso istante di A ed E, la macchina M. Fin qui conosciamo già il gioco.

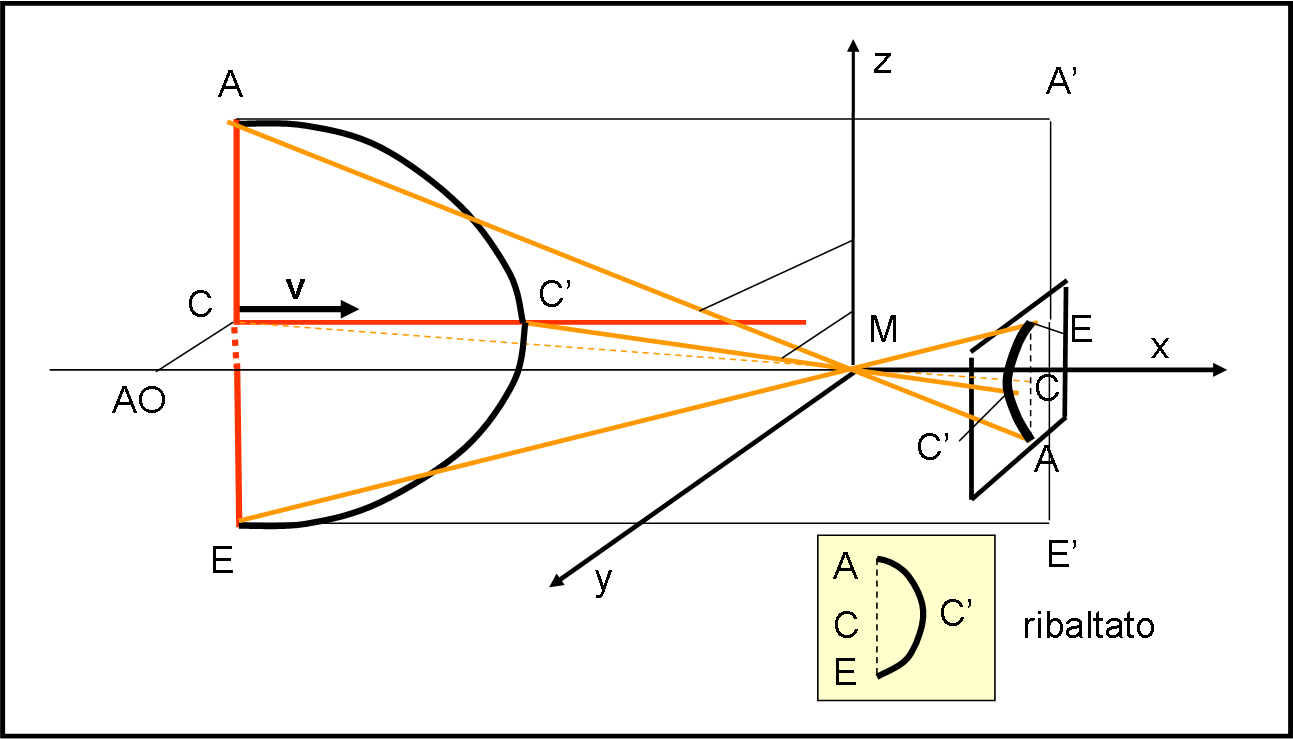
Adesso, però, vediamo tutto “fuori asse del moto” e quindi dobbiamo tenere conto dell’angolo sotto cui M vede A ed E (prima luce partita)  e poi C’, rispetto all’asse z (ad esempio). Quest’ultimo è maggiore e quindi nel piano focale C’ si sposterà lateralmente rispetto al segmento AE. Abbiamo detto che il nostro obiettivo è capace di ribaltare l’immagine ottenuta dalla camera oscura e, in conclusione, ciò che apparirà nel piano focale è un segmento curvilineo con C’ spostato verso destra, ossia verso l’esterno.

In poche parole, è come se vedessimo “di sbieco” l’iperbole descritta nel piano AA’E’E.

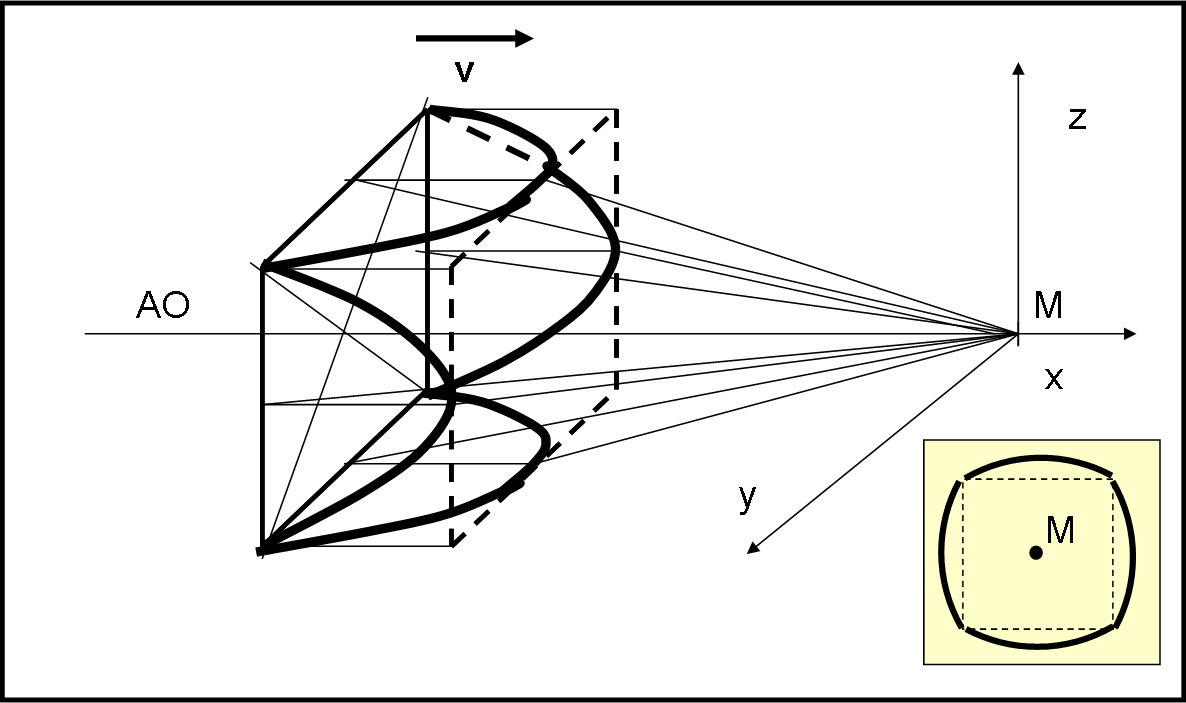
Capito questo risultato è facilissimo trasportare la soluzione al caso di un quadrato composto da quattro righelli (vuoto però!). Ogni righello si comporta come quello appena studiato, in modo anche quantitativamente simile, data la simmetria dei lati del quadrato rispetto all’asse ottico che passa per il suo centro e arriva alla macchina M. Vediamo la Fig. 2. Nascono quattro iperboli, una per lato, tutte uguali tra loro. Ognuna sarà vista di sbieco da M e quindi avrà il vertice spostato verso l’esterno. L’immagine sul piano focale di M è riportata vicino a lei: un quadrato che ha messo su molta pancia (come lo capisco…).

A questo punto possiamo anche inserire tre filmati che fanno vedere come una griglia cubica formata da righelli (un po’ più complicata, dato che abbiamo anche righelli intermedi) si vede da una telecamera posta in M, durante l’avvicinamento e l’allontanamento.

Il primo filmato riprende un avvicinamento a bassa velocità (nessun effetto relativistico, ma solo prospettico).

bassa velocità

Il secondo avviene  con una velocità pari al 90% della velocità della luce (quanto spiegato precedentemente si vede molto bene), in cui è presente anche l’allungamento dei segmenti posti parallelamente alla direzione del moto = asse ottico, capace (come abbiamo spiegato QUI) di superare la contrazione relativistica e mostrare un effetto opposto. I righelli posti all’interno dei vari quadrati danno luogo a un effetto ulteriore che spiegheremo tra poco.

altà velocità

Il terzo filmato mostra la stessa figura che si allontana con v = 0.9 c. Ovviamente, la concavità dei lati si inverte.

gitter-w0.9-xe-320x240

I filmati sono preparati dalla bravissima Ute Kraus (in attesa di quelli di … Arturo e/o Paolo).

La situazione diventa leggermente più complicata se riempiamo di “tela” il nostro quadrato di Fig. 2. In altre parole, non abbiamo solo i righelli laterali e nemmeno qualche righello intermedio (come nei filmati), ma una superficie continua (sottilissima) all’interno del quadrato. Per spiegare cosa succede in modo semplificato, ma sufficientemente corretto, consideriamo la Fig. 3.

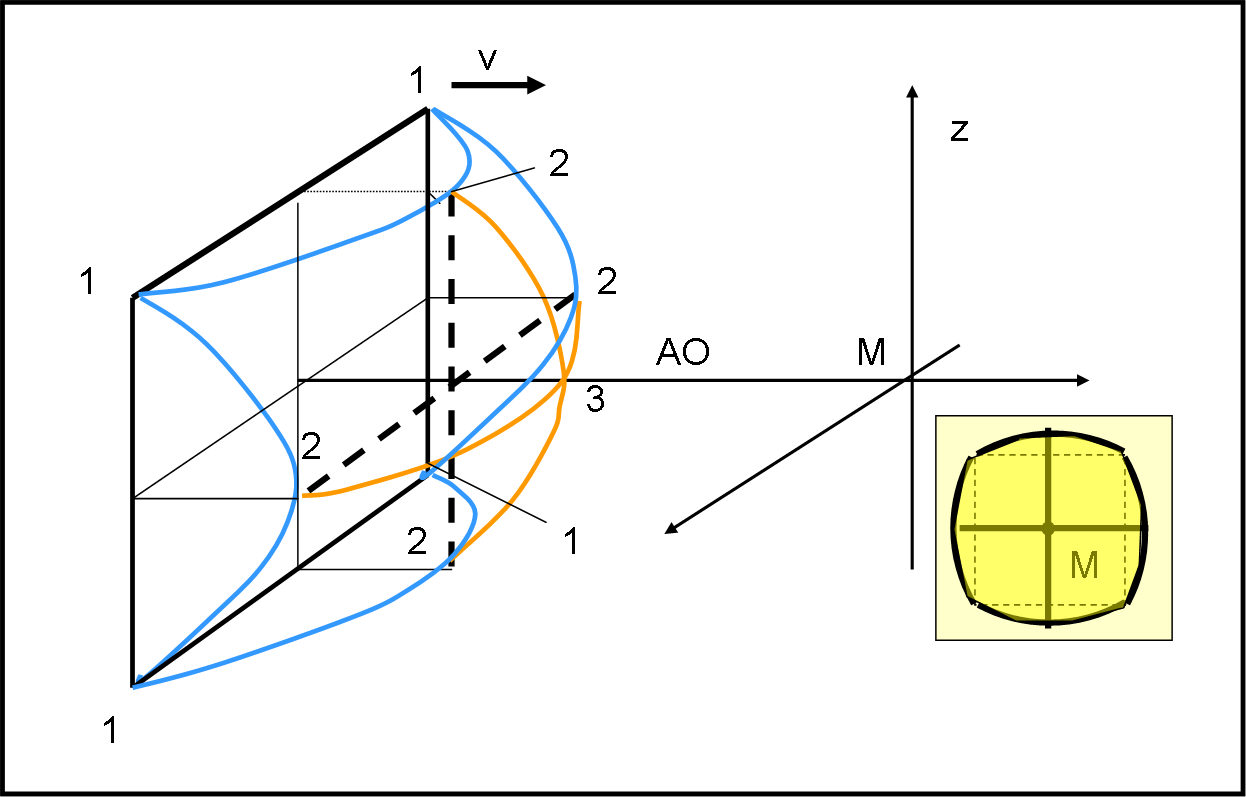
Il perimetro del quadrato corrisponde alla partenza della prima luce. Non tutta insieme, però, da come abbiamo visto precedentemente. Gli spigoli indicati con 1 sono i primi “lanciatori”, seguiti dai punti di mezzo dei singoli lati (indicati con 2). Otteniamo le curve azzurre come già ottenuto con il quadrato vuoto. Tuttavia, quando il quadrato perimetrale è giunto in 2, inizia il lancio della luce dalle parti più interne del quadrato (i loro tragitti per giungere in M sono decisamente minori). Vale la pena considerare solo le due linee tratteggiate relative ai punti di mezzo.

Il loro punto d’intersezione sta sull’asse ottico e corrisponde al tragitto più corto. Ne segue che a partire dai punti esterni della “croce” tratteggiata, si devono disegnare due iperboli che si incontrano nel punto 3, l’ultimo da cui parte la luce. La forma finale del quadrato pieno, vista lateralmente come rappresentato in figura, dà luogo a una superficie iperbolica, dato che ogni sezione ottenuta con un piano perpendicolare al quadrato (e quindi al piano focale) deve dar luogo a un iperbole (come trovato precedentemente).

Una vera e propria vela quadrata al vento, che se vista da M non si discosta molto da quanto visto precedentemente, per il quadrato vuoto. Le iperboli relative alla parte tratteggiata danno luogo a segmenti dato che hanno il loro vertice proprio sull’asse ottico (punto 3).

Ben diversa la situazione se la vela è vista da un punto qualsiasi che non sta sull’asse ottico (non ci vuole molto a immaginarsela). La vela si gonfia per effetto del vento relativistico (Fig. 4) e via verso nuove avventure! Mi sembra di vedere i nostri amici fotoni che scrutano il mare di … Dirac.

Ricordiamoci sempre che tutto questo è quello che si VEDE e non quello che si MISURA!!

 

QUI tutti gli articoli dedicati alle visioni relativistiche