Categorie: Relatività
Tags: bacherozzo buco chiodo contrazione lunghezze informazione paradossi relativistici quiz relatività ristretta rigidità simultaneità sistemi riferimento
Scritto da: Vincenzo Zappalà
Commenti:24
Soluzione del quiz del bacherozzo: cattive notizie per lui… ****
La risposta praticamente immediata di Paolo a questo quiz ha risolto brillantemente il paradosso (e vi assicuro che non era cosa facile, pur conoscendo la RR (Relatività Ristretta)). A questo punto, sembra più che giusto riportare la soluzione più generale possibile attraverso qualche formula. Non spaventiamoci: abbiamo a che fare con il solito fattore di contrazione di Lorentz e con un po’ di geometria (e fisica classica) veramente elementari, alla portata di chiunque. L’importante è riuscire a comprendere bene i concetti e seguire attentamente il ragionamento generale. Questo articolo è decisamente istruttivo per comprendere appieno la RR e può essere compreso, a livello concettuale, anche saltando i vari passaggi matematici.
Il paradosso
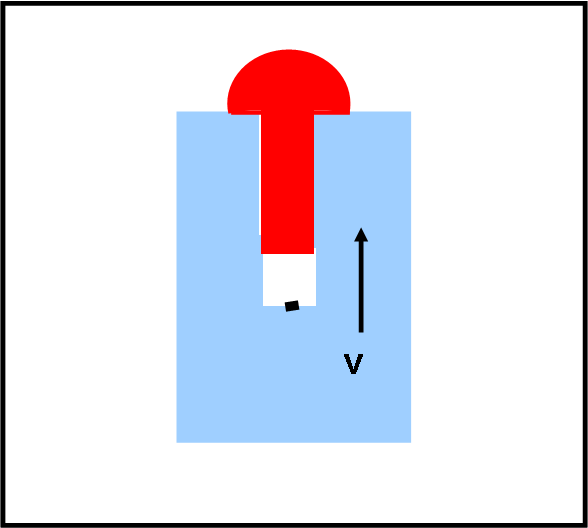
Assumiamo che il chiodo sia più corto del buco in cui si è rifugiato il bacherozzo. Vediamo di introdurre con chiarezza il paradosso che nasce in queste condizioni.
In Fig. 1 disegniamo la situazione in cui tutto è fermo.
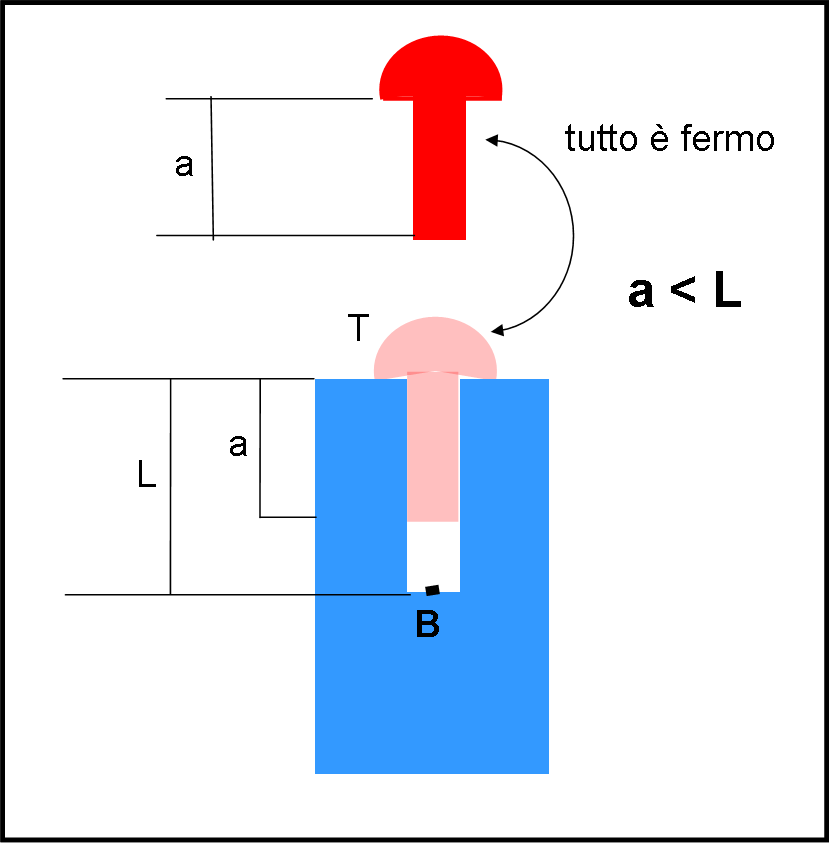
Il bacherozzo non ha nessun problema e si sente al sicuro (l’abbiamo disegnato con un piccolo trattino e indicato con B). Se il chiodo fosse inserito dentro al buco, la sua punta non lo sfiorerebbe nemmeno. Notiamo che è la posizione della testa T che determina di quanto può entrare il chiodo. In altre parole la lunghezza a (quella che interessa il bacherozzo) è la distanza tra la testa e la punta del chiodo. Non prendetemi per noioso, ma questa considerazione è molto importante. Ripetiamo ancora: è la testa che dice al chiodo di fermarsi, in quanto essa è più grande del buco.
A questo punto, entriamo nel campo della Relatività Ristretta (RR) e impartiamo al chiodo una velocità v comparabile con quella della luce c. Possiamo scrivere questa velocità come:
v = β c …. (1)
dove β può variare tra 0 e 1. Per β = 0, v = 0 e siamo nel caso degli oggetti fermi. Per β = 1, siamo nel caso in cui il chiodo viaggerebbe alla velocità della luce (limite irraggiungibile). Possiamo perciò scrivere:
0 < β < 1 …. (2)
Qualsiasi sia la velocità del chiodo data dalla (1), con i limiti imposti dalla (2), sappiamo che la lunghezza del chiodo deve accorciarsi se visto nel riferimento del bacherozzo. In altre parole, il chiodo subisce la contrazione di Lorentz che è comandata dal celebre fattore γ, dato da:
γ = 1/√(1 – β2)
La nuova lunghezza a’ del chiodo è legata a quella in quiete a, dalla ben nota formula:
a’ = a/γ = a √(1 – β2)
Il bacherozzo è ancora più rilassato di prima. La RR impone questo accorciamento e a lui non può che fare piacere (Fig. 2).
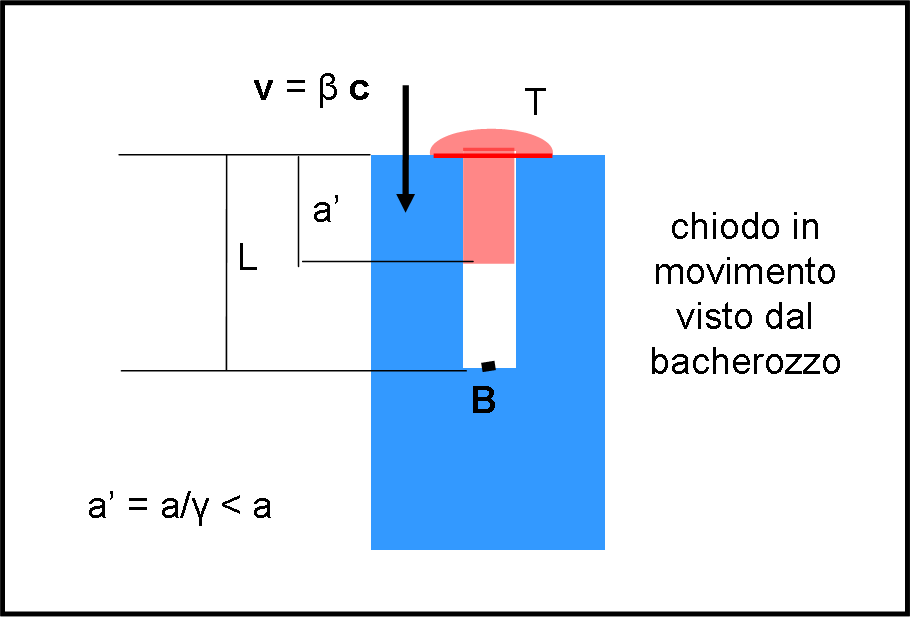
Ammettendo che la testa del chiodo “fermi” tutto il chiodo simultaneamente, il chiodo, non avendo più velocità, tornerebbe alle dimensioni che aveva quando era in quiete, comunque sempre minori del buco. Il bacherozzo non solo è salvo, ma ha apprezzato molto la RR, che gli ha mostrato una situazione ancora più favorevole. Possiamo solo dire che la testa del chiodo ha impattato il pezzo di legno a un certo istante, ma che questo fatto poco importa al bacherozzo, anzi...
ATTENZIONE: a questo punto abbiamo già accettato una caratteristica tutta da verificare. Abbiamo, infatti, considerato la lunghezza a’ come quella finale durante il moto. In altre parole abbiamo ammesso che il chiodo sia perfettamente rigido. Non spaventiamoci… ci torneremo tra poco!
Lasciamo pure ridere il bacherozzo e cambiamo sistema di riferimento, mettendoci a cavalcioni del chiodo. Per noi le sue dimensioni sono quelle iniziali (in quiete) ed è il pezzo di legno con il buco (e il bacherozzo) che ci sta venendo incontro con velocità v = β c (stesso modulo e verso opposto a prima).
Sono quindi il pezzo di legno e il suo buco che si contraggono, ossia:
L’ = L/γ = L √(1 – β2)
Per velocità sufficientemente alte, L’ diventa più piccolo di a, ossia:
L’ < a
In queste condizioni, il povero bacherozzo viene schiacciato, ancora prima che la testa del chiodo sia riuscita a impattare contro il pezzo di legno (Fig. 3). Anzi, sembrerebbe proprio che la testa del chiodo stia ben lontana dal pezzo di legno.
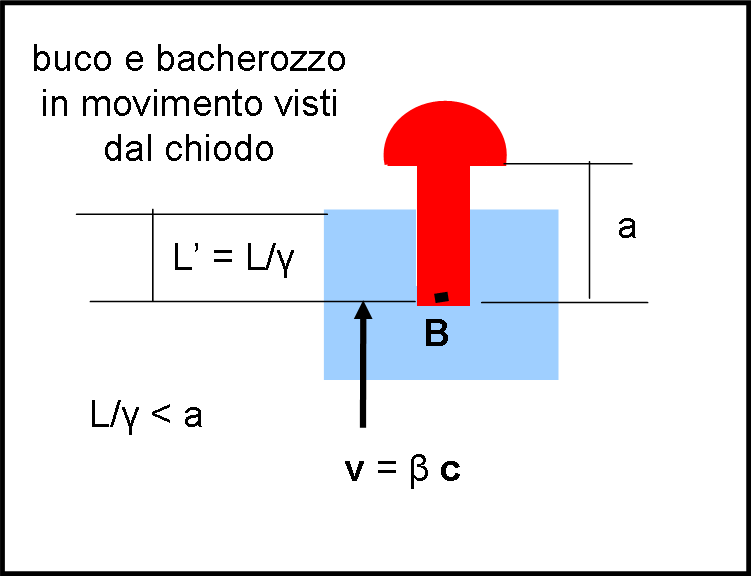
Ricapitoliamo: per certi valori di β abbiamo visto che, secondo il sistema del chiodo, il bacherozzo viene schiacciato prima che la testa possa toccare il legno. Per gli stessi valori di β (in realtà, per qualsiasi valore), secondo il sistema del bacherozzo, lui non può essere schiacciato.
La Relatività Ristretta dice però che un fenomeno fisico che avviene in un sistema di riferimento inerziale deve avvenire in qualsiasi altro sistema inerziale. I nostri due sistemi (chiodo e bacherozzo) sono inerziali… ma nel secondo il bacherozzo viene schiacciato, nel primo no! Siamo arrivati al paradosso.
Esiste un corpo rigido per la RR ?
A questo punto dobbiamo analizzare con molta attenzione una conseguenza della relatività ristretta che è molto meno conosciuta o, quantomeno, non viene compresa nel suo ruolo veramente fondamentale. Essa dice che due eventi che sono simultanei in un sistema di riferimento non lo sono più in un altro sistema di riferimento. Ciò, da solo, implica che un corpo non può essere considerato perfettamente rigido. In altre parole, l’informazione non può essere simultanea, in ogni sistema di riferimento.
E questo è un fatto che può essere ben compreso pensando alla costanza e alla limitatezza della velocità della luce. Immaginiamo un corpo perfettamente rigido. Per lui ciò che avviene a un suo estremo deve essere trasmesso immediatamente all’altro estremo. Ma ciò è impossibile, in quanto l’informazione non può certo superare la velocità della luce. Ciò comporta che un oggetto in movimento, se bloccato a un suo estremo, deve continuare a muoversi fino a che l’informazione relativa all’arresto non arrivi all’altra estremità del corpo, spostandosi alla limitata velocità della luce.
In termini più fisici, un corpo perfettamente rigido deve mantenere fisse le distanze tra i suoi atomi. Tuttavia, se noi diamo un colpetto a una sua estremità, l’informazione dovrebbe propagarsi istantaneamente al resto del corpo imponendogli di muoversi in modo da mantenere fissa la distanza tra gli atomi. La velocità dell’informazione dovrebbe, perciò, superare quella della luce. Ipotesi, questa, che non è ammessa dalla relatività ristretta.
Riassumendo: un corpo perfettamente rigido non può essere descritto dalla relatività ristretta e, perciò, non esiste nel mondo fisico.
Se queste considerazioni non sembrano semplicissime, non c’è da preoccuparsi. Hanno fatto discutere molti professionisti, stimolandoli a far cadere l’intera RR, che ne è, però, uscita ancora più forte e… rigida di prima!
L’intero paradosso si risolve proprio valutando il ritardo di un’informazione costretta a viaggiare a una velocità uguale a c, tenendo conto che v ha un valore a lei paragonabile. In qualche modo l’informazione è costretta inseguire il corpo che continua a muoversi per riuscire, finalmente, ad avvisarlo dell’evento già avvenuto.
Di nuovo nel sistema di riferimento del bacherozzo
Il primo passo è dimostrare che lo schiacciamento può avvenire anche nel sistema di riferimento del bacherozzo, malgrado lui si consideri salvo per qualsiasi valore di β. Il suo problema è che non ha tenuto conto della NON rigidità del chiodo…
Riprendiamo in mano quanto mostrato nella Fig. 2. Ciò che sicuramente capita per primo è l’urto tra la testa del chiodo e il pezzo di legno. Tuttavia, il resto del chiodo continua a muoversi alla stessa velocità v = βc. Nessuno lo ha ancora avvisato dell’avvenuto scontro della testa. Fondamentale è che l’informazione arrivi alla punta del chiodo e la immobilizzi prima che essa tocchi il bacherozzo. Vi è una corsa a due tra la punta del chiodo che si muove con v = βc e l’informazione necessaria a fermarlo, che viaggia con velocità c.
Qual è il tempo necessario affinché l’informazione arrivi alla punta?
T1 = spazio percorso/velocità
Lo spazio da percorrere è la lunghezza contratta a’, mentre la velocità è c – v (l’informazione viaggia con c, ma il chiodo gli scappa in avanti con v). Ne segue:
T1 = a’/(c – v) = a/(γc (1 – β)) …. (3)
T1 è il tempo necessario a fermare la punta del chiodo dopo che la testa ha impattato contro l’esterno del buco. Il povero bacherozzo deve sperare che non sia sufficiente a farla arrivare fino a lui. Qual è il valore limite per la sua vita o la sua morte? Non gli resta che considerare quanto spazio ha percorso la punta del chiodo durante il tempo T1. Chiamiamo D1 questo spazio.
La punta ha sempre viaggiato a velocità v, per cui:
v = D1/T1 e, ancora:
D1 = v T1 …. (4)
Il bacherozzo viene schiacciato se:
D1 > L – a’ = L – a/γ
Sostituendo il valore di D1 della (4)
Si ha:
v T1 > L – a/γ
Ricordando la (3), abbiamo:
va/(γc (1 – β)) = βca/(γc (1 – β)) = βa/(γ(1 – β))
e, quindi:
βa/(γ(1 – β)) > L – a/γ
βa/(γ(1 – β)) + a/γ > L
a/γ ((β/(1 – β) + 1) > L
a/γ ((β + 1 – β)/(1 – β)) = a ∙1/(γ(1 – β)) > L …. (5)
Prima di proseguire, scriviamo in altro modo la quantità 1/(γ(1 – β)), ricordando che 1/γ = √(1 – β2):
1/(γ(1 – β)) = √(1 – β2)/(1 – β) = √(1 + β) √(1 – β)/(√(1 – β) √(1 – β)) = √((1 + β)/(1 – β)) …. (6)
Ritorniamo alla (5), sostituendo quanto trovato nella (6):
a√((1 + β)/(1 – β)) > L
a/L > √((1 - β)/(1 + β))
(a/L)2 > (1 - β)/(1 + β) …. (7)
Dobbiamo proseguire, in quanto a noi interessa sapere il valore minimo di β, per il quale il bacherozzo viene sicuramente schiacciato. In altre parole, dobbiamo ricavare β dalla relazione precedente.
Per semplificare i passaggi, poniamo (a/L)2 = R. Questo è un parametro molto interessante in quanto a/L non è altro che il rapporto tra la profondità del buco e la lunghezza del chiodo, proprio le condizioni di partenza.
R > (1 - β)/(1 + β)
R + R β > 1 – β
β(1 + R) > 1 – R
β > (1 – R)/(1 + R) = (1 - (a/L)2)/( 1+ (a/L)2) …. (8)
Il secondo membro è il valore minimo di β (βmin) per cui il bacherozzo viene schiacciato nel suo sistema di riferimento.
βmin = (1 - (a/L)2)/(1 + (a/L)2)
Sapendo che β = v/c, ricaviamo subito il valore minimo della velocità necessario per concludere l’azione in ... tragedia.
vmin = c (1 - (a/L)2)/(1 + (a/L)2)
Il rapporto trovato nella (8) è sempre minore o uguale a 1 e ci dice la percentuale della velocità della luce che deve essere impressa al chiodo.
La validità fisica di quanto è stato ottenuto può facilmente essere confermata passando al limite.
Per a che tende a zero il rapporto tende a 1, ossia la v tende a quella della luce. Il chiodo non avrebbe praticamente una parte cilindrica e per giungere a schiacciare il bacherozzo lo stesso chiodo dovrebbe viaggiare alla velocità della luce, ossia la materia che può proseguire oltre al bordo del buco dovrebbe uguagliare la velocità dell’informazione. Per qualsiasi valore più piccolo, la “punta” del chiodo si fermerebbe subito ricevendo il segnale di “stop”.
Facendo, invece, il limite per a che tende a L, la velocità tenderebbe a essere nulla. Infatti, anche senza imprimergli velocità, il chiodo schiaccerebbe sempre il bacherozzo.
Notiamo, ancora una volta, che la testa del chiodo colpisce sempre il bordo del buco PRIMA che venga schiacciato il bacherozzo. Questo fatto ci conferma anche che il chiodo è ancora in movimento dopo l’urto della sua testa. In poche parole: urto della testa e schiacciamento del bacherozzo non sono eventi simultanei! Un riassunto dei vari istanti peculiari è riportato in Fig. 4.
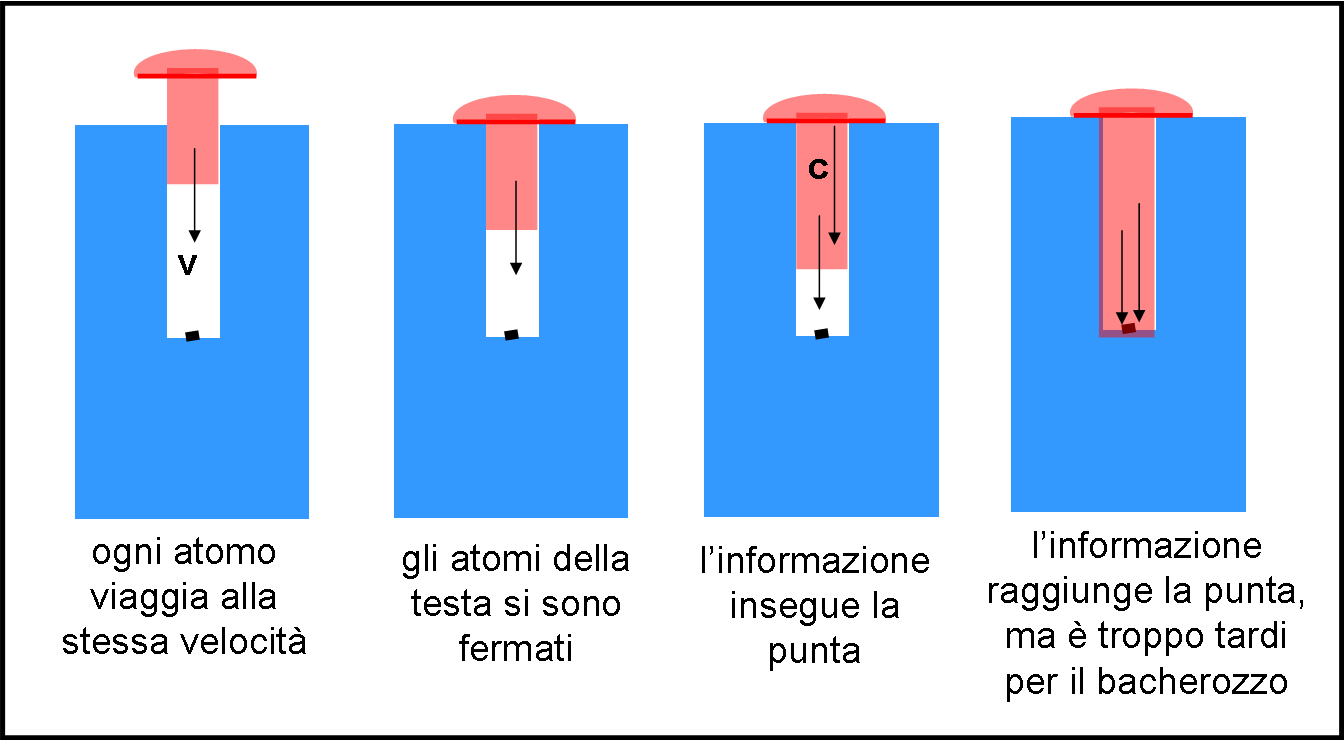
Abbiamo dimostrato che, per velocità superiori a un certo valore minimo (che dipende solo da lunghezza del chiodo e dalla profondità del buco), il bacherozzo non ha scampo.
Di nuovo nel sistema di riferimento del chiodo
Passiamo ora al sistema di riferimento del chiodo. In questo caso è il blocco di legno (con il bacherozzo) che viene verso di lui con una velocità v = β c e risulta contratto della quantità imposta dal fattore di Lorentz.
La condizione di schiacciamento del bacherozzo è immediata:
L’ = L/γ < a
Maneggiando un po’ questa relazione, si ottiene:
L√(1 – β2) < a
√(1 – β2) < a/L
1 – β2 < (a/L)2
- β2 < - 1 + (a/L)2
Cambiamo segno a tutti i termini e invertiamo la disuguaglianza:
β2 > 1 - (a/L)2
β > √(1 - (a/L)2) = βmin2 …. (9)
Confrontiamo la (9) con la (8) e si vede subito che
βmin2 > βmin
Si ottiene un risultato che non soddisfa del tutto. E’ vero che il bacherozzo viene schiacciato, comunque, ma sembra che sia necessaria una velocità maggiore di quella che abbiamo trovato prima.
Il paradosso si risolve
Prima di trarre conclusioni avventate, analizziamo meglio la situazione, dato che in questo caso abbiamo PRIMA lo schiacciamento del bacherozzo. Ma cosa capita alla testa del chiodo? Essa non urta contro il blocco di legno?
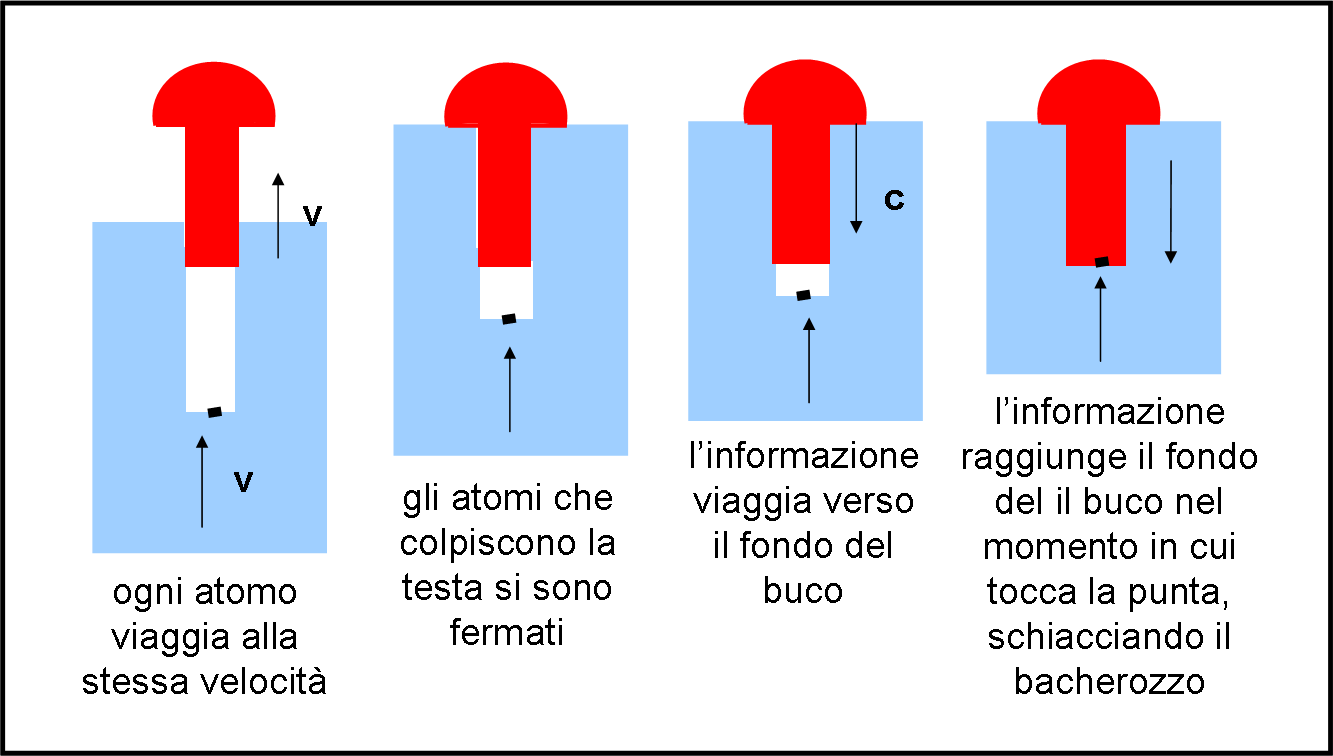
Per rispondere, mettiamoci nel caso in cui la contrazione del blocco di legno non è sufficiente per fare arrivare il chiodo a colpire il bacherozzo. In altre parole, la velocità non è abbastanza alta perché il buco si contragga fino allo schiacciamento del bacherozzo. Siamo nelle condizioni di Fig. 5, dove si nota benissimo che questa volta è nuovamente la testa a urtare per PRIMA il legno.
Gli atomi danno il segnale dello stop, ma il resto del buco (e con lui il bacherozzo) non lo sa ancora e continua a muoversi con velocità v = β c. Facciamo un po’ di conti…
Quanto tempo ci vuole affinché l’informazione che parte dal bordo del buco arrivi alla punta del chiodo? Semplice:
T2 = a/c
L’informazione viaggia, infatti, alla velocità della luce.
Durante questo tempo il fondo del buco percorre una lunghezza:
D2 = v T2 = β c a/c = βa
Ne segue che nel sistema di riferimento del chiodo (fermo) si ha lo schiacciamento del bacherozzo se:
D2 > L/γ – a
βa > L/γ – a
a(1 + β) > L/γ
a/L > 1/(1 + β) γ)
a/L > √(1 – β2)/(1 + β)
a/L > √(1 – β)√(1 – β))/(√(1 + β)√(1 – β))
a/L > √(1 – β)/√(1 + β)
(a/L)2 > (1 – β)/(1 + β) …. (10)
Fermi tutti! Paragoniamo la (10) con la (7): sono identiche per cui è inutile svolgere i passaggi successivi. Sappiamo già che valore di β troviamo…
βmin = (1 - (a/L)2)/(1 + (a/L)2)
Accidenti! Abbiamo ritrovato la stessa velocità minima ricavata nel sistema di riferimento del bacherozzo.
Un riassunto dei vari istanti peculiari viene riportato in Fig. 6.
Ne segue che se si supera lo stesso valore della velocità, il bacherozzo viene schiacciato sia nel suo sistema di riferimento che in quello del chiodo.
Il paradosso è stato completamente risolto! Infatti, lo stesso identico fenomeno avviene in entrambi i sistemi di riferimento, imponendo la stessa velocità.
Analisi finale
Possiamo ancora fare alcune importantissime considerazioni.
Notiamo che in entrambi i sistemi l’urto tra la testa del chiodo e il bordo del buco avviene per PRIMO se:
βmin < β < βmin2
Infatti, se β > βmin avviene sicuramente per primo l'evento "urto della testa", nel sistema del bacherozzo (come abbiamo dimostrato precedentemente).
Tuttavia, sappiamo anche che se β < βmin2 non è possibile che l'evento "schiacciamento del bacherozzo" avvenga per primo, nel sistema del chiodo (come abbiamo dimostrato precedentemente) e quindi anche in questo caso abbiamo per primo l’urto della testa.
Se non capita quanto appena detto (β > βmin2), i due sistemi, pur ammettendo che il bacherozzo venga schiacciato, differiscono nella conclusione su quale evento avvenga per primo: l’urto della testa (sistema del bacherozzo) o lo schiacciamento del bacherozzo (sistema del chiodo)
Poco male, dato che il fatto è CONSISTENTE con la Relatività Ristretta, che si basa proprio sulla relatività della simultaneità!
C’è poco da fare… dilatazione dei tempi, contrazione delle lunghezze sono ricadute molto importanti, ma nascono entrambe dalla vera base della RR: la relatività della simultaneità. Se non si comprende bene questo concetto, la RR mantiene sempre qualche lato oscuro o fa cadere, prima o poi, in confusione. Qualsiasi paradosso si può risolvere solo e soltanto considerando questo concetto base, compreso quello celeberrimo dei gemelli!
Terminiamo con una caso particolare che aiuta ancora meglio a capire queste ultime frasi.
Ammettiamo che β sia proprio uguale a βmin2. Siamo in condizioni peculiari, in quanto i due eventi sopra citati avvengono nello stesso istante nel sistema del chiodo (esso riempie perfettamente il buco nello stesso istante). Non lo sono, invece, nel sistema del bacherozzo.
Capiti perfettamente i concetti esposti in questo splendido paradosso, la maggior parte degli altri diventano giochi da ragazzi (e lo proveremo…).
Buone vacanze a tutti! Il Circolo non va in vacanza, ma continua con argomenti più “leggeri”…






24 commenti
Non fatevi spaventare dalle formule... dovevo metterle per dimostrare come il paradosso si risolva quantitativamente, ammettendo che in RR non può esistere un corpo rigido. Tuttavia, anche senza seguire le formule, le varie conclusioni seguono un discorso che aiuta perfettamente a capire il concetto di fondo, anche in modo del tutto qualitativo.
Cercate di fissarvi su quello e molti altri paradossi si scioglieranno come neve al Sole... La chiave di tutto è sempre e soltanto la relatività della simultaneità! Nemmeno lo stesso Einstein aveva capito fino a che punto avrebbe permesso di descrivere la realtà fisica...
Ancora una volta un quiz che ci invita a ragionare su conseguenze della RR meno note, ma che mi sono parse fondamentali per capirne il significato. Grazie ad Enzo e complimenti a Paolo per l'intuizione della soluzione.
Andando nel dettaglio della soluzione qualche dubbio mi è venuto.
Uno viene dal confronto delle due ultime immagini delle figure 4 e 6, che chiamo 4.4 e 6.4. Il chiodo sembra essere di lunghezza diversa nelle due immagini. Nella figura 4.4 la lunghezza è L, mentre nella 6.4 la lunghezza sembra essere a (solo per β=βmin a=L/γ) poichè è la base del foro che raggiunge la punta del chiodo.
Pur venendo da storie diverse, le due immagini mi sembra rappresentino la stessa situazione fisica vista dal medesimo riferimento. A quel punto chiodo e foro sono ormai solidali cosi come lo sono i relativi sistemi di riferimento. In questa situazione avere lunghezze diverse nelle due immagini per lo stesso oggetto mi sembra possa essere un problema.
Cercando di trovare una spiegazione a questo situazione ho notato che solo uno dei due riferimenti di fig. 4 e 6 può essere inerziale perché la loro velocità relativa varia. Mi sembra ragionevole considerare inerziale il riferimento del foro (fig.4) e non inerziale quello della testa del chiodo (fig.6).
Per evitare i problemi di un cambio di riferimento inerziale ho cercato di vedere il risultato continuando a ragionare sul riferimento inerziale che inizialmente era della testa del chiodo, che chiamo riferimento 2. Il riferimento 1 è quello del foro.
Mi vengono questi diagrammi di Minkowski per il riferimento 1 e 2.
Nel riferimento 1 la lunghezza finale del chiodo quando β≥βmin è sempre L.
Nel riferimento 2 è sempre L/γ quando β≥βmin. La cosa mi sembra coerente poiché il chiodo alla fine è fermo rispetto al riferimento 1 e si muove con velocità -β rispetto al riferimento 2.
L'equivalente delle figure 6 e 4 nel riferimento 2 potrebbe essere questa:
In questo riferimento il foro continua a procedere con velocità -β ed il bordo del foro trascina la testa del chiodo. La punta del chiodo rimane ferma fino a che non incontra la base del foro.
Rimane da verificare come si presenta il fenomeno visto dal riferimento non inerziale della testa del chiodo. In questo riferimento c'è un repentino cambiamento quando testa del chiodo e bordo del foro vengono a contatto. Prima era il foro che si muoveva con velocità -β ed il chiodo era fermo, poi il foro è fermo ed il chiodo (almeno gran parte) si muove con velocità β. Se a questo cambiamento corrispondono gli usuali effetti sulle lunghezze la figura 6 potrebbe diventare questa:
Qui ovviamente è la testa del chiodo che rimane ferma e mantiene fermo anche il foro da quando viene a contatto con il bordo. La punta inizia a procedere con velocità β fino a che non riempe tutto il foro o viene raggiunta dalla informazione sul mutamento dello stato di moto della testa.
Tutto questo mi porta a pensare che è plausibile che la lunghezza del chiodo nelle immagini 4.4 e 6.4 dovrebbe essere uguale e pari ad L.
Non vedo invece effetti sul calcolo di βmin
caro Fabry,
innanzitutto tieni conto che le figure non sono state fatte mantenendo le giuste distanze, ma solo il concetto qualitativo.
l'importante è che nella Fig. 4, il blocco di legno è fermo e quindi non può cambiare dimensioni. Fino a un certo punto tutto segue la classica RR e il chiodo entra tranquillamente con la sua contrazione costante. Quando la testa viene a contatto col legno, inizia la deformazione per mancanza di rigidità. La vite continua ad allungarsi e per certi valori di beta non gli viene indicato lo stop in tempo per evitare di toccare il fondo. Toccando il fondo il sistema chiodo è fermo e tornerà alle dimensioni iniziali. Chiaramente si può intendere che al momento dell'urto della testa, il sistema non sia più inerziale e vi sia una decelerazione. Tuttavia, pur senza passare alla RG si può benissimo darne una spiegazione fisicamente accettabile.
Cosa analoga nella Fig. 6. Qui è il chiodo che è sempre fermo e sempre uguale. E' il legno che si contrae normalmente seguendo la RR. Ma, quando la testa subisce l'urto è il blocco di legno che inizia a deformarsi perché ancora non gli è arrivato il segnale di stop. Esso potrebbe arrivare dopo che il chiodo tocchi il fondo, oppure, come indicato nel testo, esattamente nello stesso istante, ossia sarebbero simultanei nel sistema chiodo.
La tua figura 2 mi sembra perfettamente in linea. Nell'ultima, invece, è solo il legno che deve accorciarsi sempre più fino a che non gli arrivi lo stop dalla parte che tocca la testa del chiodo... Il sistema di riferimento rimane il chiodo sempre uguale di lunghezza. Anche in questo caso, una volta che il legno è arrivato allo stop finale, torna alle dimensioni inziali...
Sempre che abbia capito i tuoi dubbi...
Caro Fabry,
ti consiglierei di affrontare il nuovo quiz sulla macchina e il garage... usando Minkowski. La prima parte è estremamente facile, ma - bloccando la seconda porta- ci ritroviamo in una situazione simile a quella del bacherozzo... ma ancora più nitida (e semplice).
Caro Enzo,
quello che dici mi sembra confermare che le lunghezze della vite nelle ultime immagini della fig.4 e della fig.6 sono diverse.
Al termine della sequenza di figura 4, per β≥βmin, la vite assume la lunghezza L del foro. Nella figura 6 la vite rimane della sua lunghezza iniziale che è a ed è il foro che si deforma assumendo la lunghezza della vite.
E' proprio questa differenza di lunghezze che non mi convince. Le ultime immagini delle due sequenze riprendono la stessa situazione fisica vista dallo stesso riferimento. A quel punto chiodo e foro sono diventati solidali cosi come i rispettivi riferimenti. In entrambe le immagini il chiodo è fermo rispetto al riferimento.
caro Fabry,
certo che non sono uguali...
Nella prima è il chiodo che si muove e può fermarsi solo quando gli arriva il segnale. Nella seconda, invece, è fermo e quindi deve mantenere la sua lunghezza fissa. Si possono deformare solo gli oggetti che si stanno muovendo, ma per i quali lo stop non è simultaneo tra testa e coda. Lo stesso succede anche al pezzo di legno, costretto a schiacciarsi ancora di più della sua contrazione relativistica. In poche parole, oltre alla RR cinematica dobbiamo tenere conto che i corpi non possono essere rigidi (lunghezza contratta fissa), ma devono allungarsi o schiacciarsi fino a che non arriva il segnale di stop.
Tieni anche conto che gli oggetti fermi sono considerati inamovibili per definizione. Il che vuol dire che se qualcosa viene bloccato da un limite inamovibile, può considerarsi fermo e riprende le dimensioni a riposo.
Scusa se insisto ancora.
Nella 4a immagine delle fig.4 e 6, abbiamo uno stesso oggetto, la vite, vista da due riferimenti nei quali è per entrambi ferma.
E' vero che la storia dei due riferimenti è diversa, ma alla fine la lunghezza in un riferimento nel quale l'oggetto è fermo corrisponde alla distanza nello spazio 4-dim che non dipende dal riferimento e dalla sua storia. Per questo la lunghezza della vite (stesso oggetto) valutata nei due riferimenti dovrebbe essere la stessa (per β≥βmin credo sia L), indipendentemente dalle vicissitudini che hanno portato all'oggetto ad avere quella lunghezza.
Anche se in uno dei due riferimenti la vite fosse in moto con velocità β la relazione tra le lunghezze nel riferimento fermo e quello in moto non potrebbe essere arbitraria come è la relazione tra L e a.
Cerco di argomentare anche la differenza che vedo nella rappresentazione di fig.6.
Dopo il contatto tra bordo del foro e tasta della vite, nel riferimento di fig.6 solidale con la testa della vite, a mio parere, si muove la punta della vite verso il basso e la base del foro rimane ferma a distanza L dall'entrata del foro.
Nel momento del contatto ci sono due effetti rappresentati in fig.6. C'è un cambio di riferimento inerziale poichè passiamo dal riferimento in movimento con la vite al riferimento del blocco. C'è un effetto, che chiamerei dinamico, del aggancio della testa della vite sul bordo del foro. (nella fig.4 invece non c'è il cambio di riferimento).
Il cambio di riferimento non ha tempi di propagazione. Il suo effetto è immediato nella rappresentazione che diamo. Nel nuovo riferimento inerziale tutto il blocco è fermo e, quindi, lo è anche il fondo.
Cosa diversa è per l'effetto dinamico sulla vite. E' sola la testa del foro che ha subito l'effetto del contatto. Questo si propaga sul resto della vite con velocità non superiore a c. Quindi la punta della vite, che nel nuovo sistema di riferimento si muove verso il basso, continua a farlo finché tocca il fondo o gli arriva l'informazione.
Non so più che dire...
Ogni atomo della vite che si muove, ha una velocità v e il corpo può anche immaginarsi rigido. Adesso blocchiamo una sua parte, o la testa o la coda, poco importa. Se gli eventi "blocca la testa" e "blocca la coda" fossero istantanei la vite si fermerebbe all'unisono e riprenderebbe la forma originaria non soggetta alla RR. Se, invece, uno dei due eventi avviene prima, l'altra parte deve aspettare di sapere cosa è avvenuto e l'unica cosa che può dirglielo è l'informazione che si propaga, alla velocità della luce, da un atomo all'altro. Nel frattempo le distanze tra atomi si allungano (o si accorciano), dato che i primi (o i secondi) cominciano a fermarsi e gli altri no. In certi casi vi è dilatazione (testa bloccata), in altri contrazione (punta bloccata). Questo è un fenomeno che entra nella dinamica e che inserisce in qualche modo la RG (accelerazione o decelerazione). Tuttavia, assumendo la rigidità come una situazione non ammessa dalla RR, si può tranquillamente lavorare solo con lei. La vite può anche assumere alla fine della trafila una lunghezza momentanea diversa, se è lei che si muove oppure no, ma raggiunto lo stop completo tutto torna come all'inizio.
Posso dirti che questo tipo di spiegazione non ha mai convinto tutti e alcuni introducono la fisica degli urti e le accelerazioni. Io, invece, penso che dia una spiegazione conforme alla RR, senza aver bisogno di RG, come in fondo capita anche nel paradosso dei gemelli.
Teniamo, inoltre, conto che le soluzioni momentanee finali dipendono dalla beta che dipende da a e D iniziali... Ogni caso ha la sua velocità limite per far succedere una cosa o l'altra.
L'ultima immagine della 4 vale per il solo istante in cui arriva lo stop, poi la vite riprende la sua dimensione (solo in quel momento è ferma... prima viaggiava, almeno in parte, a velocità v). Nella Fig. 6 la vite è sempre ferma e quindi deve sempre avere un valore fisso (rigido). Durante il moto della vite in un sistema è contratta, nell'altro no... eppure accettiamo questa conclusione relativistica...
"Dopo il contatto tra bordo del foro e testa della vite, nel riferimento di fig.6 solidale con la testa della vite, a mio parere, si muove la punta della vite verso il basso e la base del foro rimane ferma a distanza L dall'entrata del foro."
Come potrebbe muoversi la vite che è ferma per definizione? Lei deve rimanere ferma e rigida. L'unica cosa che si sta muovendo è il blocco di legno: è la sua parte posteriore che si ferma, ma quella in basso non può ancora saperlo e continua nel suo moto fino a che gli arriva il segnale o fino a che non vada comunque a sbattere contro la punta della vite (dipende dalle condizioni iniziali e di conseguenza dalle beta usate).
Nel momento del contatto ci sono due effetti rappresentati in fig.6. C'è un cambio di riferimento inerziale poichè passiamo dal riferimento in movimento con la vite al riferimento del blocco. C'è un effetto, che chiamerei dinamico, del aggancio della testa della vite sul bordo del foro. (nella fig.4 invece non c'è il cambio di riferimento).
Perché c'è il cambio? Siamo sempre nel sistema della vite ferma e l'unica cosa contratta che riesce ancora a muoversi è il blocco di legno... Non riesco a capire perché vuoi cambiare il sistema. Per la vite è il blocco che si muove e deve continuarlo a fare anche dopo che la parte superiore ha toccato la vite. A meno che le due cose siano istantanee (ma è un caso particolare, come abbiamo visto).
Tu dai ferma per definizione la vite nel suo complesso nel sistema di riferimento di fig.6.
Io do ferma per definizione la testa della vite. Finchè la punta della vite procede alla stessa velocità della testa anche la punta è ferma. Quando la punta non ha più la stessa velocità della vite dopo il contatto testa-blocco, la punta non è più ferma.
Proprio perchè il blocco continua a muoversi indisturbato, nel sistema di riferimento della testa della vite è fermo dal momento che la testa della vite viene a contatto con il bordo del foro.
Nel momento del contatto testa-vite c'è un cambio di riferimento inerziale per la testa della vite. La situazione mi sembra simile a quella del paradosso dei gemelli quando il gemello che viaggia inverte la rotta. Come nel caso dei gemelli il blocco di legno e la testa della vite non vivono due situazioni simmetriche.
La ragione che mi sembra avvalori questi cambi è che alla fine portano ad una situazione nella quale la vite vista da un sistema di riferimento nella quale è ferma ha sempre lunghezza L. Se seguo l'altro ragionamento, più simmetrico tra comportamento del blocco e della vite, si arriva ad una situazione nella quale la lunghezza dello stesso oggetto, la vite, in due riferimenti nella quale è ferma, risultano diverse.
scusa Fabrizio, ma continuo a non capire come un sistema considerato fermo possa improvvisamente trovarsi in movimento. Un cambio di sistema che reputo del tutto inutile. La differenza di lunghezza della vite , come del blocco, dipende dal fatto che uno ha una certa velocità e l'altro no e quindi subisce una deformazione dovuta alla non rigidità. Se a un certo punto viene raggiunta una lunghezza diversa non mi sconvolge più di tanto, dato che è una cosa temporanea dovuta alla non rigidità.
Posso anche convenire con te che anche qualcosa di fermo possa essere schiacciato o deformato e può essere accettabile (vedi Fig. 3). In quel caso possiamo anche pensare che la vite si accorci e non il blocco, ma... direi che cambia poco...
Forse sono due modi diversi per vedere la stessa cosa. Tu pensi tanto alla vite, ma perchè il blocco dovrebbe fermarsi e non schiacciarsi?
mettiamola così Fabry,
nel sistema che uso io... la vite può diventare lunga come il buco (L) e il buco può diventare corto come la vite (a), a seconda del sistema usato.
Tu vorresti, invece, che entrambi arrivassero a una stessa lunghezza (che non è quella a riposo). Ma, allora, perché deve essere L e non a? sono entrambe lunghezze stabilite fin dall'inizio. Per quale motivo la vite dovrebbe sempre arrivare a essere lunga L? E non invece entrambi alla lunghezza a? Non vedo differenza, così come non la vedo se le lunghezze raggiunte prima del ritorno al riposo fossero diverse tra loro...
Credo che l'assunzioni implicita della fig.4 è che la massa del blocco (MB) sia molto maggiore della massa della vite (MV). Per questo in fig.4 il blocco rimane fermo e la vite assume alla fine la lunghezza L.
Con MB<<MV avremmo la situazione contraria ed alla fine sarebbe la lunghezza del foro ad allinearsi con la lunghezza a della vite. Credo sia questa la situazione descritta nell'attuale fig.6.
In termini di riferimento inerziale la situazione non è simmetrica. C'è uno dei due elementi che si mantiene su un riferimento inerziale, mentre l'altro lo cambia a partire dal punto di contatto.
Ho capito cosa intendi... il blocco trascina con sé la vite e la mette in moto ... No, io intendevo che ciò che è il sistema considerato fermo, deve rimanere fermo, indipendentemente dalla sua massa. Altrimenti il problema diventa un problema di dinamica, dato che la vite che viene messa in moto acquista una velocità a partire da zero, ossia accelera. D'accordo che esiste, comunque, una decelerazione, ma è mascherata dall'arrivo dell'informazione che blocca atomo per atomo...
Tutto sta nel modo di affrontare il problema. Quello che interessa, nelle mie ipotesi, è dimostrare che ciò che capita in un sistema, capita anche nell'altro e che la simultaneità è relativa.
Probabilmente, è veramente un paradosso che vede molte vie di soluzione...
Forse è meglio affrontare l'altro, decisamente meno ingarbugliato...
E' proprio quello che ho imparato da questo quiz. Alle contrazioni di Lorenz si possono aggiungere altri effetti dinamici dovuti alla propagazione della informazione.
Passo all'altro quiz.
caro Fabry,
e, spesso, sollevano ancora dubbi e idee diverse, come abbiamo dimostrato anche noi, nel nostro piccolo. E' ammissibile avere lunghezze diverse e restare nella RR? Chi è fermo resta fermo o subisce forze, passando alla RG? E via dicendo... In realtà, la trattazione migliore, ma molto complicata, è passare decisamente a una barra accelerata, tenendo conto degli urti... Sembra facile a prima vista, ma poi bisogna essere veri specialisti e non basta ancora...
Beh... l'altro sarà per te una passeggiata...
Confesso che ho affrontato lo studio della soluzione di questo quiz con un po' di diffidenza perché temevo che mettesse in crisi il concetto di lunghezza propria che ogni oggetto mantiene nel proprio sistema di riferimento, anche se si muove a velocità relativistica.
Apprendo, invece, con sollievo, che la sorte del bacherozzo dipende solo e soltanto dalla lunghezza propria della vite, dalla lunghezza propria del buco e dalla velocità alla quale ognuno dei due si muove rispetto all'altro: nelle formule il fattore di Lorentz scompare (e, con esso, la contrazione apparente misurata dall'osservatore "fermo") e l'esito finale è figlio della non rigidità dei corpi.
La cosa apparentemente sorprendente è che ciò si può dimostrare partendo proprio dalle formule della RR...
Ho compreso bene o qualcosa mi sfugge?
Dici bene Daniela... teniamo però conto che la non rigidità è figlia diretta della non simultaneità. Un corpo è costretto ad aspettare che la luce gli mandi l'informazione e tutto ciò dipende dal sistema di riferimento scelto.
Dimostrata la non rigidità è anche ovvio che i corpi possano deformarsi fisicamente durante il processo di sincronizzazione relativa (chiamiamola così...). Ma poi tutto torna a posto, quando lo stop è arrivato. E i tempi di stop come dici bene tu dipendono solo dalla velocità che a sua volta dipende dai dati "statici" del problema.
Tra poco vedremo un caso in cui è proprio la lunghezza propria che si riduce, ammettendo un blocco insormontabile. Ma, come sempre, allo stop tutto deve tornare in quiete.
Vorrei, se posso, fare delle domande.
Spero di non andare troppo fuori tema o complicare troppo la cose.
Allora, se ho capito bene, un corpo che ha rigidità assoluta, in realtà, non esiste, neanche teoricamente (va contro i principi della RR).
Se io fermo la testa del chiodo, la punta prosegue il moto finché non le arriva l’informazione di arresto, e questo avviene alla velocità della luce.
Allora facciamo un esempio più generale.
Prendiamo una astronave molto lunga che viaggia a una velocità v rispetto a un sistema in quiete.
Adesso facciamo decelerare istantaneamente il dietro dell’astronave (i motori sono fisicamente applicati in quella zona).
Ne consegue che il davanti continua il moto per un certo tempo portando all’allungamento fisico dell’astronave.
Prima domanda: l’informazione di arresto viaggia sempre alla velocità della luce o anche più lentamente, in base al materiale dell’astronave stessa, nel caso non fosse assolutamente rigida (per la meccanica classica)?
Seconda domanda: l’astronave si allunga ma non si spezza mai? Se fosse assolutamente rigida a livello di materiale è previsto che si spezzi qualsiasi sia l’allungamento?
Terza domanda: Sempre considerando che il materiale sia assolutamente rigido, una vota arrivata l’informazione di arresto in testa all’astronave, quest’ultima resta snervata, o ritorna alla sua lunghezza originaria? (Questo non l’ho sinceramente capito).
Quarta domanda: Se ritorna alla sua lunghezza originaria, come lo fa, cioè la testa ritorna invertendo il moto, quindi nuova accelerazione per poi decelerare? Si può comportare come una molla, ovvero può oscillare teoricamente molte volte? Ma se l’astronave non è vincolata a nulla qual è il punto (il baricentro) di oscillazione?
Quinta domanda: Ma se il fondo dell’astronave si ferma, e la testa no, diventano due sistemi di riferimento separati con le loro differenti simultaneità? Ovvero chi sta in fondo come vede scorrere un orologio posto in testa, e le lunghezze? (Questa è la domanda che mi preme di più).
Spero di non abusare troppo della tua pazienza, e spero di essere stato chiaro nelle domande.
Comunque, nessuno è veramente sicuro di quello che succeda realmente... non vi sono mai stati esperimenti di questo tipo...
Ti ringrazio per la risposta.
Ho capito che l’argomento è molto complesso, e probabilmente non ha risposte assolute e univoche.
Spero che in futuro tratterai l’accelerazione relativistica e i moti iperbolici in modo più approfondito.
Tra l’altro mi hai già risposto alla domanda che ti avrei fatto successivamente, ovvero non sono mai stati fatti esperimenti a tal proposito?
Quindi tu mi dici di no… strano però, con orologi atomici, sistemi di misura di una precisione incredibile non servirebbero velocità estremamente elevate per avere delle misurazioni percettibili e quantificabili, o forse sì.
Quindi noi (inteso in generale) stiamo a parlare di materia oscura, energia oscura, dimensioni multiple, teoria delle stringhe o altro, quando in realtà non siamo del tutto sicuri neanche di cose vecchie più di un secolo, che dovrebbero essere ormai consolidate, come la relatività.
Questo diventa un vero paradosso nel paradosso, o almeno vedere persone che hanno una sicurezza assoluta su tutto, che poi in realtà più indaghiamo in profondità e più la cosa diventa complessa e a tratti assurda: la MQ è un esempio lampante.
Va bene, questi sono pensieri miei, spero di non aver stancato…
caro Simone,
non è tanto se la RR funziona o no (questo è assodato), ma quali siano le sue realistiche ricadute fisiche. Gli esperimenti devono portare qualcosa di macroscopico a velocità prossime a quella della luce. E questo è ancora un bel problema! In parole povere: la contrazione di Lorentz è un'apparenza legata al sistema o è un processo fisico?