Per una trattazione completa dell'entrata nel buco nero, si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

Non è molto che abbiamo descritto un viaggio verso un buco nero. Eravamo arrivati al bordo dell’orizzonte degli eventi, ma non eravamo entrati veramente nelle “fauci del mostro”. E' venuta l'ora di bussare a quella porta che lascia entrare, ma non uscire...

Ciò che si “vede” all’interno dell’orizzonte degli eventi, non può essere descritto attraverso gli effetti a cui siamo abituati quotidianamente e che -pur se con difficoltà- possiamo ancora usare per altri fenomeni celesti di immane energia. L’interno di un buco nero è un altro Universo, dove spazio e tempo perdono il significato che conosciamo normalmente. Dovremmo cambiare i nostri occhi e tutte le sensazioni per descrivere la fenomenologia che avviene.

Potremmo dire che la forza di marea causa la “spaghettificazione” delle cose, allungando la materia in una sola direzione, quella che termina inesorabilmente nella singolarità finale (QUI abbiamo parlato della "spaghettificazione" del campo magnetico generato da un buco nero galattico). Oppure che è necessario un terzo occhio per vedere. O ancora che la curvatura dello spazio-tempo diventa infinita. E che dire dello sdoppiamento dell’orizzonte? Parole di effetto, ma con poco riscontro razionale.

Molto meglio prendere il “toro per le corna” e descrivere cosa sia in realtà un buco nero nell’insieme generale dello spaziotempo, rappresentandolo graficamente in un diagramma bidimensionale, perfettamente logico e preciso, in cui un concetto aleatorio e intangibile come l’infinito sia “facilmente” e concretamente rappresentabile.

Prima di iniziare, dobbiamo fare un’ipotesi importante. Ciò che andremo a trattare si riferisce al caso puramente teorico del buco nero statico di Schwarzschild. Esso non ha rotazione e nemmeno carica elettrica.

I buchi neri stellari nascono due volte…

La prima volta, da tempo immemorabile, attraverso il collasso gravitazionale di una stella dell’Universo molto più massiccia del Sole.

La seconda volta quando, poche settimane dopo la pubblicazione della Teoria della Relatività Generale di Einstein, Schwarzschild introduce la sua geometria capace di descrivere lo spazio vuoto che circonda una massa sferica. Pur se relativamente limitata, essa si basa, ovviamente, sulla soluzione delle equazioni di Einstein e la sua applicazione a masse diverse ha messo in luce un raggio critico al di sotto della quale nessuna informazione può più uscire.

Al suo interno, le curve tipo spazio dello spaziotempo di Minkowski diventano linee tipo tempo e qualsiasi linea di Universo è costretta a terminare nella singolarità centrale. Questo raggio prende il nome di raggio di Schwarzschild e se una massa è contenuta completamente all’interno di essa, prende il nome di buco nero, per ovvie ragioni ormai note a tutti. A titolo di esempio, per una massa pari a 30 masse solari, il raggio di Schwarzschild non supera i 100 km.

E’ solo per una curiosa e fortunata coincidenza che questo raggio sia già stato derivato nel 1783, da John Michell, nell’ambito della teoria newtoniana e della natura corpuscolare della luce. In quel caso il raggio critico è quello che deriva dalla velocità di fuga posta uguale a quella della luce, per un corpo di massa M e di raggio r.

Come ormai sappiamo bene (QUI e QUI) nel caso newtoniano è comunque possibile uscire “gentilmente” da tale oggetto celeste, mentre nel caso relativistico non vi è alcuna possibilità.

La geometria di Schwarzschild è illustrata abbastanza bene da un diagramma a due dimensioni che  rappresenta una geometria spaziale a tre dimensioni in un particolare istante t. Esso nasce praticamente attraverso una specie di “matrioska” sferica (ogni sfera è contenuta in un’altra con lo stesso centro, Fig. 1). Si inseriscono particolari coordinate che portano a uno sviluppo su un piano.

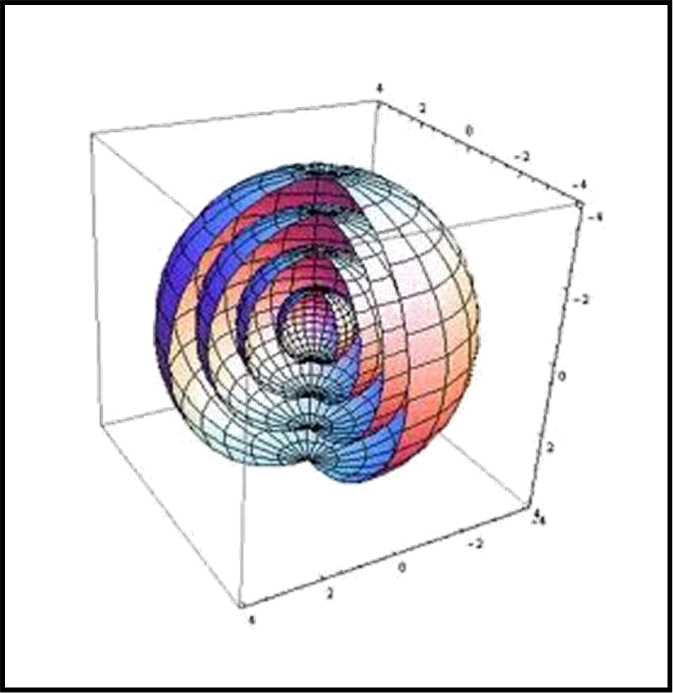
Il suo aspetto finale ricorda molto quello che avevamo criticato come fuorviante nell’ambito della comune descrizione dei buchi neri, simili a imbuti in cui cade la materia (QUI). Una cosa è però “credere” che lo spazio sia un tessuto bidimensionale che si piega e un’altra è una rappresentazione matematica e geometrica che descriva le caratteristiche dello spazio tempo attorno una massa sferica. Purtroppo la metrica di Schwarzschild è un po’ troppo ardua per il nostro blog e dobbiamo accettarne i risultati. Ne diamo una rappresentazione di massima, senza entrare nei particolari, nella Fig. 2.

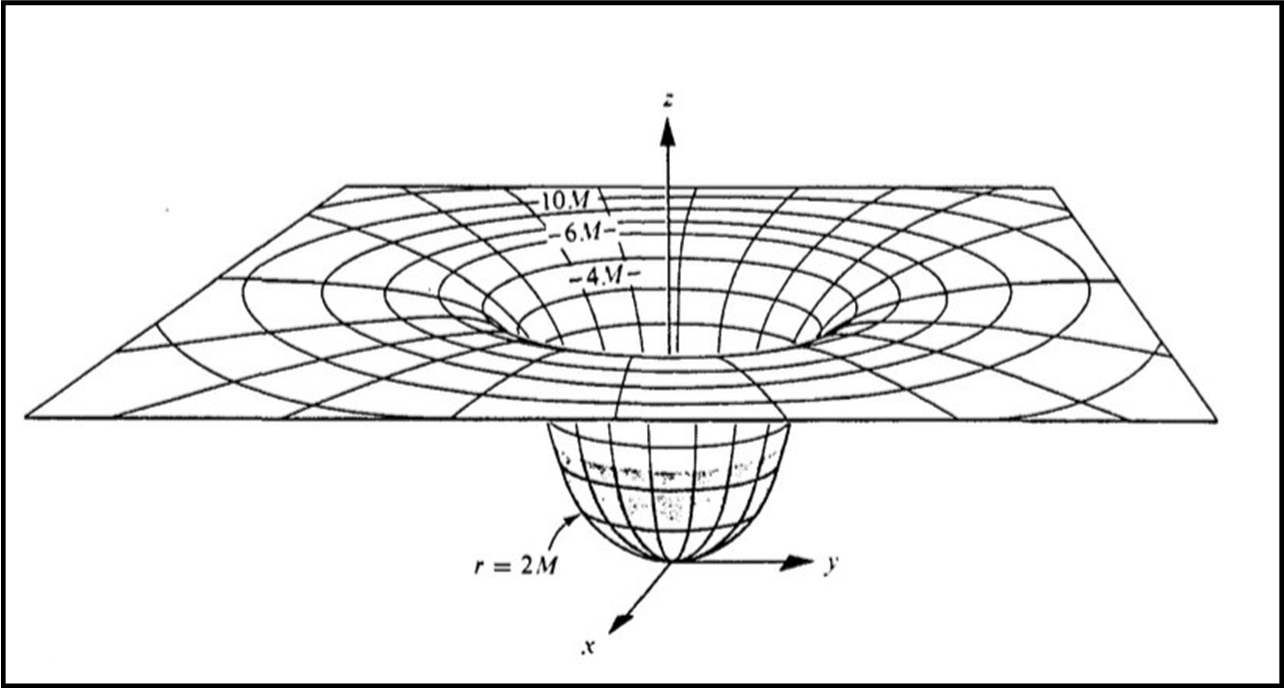
Tuttavia, anche partendo dalle sue conclusioni è possibile saper leggere molto meglio cosa può capitare all’interno del raggio di Schwarzschild, ossia del celeberrimo orizzonte degli eventi. Non è difficile capire che una di queste sfere ha delle caratteristiche peculiari ed è proprio quella che individua il raggio di Schwarzschild.

Per arrivare al nocciolo della questione è meglio ripetere ancora una volta la storia fisica che porta ai buchi neri. Essa sarà di grande aiuto per capire, secondo Einstein e, di conseguenza, Schwarzschild, il vero significato di “singolarità”.

Ciò che la metrica descrive, la Natura esegue (o viceversa …)

Ciò che succede in Natura è che un corpo può mantenere la propria massa, diminuendo il suo raggio (QUI abbiamo ipotizzato cosa accadrebbe all'orbita della Terra se il Sole riducesse il suo raggio fino a diventare un buco nero... la risposta potrebbe sorprendervi!). Questo fatto porta a limiti che non possono essere previsti e descritta dalla fisica newtoniana, ma solo da quella relativistica. Le leggi di gravità che governano l’interno di un corpo estremamente denso sono completamente impensabili per Newton (la trattazione della gravità newtoniana la trovate QUI).

Prima di arrivare al limite estremo, si trovano alcune situazioni intermedie “di sosta”, dove la materia trova uno stato di equilibrio con la pressione esercitata dal collasso gravitazionale. Queste soste intermedie vengono chiamate stati di degenerazione.

Allo stato iniziale la materia è composta da atomi e la prima barriera è quella in cui la pressione viene bilanciata dalle interazioni elettromagnetiche tra atomi, dettata dalla meccanica quantistica. Questi oggetti prendono il nome di nane bianche e rimangono tali fino al ben noto limite di Chandrasekhar.

Superato questo limite (disinteressandosi degli effetti esplosivi della supernova), l’elettromagnetismo non riesce più a opporsi alla pressione. Gli atomi vengono distrutti e la materia normale viene trasformata in qualcosa che può essere chiamata neutronio. In modo molto semplicistico, si ha la produzione di neutroni dalla combinazione di protoni ed elettroni. La materia cambia stato e riesce a riprendere il comando delle operazioni. Siamo nel secondo momento di sosta  e gli oggetti pendono il nome di stelle di neutroni. Ricordiamo che questa fasi sono già state trattate introducendo direttamente la meccanica quantistica e il principio di esclusione Pauli. Adesso, vogliamo solo ricordarle per vedere i vari oggetti che incontra la metrica di Schwarzschild.

La materia, comunque, continua a collassare, diminuendo il raggio della sfera e mantenendo costante la massa. Ed ecco che si ipotizza uno stato di degenerazione del tutto teorico (per adesso). Esso coincide con il limite di  Tolmann-Oppenheimer-Volkoff. Superano questo limite la materia si trasforma in un gas composto da quark e gluoni. Siamo di fronte alle ipotetiche stelle di quark, mai osservate finora.

Va ricordato, ovviamente, che i vari limiti possono essere raggiunti a seconda della massa iniziale. Non tutte le stelle, ad esempio, possono diventare stelle di neutroni.

Niente ci vieta di superare anche questo limite e di aumentare la pressione. A questo punto non esiste nessun meccanismo, nemmeno teorico, che può riuscire a fermare il collasso della materia. Nemmeno la meccanica quantistica riesce, per adesso, a dare il suo contributo. Il corpo continua ormai liberamente il suo collasso fino a che tutta la materia viene contenuta in una regione di spazio infinitesima. Siamo giunti alla singolarità gravitazionale. A questo punto tutte le coordinate di Schwarzschild divergono e le linee geodetiche di Universo sono obbligate a fermarsi.

Siamo giunti al fondo dell’imbuto e non si è più in grado di descrivere i fenomeni che capitano. Singolarità vuol proprio dire incapacità di descrivere la situazione attraverso qualsiasi legge fisica conosciuta. Tuttavia, quando si entra in questo stadio il raggio di Schwarzschild è ormai “esposto”, ossia è esterno alla materia che cade verso la singolarità. Come già detto precedentemente, qualsiasi cosa vi sia all’interno di esso prende il nome di buco nero, anche se, fisicamente, esso dovrebbe essere limitato alla singolarità.

Ricordiamo, ancora una volta, che qualsiasi massa sferica ha un suo raggio di Schwarzschild, ma diventa buco nero solo e soltanto quando la materia è tutta compresa dentro di esso.

Vale la pena di riproporre una figura (Fig. 3) a cui tengo moltissimo, in cui si vede, in un diagramma di Minkowski, l’evoluzione di una stella massiccia che termina la sua esistenza come buco nero.

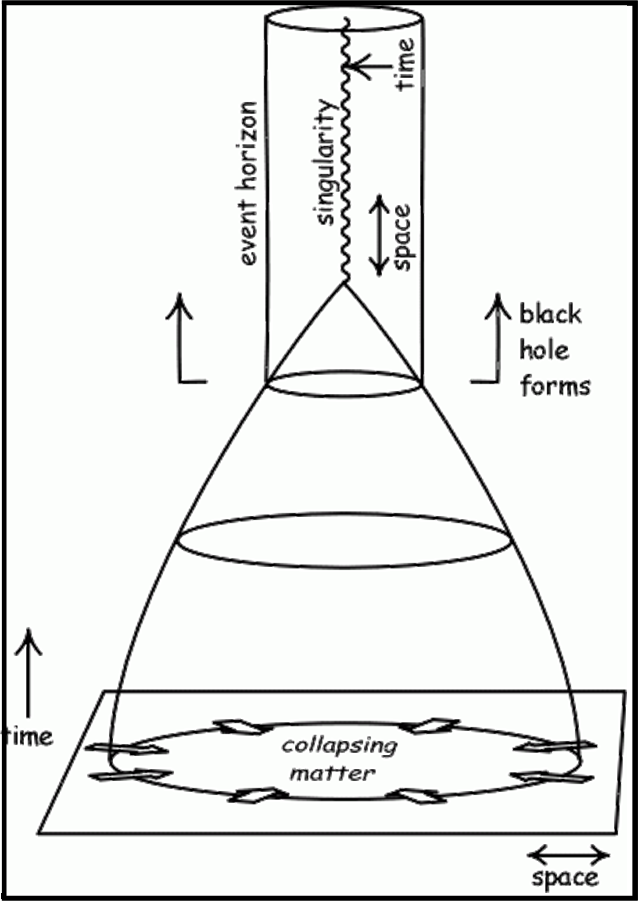
In qualche modo, la metrica di Schwarzschild ci permette di seguire la caduta dall’interno dell’orizzonte fino alla singolarità. Poi qualsiasi approccio deve fermarsi.

Questo è quanto si riesce a fare con la teoria della relatività generale. La teoria, infatti, non può descrivere gli effetti quantistici. La creazione teorica di una singolarità non va considerata come la formazione di un oggetto reale di volume zero e densità infinita, ma come un “errore” legato all’estensione di una teoria oltre i propri limiti di applicabilità. Qualsiasi previsione è quindi priva di senso. La battaglia tra gravità e materia nelle sue estreme condizioni è un qualcosa che la relatività non può affrontare. Per potere andare avanti sarebbe necessaria una teoria unificata, ossia una gravità quantistica, che, sfortunatamente, ancora non esiste.

Tuttavia, anche se impreparata a descrivere una singolarità (per sua stessa definizione), la RG permette, se trattata con la giusta metrica, di descrivere un buco nero come un oggetto macroscopico reale.

Minkowski perde i colpi

Cerchiamo di usare la metrica e lo spazio tempo di Schwarzschild e vediamo a cosa ci può portare.

In qualche modo dobbiamo rifarci alla rappresentazione di Minkowski, ossia ragionare in termini di una struttura causale. Questo significa che non si vuole considerare una semplice “collezione” di eventi, ma attaccare a ognuno di loro il relativo cono di luce, in modo da capire quali sono le possibili traiettorie percorribili da una certa particella che voglia avventurarsi verso un buco nero. Ricordiamo, infatti, se ce ne fosse ancora bisogno, che i coni di luce sono una rappresentazione causale, tale da mostrare quali eventi possano essere connessi causalmente e quali no.

Consideriamo, innanzitutto, uno dei punti chiave dello spaziotempo di Schwarzschild: la gravità piega verso la massa i coni di luce. In poche parole, l’asse del tempo si discosta da quello di un osservatore lontano e si inclina verso l’orizzonte degli eventi.

Un problema non da poco per lo spaziotempo di Minkowski… Noi proviamo lo stesso ad usarlo, piegando i coni di luce, anche se è cosa non “regolare”. Questa operazione poco lecita, ci permette, però, di ricavare in modo molto grossolano (e non privo di errori…) la traiettoria, vista da un sistema in quiete, di una particella che cada verso un buco nero e che prosegua nella sua caduta verso la singolarità

Finché restiamo fuori da lui, il piegamento del cono di luce è tale che è sempre possibile immaginare una traiettoria futura che permetta alla particella di scappare dalla massa che l’attrae, anche se, più vicini si va e più ardua è la fuga.  Giunti sull’orizzonte degli eventi  non vi è più possibilità di uscita, dato che la stessa luce è intrappolata sul raggio di Schwarzschild. Al limite, essa potrebbe stare in quella posizione (in linea di principio), ma non potrebbe uscirne. Nessun evento esterno appartiene al suo cono di luce futuro e quindi non è causalmente connesso alla particella.

All’interno del raggio di Schwarzschild, il cono di luce è talmente piegato che esso punta verso la singolarità. Non solo non è possibile tornare verso l’esterno, ma la strada che si può percorrere è una e una sola: quella verso la singolarità. In particolare, non è più possibile restare fermi.

Il raggio di Schwarzschild diventa un confine molto netto che separa eventi futuri che possono essere causalmente connessi ad altri eventi, da quelli che non hanno più possibilità di scelta: l’unico evento che possono raggiungere è la singolarità. Questa peculiarità del raggio di Schwarzschild (una porta da cui si può solo entrare) fa sì che il raggio di Schwarzschild prenda il nome di orizzonte degli eventi.

La sua definizione più corretta è quindi: una superficie sulla quale i coni di luce sono piegati a tal punto che non può essere percorsa nessuna traiettoria causale futura.

All’interno dell’orizzonte degli eventi si ha un vero e proprio passaggio di consegne tra spazio e tempo. Qualsiasi traiettoria può anche essere rallentata, ma la sua fine porta sicuramente nella singolarità. Le traiettorie tipo spazio avvengono verticalmente, mentre quelle tipo tempo  (casuali) avvengono orizzontalmente.

Vediamo di rappresentare, in modo molto grossolano e anche non corretto, cosa succede lavorando sullo spazio di Minkowski. Un approccio, del tutto personale, che porta con sé gravi inesattezze, ma che, in qualche modo, conforta la vera azione descritta dalla metrica di Schwarzschild.

In Fig. 4, siamo nello spaziotempo di Minkowski e l’orizzonte degli eventi è contrassegnato da due linee verticali che hanno nel punto di mezzo la singolarità.

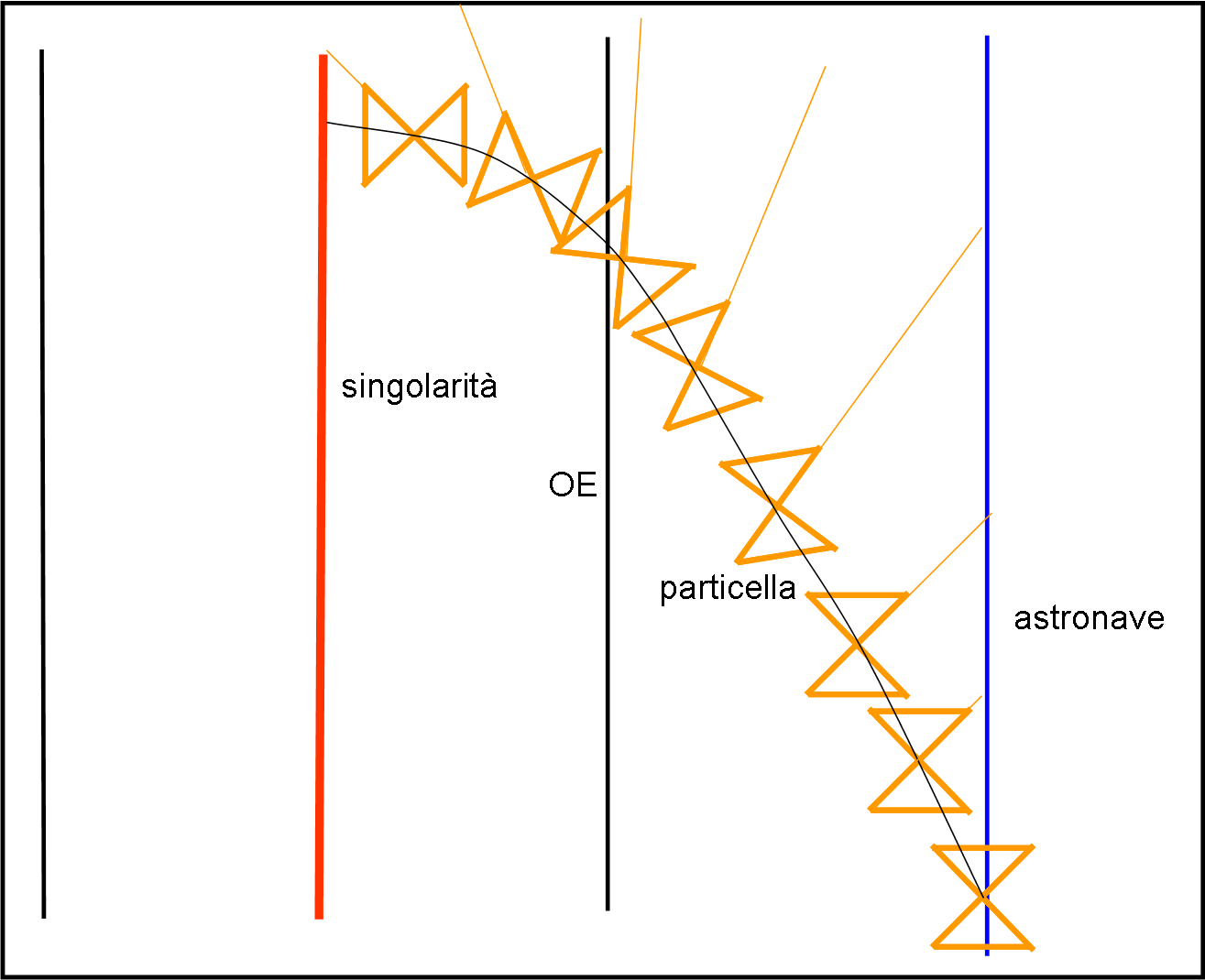
Prendiamo una traiettoria qualsiasi della nostra particella (in qualche modo vista dal suo sistema) e vediamo cosa fa la luce che essa potrebbe emettere a intervalli costanti. In condizioni di riposo assoluto vi è un’astronave che aspetta di ricevere i segnali luminosi periodici dalla particella esploratrice. Fino a che il cono di luce di quest’ultima non è influenzato dalla gravità del buco nero e, quindi, non venga costretta a seguire la metrica di Schwarzschild, i suoi segnali luminosi giungono nel tempo previsto e l’astronave madre può seguire la traiettoria causale della particella (a lei parallela). Poi, piano piano il cono di luce si piega e il segnale luminoso inizia ad arrivare con un ritardo sempre maggiore.

La traiettoria che vede l’astronave madre è un qualcosa che tende ad andare al punto all’infinito della linea che delimita bordo esterno dell’orizzonte degli eventi. In altre parole la traiettoria vista dal sistema in quiete è una curva che tende asintoticamente all’orizzonte degli eventi, come mostrato in Fig. 5. Ciò comporta il ben noto fatto che un osservatore esterno non vedrà mai cadere qualcosa all’interno del buco nero. Essa sembrerà rallentare e fermarsi al suo bordo esterno. Altri effetti, come l’arrossamento della luce, la farà, infine scomparire alla vista.

Portiamoci, adesso all’interno dell’orizzonte degli eventi, dove la nostra particella è realmente entrata senza subire nessun contraccolpo. Il suo cono di luce continua a piegarsi e la sua luce (sempre che abbia senso parlarne) va in verso contrario a prima se vista dalla singolarità. In altre parole sembra che la navicella provenga dall’infinito futuro. Tuttavia, non dimentichiamoci che il vecchio tempo è ormai uno spazio e, quindi, la particella continuerebbe nel suo movimento spaziale da destra verso sinistra, il tutto ribaltato di 90°.

Non voglio complicare ulteriormente le cose che andrebbero viste e spiegate attraverso la metrica utilizzata. Molto meglio, tralasciare visioni un po’ paradossali e rifare la figura nel modo corretto, basato sulla metrica di Schwarzschild, pur accettando dati di fatto altrettanto paradossali.

La Fig. 6  mostra la traiettoria esterna come vista dall’astronave madre e poi quella interna, derivata dalla metrica di Schwarzschild e si può notare come il piegamento dei coni di luce può essere rappresentato da un cambiamento della loro forma.

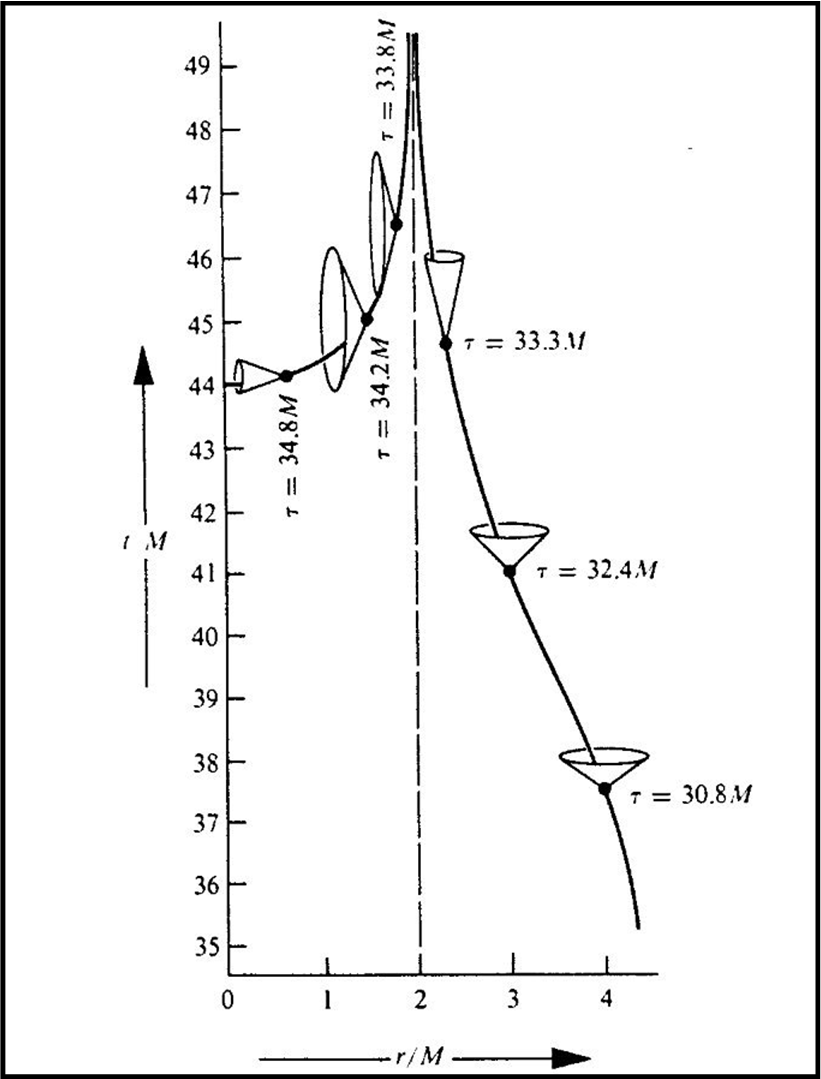
In modo concettuale (non matematico) possiamo dire che la larghezza del cono di luce di un evento è collegata alle sue possibili traiettorie future. Se è largo le possibilità aumentano rispetto al caso di un cono stretto. Evitiamo di andare più a fondo, tralasciando il fatto che gli stessi coni di luce sono più o meno “lunghi”, adottando le classiche coordinate…

Quello che a noi preme sottolineare è che l’orizzonte degli eventi è una singolarità mai raggiungibile per le coordinate di Schwarzschild. In altre parole, questo vuol dire che nessun evento interno è connesso causalmente con un evento esterno futuro.

La Fig. 5 rende il tutto molto più schematico e comprensibile. La particella sale verso l’alto e raggiunge l’orizzonte degli eventi solo all’infinito, così come essa, proviene proprio dall’infinito (attenzione che la linea verticale non è più un tempo, ma uno spazio e che i coni di luce sono estremamente aperti tali da accettare traiettorie che sono ancora causali, come mostrato in Fig. 6).

Tante parole per concludere cosa? Molto semplice: l’utilizzo del diagramma di Minkowski, quando si utilizza la metrica di Schwarzschild, ci trascina verso quei famosi punti che siamo capaci anche di fotografare nella nostra realtà quotidiana (vedi le rotaie di una ferrovia), ma che sono difficili da trattare geometricamente. Stiamo, ovviamente, parlando dei punti all’infinito. D’altra parte ce lo dovevamo aspettare, dato che lo spaziotempo di Minkowski è qualcosa di infinito… Accidenti, proprio la parte più interessante, viene trascinata dove non può essere rappresentata.

E chi l’ha detto? Basta concentrare uno spaziotempo infinito in uno spaziotempo finito, che sia perfino capace di mantenere gli angoli. Cosa possiamo volere di più?

Chi volesse gettarsi sulla metrica di Schwarzschild  abbia solo un po' di pazienza. In un prossimo articolo cercheremo di descriverla in modo ultra semplificato. Penrose può aspettare ancora un po'...

 

In attesa di essere riuniti in un unico approfondimento, QUI trovate tutti gli articoli della serie "Apriamo la porta del buco nero" finora pubblicati