Kepler riesce a misurare la luminosità di una sorgente con una precisione di poche parti su un milione. La variazione di luminosità rivelabile osservata può, perciò, spingersi fino a valori eccezionali che rendono applicabile un metodo mai usato finora. L’applicazione è recente, ma l’idea è molto più antica e risale alla fine del secolo diciannovesimo. Chi l’ha avuta era un ragazzo di sedici anni.

C’è bisogno di dirvi chi è? Penso di no. E’ lui, sempre lui, il grande Albert Einstein! Le sue riflessioni sulla luce inviata da una sorgente in movimento sembra che abbiano dato il via, al suo cervello prodigioso, alla teoria della relatività. Ragione per cui desidero richiamare il concetto generale prima di parlarvi della nuova scoperta e di come la si sia ottenuta. Cercate di seguirlo, perché vi aprirà un mondo inaspettato anche se di una semplicità disarmante. Non farò uso di formule anche se non sarebbe poi estremamente difficile ottenere quella risolutiva. Ci limiteremo a velocità basse rispetto a quella della luce e quindi la parte “relativistica” è appena accennata.

Ciò che Einstein aveva ipotizzato (e come sempre è poi stato confermato) era il fatto che la luce inviata da una sorgente in movimento doveva mostrare un effetto di aberrazione, dato che si doveva tener conto sia della velocità della luce che di quella della stella. Il risultato finale, però, andava ben oltre alla determinazione della direzione finale, ma stabiliva che la luminosità di una stella doveva apparire più intensa se essa si muoveva verso di noi rispetto a quella che avrebbe avuto allontanandosi, e molte altre cose ancora. Il fenomeno, nella sua generalità, portata fino a valori di v comparabili a c, prende il nome di aberrazione relativistica.

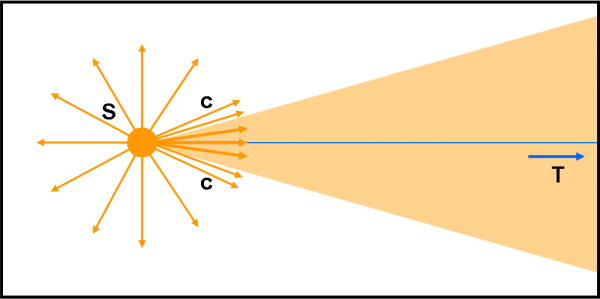
Consideriamo subito la Fig. 3. La stella S manda in giro per l’Universo i suoi fotoni che viaggiano alla velocità c, indicata dai vettori arancioni. Solo una parte di essi ha la direzione giusta per giungere sulla Terra T. Essi sono compresi dentro al cono arancione. Immaginiamo che i fotoni siano solo quelli rappresentati in figura. Solo tre sono interni al cono e, quindi, sono gli unici che il nostro pianeta riesce a vedere.

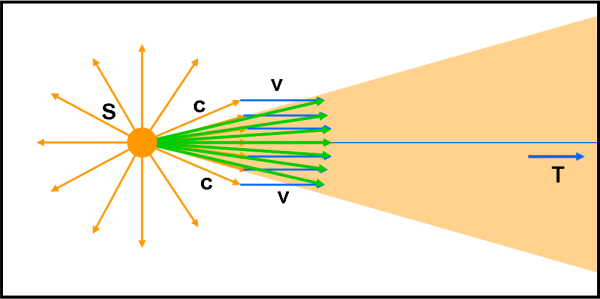
Facciamo adesso muovere la stella in Fig. 4 e, per semplicità, proprio lungo la direzione della Terra. Analoga conclusione avremmo, comunque, anche considerando una direzione diversa. La velocità  della stella è indicata dai vettori azzurri diretti verso di noi. I fotoni sono soggetti a due velocità: quella loro e quella della stella. La velocità risultante si ottiene allora sommando i vettori velocità . Si ottengono i vettori verdi che indicano la direzione dei fotoni. Quanti sono, adesso, quelli che sono contenuti all’interno del cono arancione? Sono saliti addirittura a sette. Cosa significa questa conclusione? Semplice: la luce che riceve la Terra è maggiore di quella ricevuta se la stella fosse ferma. Se avete letto l’articolo precedente non salterete sulla sedia dicendo: “Ma come? Sappiamo benissimo che la velocità della luce non si può sommare ad altre velocità!”. Avreste perfettamente ragione. Ma, noi siamo interessati alla direzione apparente dei fotoni e non all’effettiva velocità che, ovviamente, rimane sempre la stessa, ossia c.

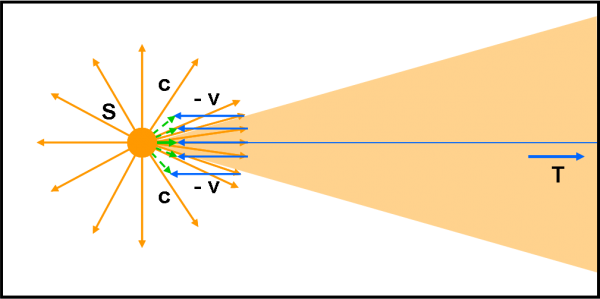
Disegniamo, ora, la Fig. 5. In essa facciamo muovere la stella in direzione opposta con velocità uguale a prima, ossia con velocità –v. I fotoni cambiano, ovviamente, direzione, dato che adesso si muovono lungo la direzione indicata dai vettori verdi che sono la differenza tra c e v o -se preferite- la somma di c e –v. Contiamo quanti vettori verdi sono compresi all’interno del cono arancione. Uno e uno solo. Ciò vuol dire che la luce ricevuta da Terra è inferiore  a quella inviata dalla stella ferma e, a maggior ragione, dalla stella in movimento verso T.

Non ci vuole molto a concludere che se una stella si muove avanti e indietro rispetto alla direzione della Terra la sua luce aumenta e diminuisce periodicamente. Che cosa può fare oscillare in questo modo una stella? Ovviamente, un pianeta che orbita insieme a lei attorno al comune baricentro.

Devo prima, però, fare alcune precisazioni. Ho semplificato di  molto la trattazione limitandomi alla parte più evidente e immediata. In realtà, l’effetto Einstein diventa macroscopico quando la velocità v è confrontabile con c, altrimenti tende a confondersi con l'aberrazione “normale”, che tuttavia è un caso particolare della teoria generale descritta da Albert. Pensate, in particolare, ai getti di materia dai bordi di un buco nero. Lì, veramente, abbiamo v simile a c e non per niente si chiamano getti relativistici.

Se v si avvicina veramente a c non abbiamo soltanto un effetto di intensificazione della luce, ma anche il “restringimento” dell’apparente dimensione della sorgente diventa importante, dato che i raggi sembrano focalizzarsi sempre più verso la direzione del movimento. Qualcosa come quello che si vede nella Fig. 6.

Immaginate, allora, di viaggiare nello spazio a velocità crescente verso la costellazione di Orione (tanto per fare un esempio). Come la vedreste mentre la nave spaziale accelera sempre più? La risposta è data in Fig. 7  (ma guardatela solo dopo averci pensato un po’ sopra) dove il campo di vista resta sempre lo stesso (circa 30°): tutto viene compresso.

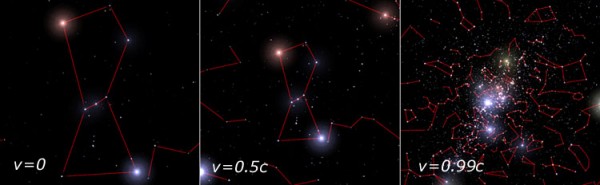
Essa vale  tenendo conto solo dell’aberrazione. Se si tenesse conto anche dell’effetto Doppler le cose si complicherebbero ancora di più… l’Universo in un punto! Non esageriamo, però… (magari ne riparleremo).

Alla prossima e scaldiamo i motori...