Categorie: Fisica classica Strumenti e missioni
Tags: Fizeau frequenza misura velocità luce ruota dentata velocità della luce
Scritto da: Vincenzo Zappalà
Commenti:0
Misurare la velocità della luce. 2: la ruota di Fizeau **
Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO nel quale è stato inserito anche il presente articolo
Dall’esiguo numero di lettori della soluzione del quiz su Archimede e la velocità della luce, temo proprio che la storia sia stata considerata una barzelletta o poco più. In realtà, non è vero, come accennato in qualche risposta e/o commento: il concetto di base è praticamente lo stesso usato da Fizeau nel 1849.
Prima di descrivere l’esperimento torniamo sul punto fondamentale, che Michelson ha risolto con l’interferometria e che Fizeau ha risolto in modo meno raffinato, ma altrettanto geniale. Per calcolare una velocità è necessario conoscere lo spazio percorso e il tempo impiegato a percorrerlo. Su questo dato di fatto c’è poco da fare. Nessun problema per uno spazio a misura d’uomo e la sua misura, ma molti e apparentemente invalicabili quelli riguardanti il tempo.
Utilizzando oggetti molto lontani, come i satelliti di Giove, il tempo diventa una grandezza alla portata di tutti, pur rimanendo molto impreciso. Al limite l’errore più grande proviene dalla conoscenza della distanza dei satelliti di Io ...
Se, invece, si vuole restare sulla Terra ed eseguire tutto in laboratorio o poco più, il “muro” del tempo ci riporta a quanto tentato inutilmente da Galileo. Michelson ha utilizzato una misura indiretta, ossia lo sfasamento dell’onda luminosa in funzione della differenza, anche piccolissima, del cammino ottico. Fizeau ha fatto qualcosa di molto più semplice, ma comunque geniale. Lo scopo finale è, come fatto dal nostro Archy, quello di eliminare l’intervallo di tempo impiegato, ossia trovare un altro fenomeno, che si svolga nello stesso infinitesimo tempo impiegato dalla luce tra andata e ritorno, i cui effetti siano ben visibili e calcolabili.
La ruota dentata di Fizeau
In parole molto povere se non possiamo risolvere la semplice equazione:
c = s/t
basta trovare un’altra velocità tale che
v = d/t
L’importante è che v, s e d siano noti e che t sia lo stesso. Si otterrebbe subito:
t = s/c
t = d/v
s/c = d/v
e infine:
c = s v/d
Come abbiamo visto, Archy aveva usato 4 cavalli alati e due scudi, Fizeau si è limitato a una ruota dentata, estremamente più facile da rifinire perfettamente e far girare a una velocità abbastanza ben determinata.
Raccontiamo il suo esperimento, utilizzando lo schema di Fig. 1.

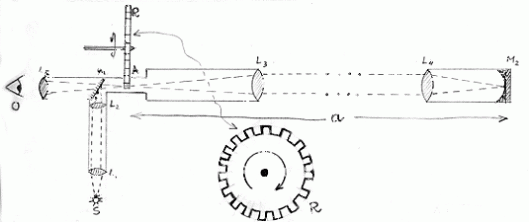
la luce solare (o meglio di una potente lampadina S) viene inviata su uno specchio S1 semitrasparente, inclinato di 45°, che la dirige parzialmente verso uno specchio S2 posto a una distanza d. La luce torna indietro fino ad arrivare all’occhio O di Fizeau attraversando lo specchio S1. Per “maneggiare” al meglio i raggi luminosi vengono usate varie lenti, che possiamo permetterci di trascurare, ma che si possono vedere nello schema originale di Fig. 2.
La cosa veramente importante è inserire una ruota dentata rotante R, attraverso i cui denti la luce è costretta a passare sia all’andata che al ritorno. La velocità della luce è data da:
c = 2d/t
2d è conosciuto, ma non lo è t, il tempo impiegato dalla luce a percorrere il tratto ruota-specchio-ruota ed è impossibile misurarlo direttamente.
La luce inviata verso lo specchio, così come quella di ritorno, viene bloccata o lasciata passare a seconda che si trovi di fronte un dente vuoto o pieno della ruota. All’inizio, a ruota ferma, la si sistema in modo che la luce proveniente da S passi da un vuoto. In tali condizioni O vede la luce al massimo della sua intensità, dopo che ha rimbalzato sullo specchio S2. Poi viene messa in moto. Per velocità angolari ancora basse, la luce riesce ad andare e tornare attraversando lo stesso dente vuoto della ruota. Aumentando la velocità, la luce comincia a diminuire d’intensità, in quanto, al suo ritorno, comincia ad inserirsi il dente pieno. Per una certa velocità, la luce sparisce del tutto, in quanto il dente pieno ha presso esattamente il posto di quello vuoto. Se la ruota girasse ancora più velocemente, si tornerebbe a vedere un po’ di luce fino a che si avrebbe di nuovo un dente “vuoto” e la luce sarebbe nuovamente al massimo della sua luminosità.
Cosa è successo?
La ruota ha n denti pieni, ossia 2n intervalli tra il centro di un dente pieno e il centro di un dente vuoto. Sia ω la velocità angolare della ruota.
Sappiamo che:
ω = 2π/P
dove P è il periodo di rotazione della ruota. In altre parole, uno stesso dente si ritrova esattamente nella posizione originale dopo P secondi. Risulta, quindi, che il tempo necessario per passare da un dente vuoto a uno pieno è uguale a P/2n.
Quando appare il buio completo all’osservatore vuol dire che il tempo P/2n è esattamente uguale al tempo che la luce ha impiegato dal primo passaggio attraverso la ruota al suo ritorno. Il tempo impiegato dalla ruota è facile da calcolare, conoscendo la sua velocità di rotazione. Più facilmente si conoscono i giri al secondo compiuti dalla ruota, ossia la sua frequenza f = 1/P.
Il tempo t, ricavato dalla ruota, è:
t = P/2n = 1/2fn
La formula che dà la velocità della luce diventa, di conseguenza:
c = 2d/t = 4dfn
Fizeau aveva utilizzato:
d = 8.633 km
f = 12.6 giri al secondo
n = 720
da cui:
c = 4 · 8.633 · 12.6 · 720 ≈ 313.000 km/s
Il valore risutò piuttosto alto, dipendendo fortemente dalla misura di f. Nel 1850 Foucalt migliorò la strumentazione e dedusse un valore quasi perfetto (che descriveremo la prossima volta).
E' importante osservare che la velocità della luce così misurata è una media su un tragitto percorso due volte. La cosa era importante ai tempi di Fizeau, dato che si pensava ancora all’etere. Tuttavia, dato che il percorso era di andata e ritorno si poteva supporre che gli effetti della composizione della velocità della luce con quella del vento dell’etere si compensassero. Oggi, ossia dopo Michelson e Morley, sappiamo che la faccenda non aveva alcuna rilevanza.
In attesa che siano riuniti in un unico approfondimento, QUI trovate tutti gli articoli dedicati alla misura della velocità della luce finora pubblicati





