Categorie: Fisica classica
Tags: aereo impazzito forza centrifuga forza di Coriolis moti relativi quiz rotazione e traslazione sistemi inerziali sistemi NON inerziali
Scritto da: Vincenzo Zappalà
Commenti:7
QUIZ (costruttivo) sull'aereo impazzito **
Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.
Eccovi il quiz che ho promesso QUI... Più che un quiz è un invito a lavorare un po' con semplici mezzi che qualsiasi PC (o compasso, righello e matita) possono fornirci facilmente. Il punto chiave è vedere graficamente come agiscono le forze centrifuga e di Coriolis sul moto rettilineo e uniforme di un oggetto (aereo) che vari la sua velocità in rapporto a quella di rotazione della piattaforma da cui parte. Ne vedremo delle belle, soprattutto per velocità lineari molto ridotte...
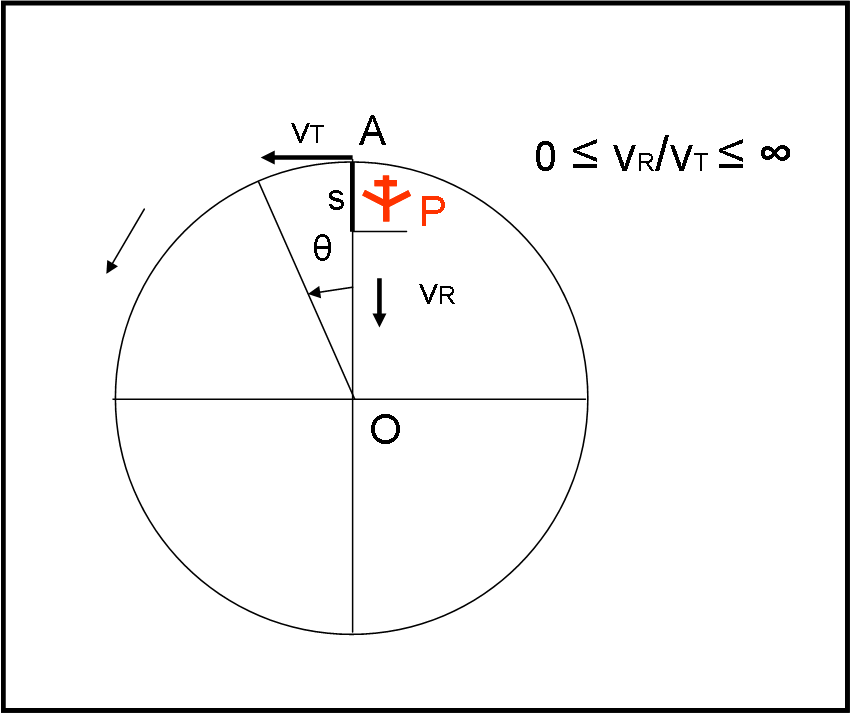
Il rapporto su cui vogliamo lavorare è vR/vT, dove vR è la velocità costante intrinseca (in modulo, direzione e verso) dell'aereo, sollevato dalla sua posizione nella piattaforma rotante (ossia inserito nel sistema inerziale). L'importante è partire con il caso limite, ossia quello in cui la velocità dell'aereo sia ZERO, ossia l'areo sia soltanto spostato in alto in modo da non appartenere più al sistema rotante. Ovviamente non sta fermo, ma si muove seguendo la velocità tangenziale che aveva quando era ancorato al suolo, sulla piattaforma rotante. Siamo perfettamente nel caso della famosa pallina che ruota, tenuta da una corda, quando la si tagli (QUI)
Ovviamente, vogliamo vedere come la traiettoria dell'aereo appare a un osservatore che continui a stare nell'aeroporto... Un po' alla volta, aumentando il rapporto vR/vT , l'aereo sembrerà proprio impazzito soprattutto per valori di vR molto bassi. Poi le cose diventeranno più "normali". Ovviamente si può arrivare al caso in cui il rapporto tende a infinito....
Come già detto precedentemente, potete usare il metodo che preferite (sempre di cambiamento di coordinate si tratta). Beh... buon divertimento (fatevi -magari- aiutare dai più piccoli... il divertimento è assicurato). La prossima volta che vedrete un uragano alla TV lo farete con occhi diversi...
La figura da cui partire è quella che segue... La base di tutto è che nel tempo in cui la piattaforma ruota di un angolo θ, l'aereo P si muove, nel sistema inerziale, di un segmento s, sempre andando nella direzione AO. Il movimento verso O è, però, solo quello dovuto al moto intrinseco dell'aereo. Il punto A è l'aeroporto solidale con la piattaforma.
Qualsiasi animazione sarà ovviamente ben accetta e le migliori saranno inserite nella soluzione.
Una piccola comunicazione: ammetto che la sto facendo molto lunga riguardo ai movimenti relativi. Tuttavia, penso che siano problemi abbastanza semplici da comprendere, ma sui quali molto spesso non si riflette abbastanza, Nell'articolo di approfondimento si potrà anche tagliare qualcosa... vedremo e ... BUON LAVORO!
In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis
7 commenti
Personalmente ho utilizzato il solito metodo, basato sull'impiego del software geogebra. Preciso che geogebra è solo uno strumento , come lo è la matita o il righello. Occorre implementare nel modello la teoria che è alla base del fenomeno, inserendo le equazioni del caso.
Nel mio caso, partendo dalla traiettoria nel S.I., decisamente più facile visto che in esso il moto è rettilineo uniforme con velocità data dalla somma vettoriale tra vr e vt, sono passato alla traiettoria nel S.N.I. con un cambiamento di coordinate. A tale proposito, le equazioni che consentono di passare dal S.I. al S.N.I. (soggetto a sola rotazione attorno all'asse z, stessa origine) sono:
dove x, y sono le coordinate nel S.N.I. e X, Y quelle nel S.I.
Ho, così ottenuto le seguenti traiettorie (in verde quelle nel S.I., in blu quelle nel S.N.I.) per i vari casi.
Caso vr/vt = 0 (praticamente si ha solo la rotazione della piattaforma, nessuna velocità radiale)
Caso intermedio (velocità radiale + velocità tangenziale)
Caso estremo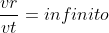
(in questo caso le due traiettorie, nel S.I. e nel S.N.I., coincidono, in quanto praticamente non vi è più rotazione della piattaforma)
Appena definite e se non ci sono svarioni, pubblicherò anche le relative animazioni.
aspettiamo con ansia le animazioni... caro Artù, potresti spiegare meglio cosa rappresenta la farfallina rossa? Ce n'è veramente bisogno? o non basterebbe segnare il raggio di partenza, che è fisso nel SNI e si muove nel SI? In tal modo si evidenzierebbe bene l'angolo alpha... Tutta la mia grafica viene risolta con un semplice passaggio di coordinate (a voi la scelta!).
Grazie Artù
in altre parole, segnare in entrambi i sistemi di riferimento la posizione dell'aeroporto!!!
Quei triangoli rossi al centro, nelle mie intenzioni, servono a evidenziale la rotazione della piattaforma quando ci troviamo nel S.I. Con immagini statiche, in effetti, non servono.
Quella di segnare, al posto dei triangoli rossi centrali, l'aeroporto di partenza può effettivamente essere una valida alternativa. Vedo di affinare la cosa..
Grazie a te per questi continui benefici stimoli alla materia grigia dei lettori, me compreso.
caro Artù,
spero che stimolino, ma ci vogliono persone come te per essere stimolate! Fortunatamente nel nostro Circolo ce ne sono tante!!!! Ovviamente, la soluzione la scriverai tu...
viva la collaborazione! Perfino un giochino alla portata di tutti può inserirci molto bene nel mondo della meccanica anche abbastanza complessa. Coriolis farebbe parte del nostro gruppo, ne sono convinto!!!
Anche tu mi stai stimolando e sto preparando un nuovo piccolo quiz per tutti... Una favoletta per immaginare che ci si può voler bene tra "diversi", anche tra alieni. Il segno del cuore lo capiscono tutti nel nostro Universo.
Va beh... è quasi Natale e cerchiamo di allinearci...
Comunque... grande ARTU', il re della "piattaforma rotonda"
Prendendo spunto dal quiz proposto da Enzo e dall’ultimo disegno di Arturo, mi sorge una riflessione. Considero una ipotetica piattaforma circolare di raggio esattamente uguale a quello equatoriale terrestre e velocità angolare e senso di rotazione esattamente uguali a quelle della Terra, che gira in uno spazio privo di atmosfera e, per semplicità, un ipotetico oggetto, non solidale alla piattaforma, che transita al disopra di essa con direzione il centro di rotazione e con velocità rettilinea uniforme pari alla lunghezza del diametro percorso in 1 h (6.378*2 km / 1h = 12.756 km/h). Dopo 1 ora, un ipotetico osservatore solidale con la piattaforma, vedrebbe la traccia disegnata dall’oggetto deviata di 15° ad est.
Se al posto dell’oggetto, transita un fotone (che provenga dall'esterno del disco e non solidale con questo o che venga sparato da un cannone “sparafotoni” piazzato sul bordo del disco e solidale con questo, non dovrebbe cambiar nulla, nel senso che il modulo di c rimane sempre lo stesso), le cose dovrebbero andare così:
se in 1 h la piattaforma ruota di 15° rispetto all’asse di rotazione, in un secondo ruoterà di 15 / 3600 = 0,00416 (6 periodico) gradi/secondo, ovvero 15’’ di angolo;
il fotone percorre il diametro della piattaforma in 12.756 / 299.792,458 ≈ 0,0425 sec. e l’osservatore sulla piattaforma noterà, al termine del transito del fotone su di essa, una deviazione verso est della traccia disegnata dal fotone pari a 0,0425 * 15 ≈ 0,64 secondi di angolo.
Morale della favola: anche un limite superiore ma finito della velocità, non sfugge al "girevole" abbraccio del moto rotatorio e delle accelerazioni da esso “partorite” (ma solo per i piattaformisti);
solo un’ipotetica velocità in grado di percorrere spazi finiti in tempi nulli ci riuscirebbe.
P.S.
Caro Enzo, cerca di avere clemenza per eventuali "balordaggini" da me scritte.
sai caro Andy... la velocità della luce è quella che è, tuttavia la sua traiettoria risente dei campi accelerati (vedi l'effetto lente). E poi sappiamo che va in linea retta solo nei sistemi inerziali... Un SNI può vedere cose molto strane... La luce permette di giocare con lei... ti ricordi quando abbiamo trattato delle strane visioni degli oggetti in moto relativistico (QUI)...