Categorie: Articoli Curiosità Matematica Riflessioni
Tags: Bach escher Moebius percezioni Topologia
Scritto da: Maurizio Bernardi
Commenti:1
Niente (o quasi) è come sembra
In questo articolo confluiscono, con alcune integrazioni, i contenuti del quiz “Art attack” e dell'articolo “Percezioni illusorie nella visione e nell'arte” presenti in altre sezioni del blog ed è inserito nella sezione d'archivio "Matematica e Geometria".
Niente (o quasi) è come sembra
Gli astronomi, si sa, sono personaggi piuttosto eclettici, ne abbiamo un esempio in casa, anzi, in teatro, il nostro Infinito Teatro del Cosmo.
Così non c'è da stupirsi se uno di loro, August Ferdinand Moebius, (1790 – 1868), oltre a insegnare astronomia nella università di Lipsia, si occupò intensamente di matematica, nel campo della teoria dei numeri e in quello della geometria proiettiva. Ma più che alle sue pubblicazioni astronomiche o alle innovazioni portate nella matematica, la sua notorietà resta legata alla figura topologica che porta il suo nome: una superficie a due dimensioni che, a differenza di un comune piano, come un foglio di carta, non ha fronte e retro, ma una sola faccia.
Se le pagine di un libro fossero scritte su nastri di Moebius ci sarebbero solo pagine dispari.
Una sola faccia e una sola linea di contorno, una conformazione ben diversa da quella di un cilindro, che di facce ne ha due, una interna e una esterna, come ha due linee di contorno (le circonferenze delle sue basi).
Non è certo una esperienza familiare per tutti noi, quella di percorrere lo spazio seguendo un tragitto che presenta torsioni attorno alla linea del moto. O forse si?
Ecco due minuti di video che ci danno la risposta... (si capisce anche togliendo l'audio)
Quante forze fittizie stanno subendo quei simpatici ragazzi… altro che Coriolis!
Ma lasciamo da parte le possibili “applicazioni” e torniamo al concetto implicito nella struttura di questa inconsueta superficie: uno spazio bidimensionale contenuto in uno spazio tridimensionale in cui ciò che conta non sono le misure delle distanze, ma il legame tra i suoi possibili sottoinsiemi, in una parola: la sua forma, la sua “topologia”.
Il significato originale del termine topologia è “studio dei luoghi”, intesi come luoghi geografici; uno studio finalizzato a definire le caratteristiche di un paesaggio. In matematica, assume il significato di studio di quelle proprietà delle figure (forme) che non variano sottoponendole a deformazioni continue (che non provochino rotture, strappi, sovrapposizioni, incollature). Non rientra in questo studio alcuna nozione di misura (lunghezze , aree, ecc). Qualche esempio: un cerchio, da un punto di vista topologico, è equivalente ad un quadrato, pensate ad esempio di modellare la pasta per il panettone in uno stampo quadrato e poi decidere di trasferirla in un contenitore rotondo, più classico, mantenendo la continuità del materiale. Non andrete a creare buchi e quindi nuovi confini, la lunghezza del perimetro e l'area cambieranno perché avete plasmato la materia nella nuova forma, ma non si verrà a perdere la continuità con cui si susseguono i punti della struttura.
Se invece volessimo rimodellare il disco dell'impasto, per formare una “corona circolare”, usando uno stampo per ciambelle, non ci sarebbe alcun modo di riuscirci senza creare un buco, un secondo perimetro “interno”, che cambia la struttura. I due prodotti da forno, ancorché ugualmente squisiti, non sono “equivalenti” da un punto di vista topologico. Prima della lievitazione possiamo pensare che lo spessore sia nullo: avremo un disco e una corona circolare.
Dopo la lievitazione il disco sarà una specie di sfera, diciamo un geoide, e la corona circolare una specie di toro, due soufflé incompatibili, non equivalenti (topologicamente).

Altro esempio: una retta proiettiva (che comprende un punto all'infinito) è equivalente ad una circonferenza, precisamente una circonferenza di raggio infinito, che posso immaginare di contrarre a mio piacimento, riducendola ad un circonferenza di raggio qualsiasi.
Infine, per chiudere con gli esempi: una superficie toroidale è equivalente ad un rettangolo, ma non ad una superficie sferica (che non ha buchi). Vediamo perché:
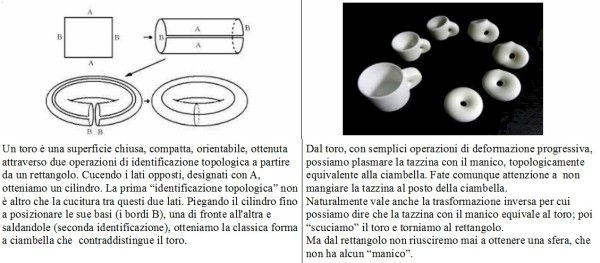
Alcune nozioni di topologia sono abbastanza antiche, basterà ricordare la formula di Eulero, valida per i poliedri topologicamente equivalenti ad una sfera, F-S+V=2. In essa F,S,V sono rispettivamente il numero delle facce, quello degli spigoli, e quello dei vertici di un poliedro. Ma lo studio “consapevole” della topologia inizia solo nel secolo XIX e trae le sue origini da considerazioni svolte in vari tempi, da studiosi impegnati nell'interpretazione di fenomeni fisici (studi di reti elettriche, teoria dei campi elettromagnetici, meccanica celeste).
Senza addentrarci nella teoria di questa affascinante disciplina (chi è interessato a comprendere più a fondo la topologia potrà trovare ulteriori nozioni in questo articolo e in altri che seguiranno), restiamo “in superficie”, ma una superficie alquanto strana, anche nella sua forma più elementare, quella di un nastro avvolto su sé stesso.
Partiamo dalla madre di tutte le strisce e coloriamo una delle sue facce, di verde, lasciando bianca l'altra faccia:

Ora richiudiamo la striscia su se stessa, unendo i suoi estremi con una torsione di 180°, per realizzare il classico "Nastro di Moebius”.
Qui possiamo vedere il Nastro di faccia e di profilo. La sua superficie non è “orientabile” ossia non ha un sopra e un sotto, o un dentro e un fuori, è un tutt'uno.

Ora che lo abbiamo visto, possiamo anche “sentirlo”. La cosa è fattibile e lo potremo constatare tra poco.
Facendo riferimento al Cosmo, ci sono numerose ragioni scientifiche per credere che l'Universo sia un luogo assolutamente silenzioso. Lo spazio è vuoto, ma attraverso le onde radio possiamo sentire gli scoppiettii delle eruzioni solari, le interazioni elettromagnetiche di Giove con la sua luna Io, e persino il battito preciso e regolare delle pulsar. I corpi celesti emettono onde radio che possono essere convertite in suoni. Grazie a questo processo, l'Universo è diventato sonoro, e oggi possiamo sentire anche lo sciabordio delle onde gravitazionali.
Perché non dovremmo poter ascoltare il canto topologico di un nastro di Moebius? La struttura tonale, la specularità, la simmetria, il ritmo, sono elementi fondanti della musica, e un genio come Bach non aveva alcuna difficoltà a manipolare tutto questo, un secolo prima che la topologia venisse chiamata con questo nome. Ascoltiamo...
Interessante, no? Ma torniamo al nastro di carta (a rigore il suo spessore, la sua terza dimensione, dovrebbe essere nulla).
Praticando un taglio longitudinale per tutta la sua lunghezza, otteniamo un nuovo nastro di lunghezza doppia, ma questo ce lo potevamo aspettare, con un po' di intuito. La cosa meno scontata è piuttosto il fatto che ora la torsione della striscia è raddoppiata. Un estremo risulta ruotato di 360° rispetto all'altro.
Questo fatto però non ci riporta nella situazione di un anello privo di qualsiasi torsione. Per meglio dire: la sua superficie ora è “orientabile”, a differenza di quella del Nastro (se proviamo a tracciare su di essa un segno lungo la linea mediana, con la matita, scopriremo che esiste un lato esterno ed un lato interno); tuttavia la torsione ha cambiato qualcosa, si è creato un intreccio che nell'anello piano non esiste.
Ecco il nastro proprio nel momento della scissione, o meglio del raddoppio della lunghezza, un attimo prima di concludere il taglio.

Proviamo a riassestare il nastro in questo modo, semplicemente spostando un lato sopra l'altro...
Nella figura possiamo constatare che nulla è mutato, se non la forma apparente.
Per meglio capire la cosa, vi invitiamo a realizzare fisicamente questo passaggio, vedrete con quale facilità si passa, dall'anello ritorto, alla forma a 8 che appare in questa fotografia.

Qualcuno potrebbe chiedersi cosa accadrebbe se, invece di una torsione di 180°, avessimo eseguito una torsione di 360°, prima di chiudere i lembi della striscia, incollandoli. In particolare, eseguendo il taglio descritto, che risultato avremmo ottenuto.
Ebbene, la prova la potreste fare facilmente da soli, ma vi anticipiamo quello che otterreste...

Un risultato di certo alquanto lontano da quello precedente. C'era da aspettarselo, perché la torsione iniziale di 360° ha dato origine ad una superficie “orientabile” e si vede molto bene come questo fatto agisca sulla generazione dei sottoinsiemi nati dalla scissione del nastro: due anelli concatenati anziché un solo anello di lunghezza doppia. Anche senza alcuna torsione avremmo ottenuto due elementi, ovviamente non concatenati ma disgiunti.
Ma riprendiamo il nostro cammino originale, tornando alla striscia bianca e verde, ora elegantemente avvolta a forma di otto.
Se immaginiamo adesso di disegnare lungo la faccia esterna ( o interna) di questa striscia, la linea mediana e poi di praticare il taglio seguendo il suo tracciato, semplicemente osservando la figura, “vediamo” facilmente , in anticipo, che l'Otto si sdoppierà in due strutture gemelle, con la stessa forma della striscia madre.
Ecco, in concreto, le due strisce gemelle che otteniamo.

Come vedete, anche in questo caso abbiamo colto l'istante della scissione, una separazione effettiva di due individui e non l'allungamento del caso precedente. Ora abbiamo due strisce distinte, gemelle, con la proprietà di sovrapporre perfettamente le loro superfici l'una sull'altra. Vediamolo...

Sembra quasi di poterle estrarre l'una dall'altra e separarle, come possiamo fare nel caso di una striscia priva di qualsiasi torsione, un cilindro che, tagliato a metà, genera due cilindri identici. Invece, no.
Le strisce gemelle che, come le matrioske, si annidano una nell'altra, non sono disgiungibili, ma interlacciate, E se proviamo a separarle, succede questo:

Le strisce sono incatenate tra loro, con una licenza poetica potremmo dire che sono “entangled”, ma forse faremmo rabbrividire il nostro Vincenzo...
Sia la la striscia piana, priva di torsioni, sia la striscia con una torsione di 360°, sono strutture che si riproducono generando ripetutamente figure simili a se stesse.
Continuando gli sdoppiamenti delle nostre strisce, tutto ciò che si otterrà sarà sovrapponibile al precedente passaggio: la larghezza si assottiglierà e lo spessore si ingrosserà ma la forma resterà invariata.
Per analogia possiamo pensare agli anelli generati tagliando la striscia senza torsioni, che possono essere inseriti uno dentro l'altro. Anche in quel caso cambia l'altezza e lo spessore, ma non la forma.
In realtà lo spessore della carta non è nullo, quindi dopo pochi passaggi non sarà possibile proseguire con le successive sovrapposizioni , tuttavia, dal punto di vista concettuale, si tratta di una schiera di "individui" identici che riproducono tutte le caratteristiche del genitore.
Possiamo quindi trarre le seguenti conclusioni:
La striscia di Moebius iniziale contiene una torsione di 180° e presenta una superficie ad una sola faccia.
Dividendosi lungo il percorso perimetrale, si sdoppia generando una striscia che conterrà una torsione doppia (360°) e si svilupperà su una superficie a due facce. Da questo punto in avanti ogni ulteriore scissione genererà sempre una coppia di strisce con identiche caratteristiche, interlacciate tra loro e sovrapponibili.
Il comportamento “anomalo” si manifesta solo nella prima trasformazione, che rappresenta la fase di passaggio dalla configurazione iniziale a quella stabilizzata.
La comprensione di questo meccanismo è stata facilitata dal riassestamento a forma di Otto, che ha reso più “immaginabili” le conseguenze della operazione di suddivisione della striscia da quel punto in poi.
Tutte le suddivisioni del nastro a Otto si sovrappongono, senza fine. Bella raffigurazione intrinseca dell'infinito, anche se la rappresentazione grafica dell'infinito non deriva da questa figura, dato che il simbolo è stato introdotto a metà del 1600 dal matematico inglese John Walllis.

Non a caso, a questo punto, torniamo alla immagine dell'otto-volante, questa volta in una rielaborazione animata di una famosa litografia. E' un otto-volante per formiche, come vedete, frutto del genio di Escher che, attraverso la sua arte, ci comunica profondi concetti matematici.

![]()
Le inattese configurazioni che abbiamo visto scaturire da questa struttura, i raddoppi delle lunghezze, gli anelli concatenati, la ereditarietà delle forme, appaiono quasi il risultato di un gioco di prestigio.
Eppure non c'è nessun trucco e nessuna illusione ottica, solo la conseguenza di avere modellato lo spazio percorso seguendo la torsione della struttura.
Perché lo spazio non è fatto solo per come lo vediamo “di solito”, ma anche per il modo in cui lo attraversiamo e lo osserviamo.
E se non ne siete convinti, eccovi qualche informazione in più...
Il 10 Novembre 1697 nasceva a Londra William Hogart che, nel 1754, realizzò questa provocatoria incisione intitolata “Satira sulla falsa prospettiva”, il cui sottotitolo ammoniva:
“Chiunque disegni senza rispettare le regole della prospettiva potrà incorrere in assurdità come quelle qui illustrate”.
Si noti il poco convincente intreccio delle lenze dei due pescatori, uno in primo piano e l'altro sullo sfondo, o l'enigmatica connessione delle travature che emergono dalle facciate dei due corpi del caseggiato, per non parlare dell'uomo sulla collina che accende la pipa con la fiamma della candela che giace su un piano prospettico assolutamente incoerente.

A ben guardare si potrebbero trovare altri venti e più “errori” sapientemente ed ironicamente dissimulati nella incisione di Hogart.
Le incoerenze nascono da fattori di scala non rispettati e dalla contemporanea presenza di punti di fuga prospettici incompatibili tra loro.
Fino ai primi del '700 la prospettiva veniva insegnata in modo molto approssimativo, le regole matematiche che la sottintendevano erano per lo più ignorate e gli allievi erano incoraggiati ad ispirarsi a dipinti preesistenti di grandi maestri, in modo molto naif. Lo scopo dichiarato di questa incisione, era stimolare lo studio della teoria illustrata in un opuscolo scritto dall'amico di Hogart, Joshua Kirby, che era stato chiamato a sviluppare e diffondere l'approccio rigoroso tra gli allievi della accademia di pittura appositamente fondata dallo stesso Hogart.
Poco più di un secolo e mezzo dopo, il 29 novembre 1915 nasceva a Stoccolma Oscar Reutersvärd, grafico e scultore di fama internazionale. Benché fosse dislessico e avesse difficoltà nella percezione della distanza e della dimensione degli oggetti, venne sostenuto ed incoraggiato nel suo sviluppo artistico dai familiari. Nel 1934, quando aveva solo 18 anni, realizzò una composizione di cubi, disegnandoli in uno spazio tridimensionale a prima vista del tutto “normale”. Tuttavia seguendo l'andamento della struttura l'osservatore ne resta disorientato, come potete constatare in queste immagini.

Ma come dovrebbe essere costruito realmente questo oggetto “assurdo”, per corrispondere alla realtà percepita dai nostri sensi?
Forse così ?

Oppure così...?

Ambedue queste animazioni vi mostrano, semplicemente facendo apparire piccole aree nascoste di un cubo, e nascondendo aree corrispondenti di un altro cubo “apparentemente” adiacente, una dislocazione nello spazio totalmente diversa degli elementi.
Ricorrendo ad una rozza realizzazione pratica, con mezzi modestissimi, si può fisicamente costruire una struttura che si sviluppa su tre assi perpendicolari, come illustrato nella seguente immagine:

Disponendola poi davanti all'obiettivo in modo opportuno, si riesce ad ingannare l'osservatore, creando l'illusione di un congiungimento di assi del tutto irreale.

Naturalmente si vede benissimo che i due cubi intermedi dell'asse che appare in verticale sono sproporzionati rispetto al cubo più in basso, che in realtà è molto più vicino. Ma se, artatamente, sostituissimo quei due cubi intermedi con cubi di opportune dimensioni, otterremmo con facilità una illusione molto più convincente.
E' stato sufficiente applicare questo schema:

Non avete notato che osservando i cubi nelle due animazioni precedenti, dopo un po' vi appaiono come visti dall'interno ( due pareti laterali e un pavimento)? Questa illusione ottica è analoga a quella nota come “cubo di Necker” in cui il cubo, rappresentato in modo ambiguo, può essere visto “da sopra” oppure “da sotto”.
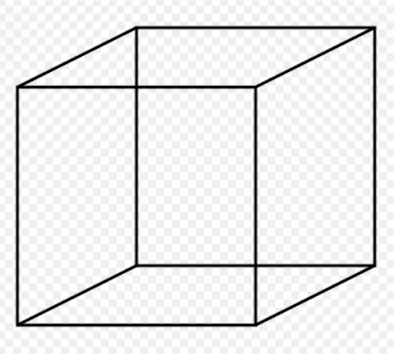
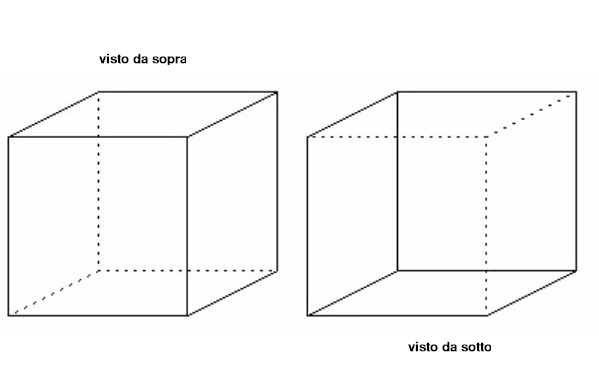
Immagini di questo tipo sono utilizzate anche nei test diagnostici delle lesioni delle aree cerebrali, valutando il numero di “commutazioni” da una visione all'altra che in certi pazienti raggiungono valori di decine al minuto.
Vedere il cubo da dentro e/o da fuori è solo una questione di percezione momentanea, l'ambiguità della figura consente ambedue le interpretazioni. Certo che, se ci sono suggestioni addizionali, i dubbi scompaiono:
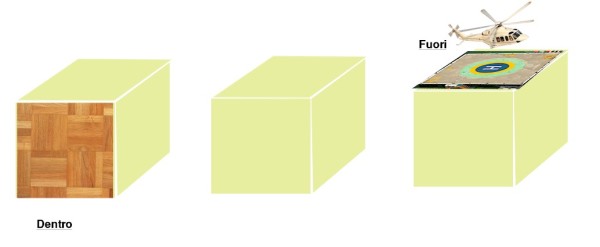
Esiste anche una figura “impossibile” a forma di cubo, raffigurata anche da Escher in una sua opera, intitolata “Belvedere”.
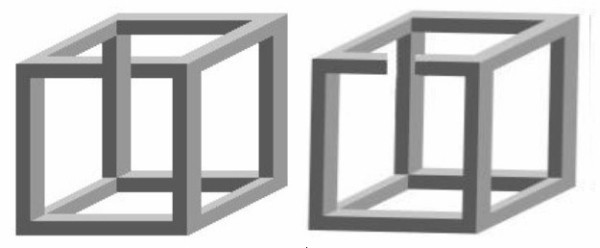
Il cubo è impossibile da realizzare così come si vede, ma si può realizzare una struttura che apparentemente ne ha le peculiarità, come quella disegnata qui sopra, orientandola opportunamente.

Come si può notare nell'angolo in basso a sinistra, la persona seduta sulla panca regge tra le mani un cubo “impossibile” e osserva, sul pavimento, proprio dinnanzi ai sui piedi, un disegno che raffigura la medesima struttura, quasi volesse confrontare disegno e realizzazione tridimensionale.
Questa litografia è del 1958 e riprende molti dei temi cari a Escher, come la scala che si inerpica dal primo al secondo piano con una inclinazione ambigua, o il colonnato e gli archi che sostiene, adagiati su piani prospettici improvvisamente incongruenti. Siamo ben lontani dagli involontari errori dei dilettanti apostrofati da Hogart, siamo tra le abili mani di un prestigiatore che è in grado di farci smarrire il senso del reale, repentinamente, appena il nostro sguardo “volta l'angolo”.
Citiamo, senza ulteriori dettagli, questa pagina di Wikipedia dove compaiono diverse figure impossibili assieme a note illusioni ottiche.
Nel 1926, le splendide incisioni di Escher non contenevano scale impossibili, come in questa “Torre di Babele”, dove la prospettiva, ai limiti dell'aberrazione, è comunque univoca e congruente.

Insomma, i gradini sono gradini e non rebus, il “sopra” il “sotto” e il “di fianco” non si scambiano i ruoli passando da un angolo all'altro del disegno.
Quando, nel 1934, il diciottenne Reutersvärd disegnava i suoi cubi indisciplinati, Mauritius Cornelius Escher, aveva 36 anni ed era già un affermato grafico ed incisore. Le sue opere più famose di quegli anni, raffigurano spazi deformati, riflessi da superfici sferiche, geniali tassellature del piano che trasfigurano in sconcertanti e imprevedibili metamorfosi, temi che torneranno in opere successive, ma è con “Altro Mondo II”, del 1947, che irrompe sulla scena una visione multipla della realtà.
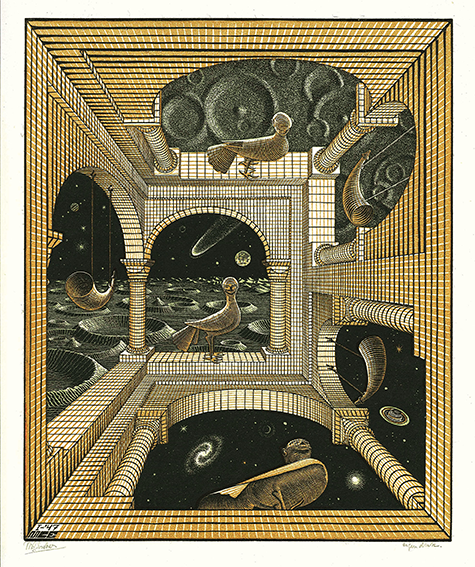
I tre punti di vista sulla scena sono evidenti e correlati, ma non fusi tra loro. L'osservatore li può analizzare in sequenza e farsene un' idea complessiva, come avviene esaminando le viste delle proiezioni ortogonali di un oggetto, informazioni indipendenti, punti di vista complementari che svelano ciascuno una parte dell'informazione totale.
Un cambiamento di registro si avverte l'anno seguente con “su e giù” ove le viste sono incernierate da una specie di ponte che capovolge letteralmente cielo e terra.

Occorreranno però altri cinque anni per arrivare a “Relatività”

La coesistenza di più punti di vista alternativi si esaspera perché Escher introduce la prepotente presenza di figure umane che hanno principalmente lo scopo di testimoniare l'esistenza “chiarificatrice” della gravità. I piedi in terra e la testa in alto, non c'è discussione. Ma la gravità è multipla, coerentemente con la scena. E non solo multipla , ma anche ambivalente, come nel caso delle due figure al centro, in alto, in movimento sulla stessa scala : l'una scendendo, gradino dopo gradino, l'altra salendo, nella stessa direzione, posando i piedi sulla superficie dei gradini “perpendicolare” a quella usata dal compagno.
La geometria della scena, già sconcertante nella sua apparenza statica, diviene del tutto surreale per l'implicita dinamica dei movimenti delle figure umane, che “certificano” la coesistenza di forze di gravità conflittuali.
Qui non si tratta di fondere viste diverse di uno stesso oggetto, bensì di vedere in uno stesso istante tre scene che avrebbero senso in istanti separati. La struttura geometrica, per quanto astrusa è realizzabile, ma la presenza “contemporanea” di tutti i personaggi è irricevibile. Se solo si prova a cancellarne alcuni e lasciare solo quelli coerenti con un singolo centro di gravità, tutto torna normale, o quasi. Poi si cambiano gli attori e, coerentemente, centro di gravità, e la cosa funziona. Quasi una metafora di una società in cui le regole sono relative, diverse a seconda della classe di appartenenza, e coesistenti.
Altre opere analoghe, oltre a “Belvedere” del 1958, sono “salita e discesa”, del 1960

e “la cascata” del 1961

Come in “Salita e discesa”, anche in cascata sono presenti più piani sovrapposti che giustificano la loro esistenza appellandosi al percorso dell'acqua che, notoriamente, scende per effetto della gravità, andando ad alimentare le pale del mulino. Quello che urta contro il comune buonsenso è che subito dopo l'acqua si avvia spontaneamente al piano superiore per ripetere (infinitamente ?) il ciclo. Tutto formalmente perfetto, passo dopo passo, ma sconcertante nel suo insieme, come molti aspetti della vita.
I complici di Escher, nel portare alla luce questi paradossi, sono stati il clima dell'inizio del secolo scorso, portatore di nuove incertezze nell'ambito scientifico, matematico, artistico, come le teorie della nuova fisica, l'evoluzione della matematica, la psicanalisi, eccetera, ma anche il contesto familiare, incline alle materie scientifiche, e la frequentazione di fisici e matematici insigni, come, in particolare, Roger Penrose, nato
il giorno 8 agosto del 1931 a Colchester.
Appartiene anch'egli ad una famiglia che annovera scienziati ed artisti. Insigne cosmologo, fisico, matematico, esperto di intelligenza artificiale, Penrose emerge sullo scenario scientifico in compagnia di personalità come Stephen Hawking. Se consultate gli articoli presenti nel blog, troverete pagine come questa che vi aiuteranno a comprendere la dimensione di questo scienziato.
Ma, a chiusura di questa nostra passeggiata tra le illusioni, vogliamo citarlo semplicemente per l'influenza che ha avuto sull'opera dell'amico di famiglia Escher, con la suggestione del “Triangolo impossibile” alla fine degli anni '50 del secolo scorso, riconoscibile nelle ultime due incisioni che abbiamo visto.

Una figura che Penrose definiva “l'impossibile nella sua forma pura” e di cui possiamo mostrare l'espediente che ne realizza
la parvenza, in questa immagine.

Ci auguriamo, con questo breve articolo, di avere stimolato la vostra curiosità nei riguardi di questi uomini di genio il cui messaggio va ben oltre la ingenua meraviglia per una insolita percezione ottica.
l’Universo tende spesso a illuderci, soprattutto quando qualcosa (anche solo un moto) cerca di eguagliare la caratteristica più peculiare dei fotoni: la velocità… chiedete ad Albert e non solo… Le prospettive e i loro inganni, le distorsioni gravitazionali, i miraggi, le deformazioni dell'informazione, giocano perfidamente con i nostri sensi limitati, ma le nostre protesi tecnologiche ci possono aiutare a superare questo limite, ad estendere le nostre percezioni e, in ultima analisi, a vedere l'invisibile: l'inspiegabile di oggi è destinato a diventare la banalità di domani.
Scarica l'articolo in formato PDF






1 commento
Non posso non dirlo: questo articolo è veramente splendido per vari motivi, sia intellettuali che pratici. Lo legherei molto bene (e non c'è da stupirsi) all'approfondimento sulle visioni relativistiche e sulla stessa aberrazione. Ciò dimostra che quando si cerca di ampliare la visione scientifica, non si può che sconfinare nella visione artistica e in quella filosofica (vedi Giordano Bruno) e in molte altre manifestazioni diverse dello stesso organo: la mente.
Scusate... ma sono veramente fiero dei miei colleghi circolari che stanno permettendo questo fondamentale allargamento di visione dell'Universo. Ancora una volta prende vigore la frase di Feynman: l'Universo in un bicchiere di vino. Noi possiamo permetterci di dire l'Universo (quello vero, quello completo) nelle pagine di un piccolo circolo e nelle persone che lo alimentano con la forza della mente.
Lo so, lo so, è un commento che non dovrei fare proprio io, ma sapete che vado sempre in direzione ostinata e contraria...