Categorie: Fenomeni astronomici Fisica classica
Tags: anticicloni atmosfera binari ferroviari caduta dei gravi cicloni forza di Coriolis gravità sistema rotante Terra
Scritto da: Vincenzo Zappalà
Commenti:0
Gira, il mondo gira: la forza di Coriolis. 7: Arrivano i cicloni! **
Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.
Vediamo di concludere la nostra lunga trattazione sulla forza di Coriolis, abbandonando palline, astronavi, aerei e, perfino, pendoli. La nostra piattaforma rotante è diventata tutta la Terra e vogliamo studiare, in modo molto divulgativo, l’effetto più vistoso della forza di Coriolis (e di sua sorella centrifuga). Stiamo parlando dei vortici ciclonici e anticiclonici. I primi, soprattutto, causano i celebri cicloni con i loro effetti devastanti. Purtroppo, la forza di Coriolis ha un peso non indifferente sulla creazione di questi tragici fenomeni atmosferici.
Cerchiamo di spiegare come ciò può avvenire, facendo tesoro di quanto abbiamo imparato finora.
In Fig. 1 possiamo disegnare la superficie terrestre e localizzarci su una fascia intermedia, tropicale.
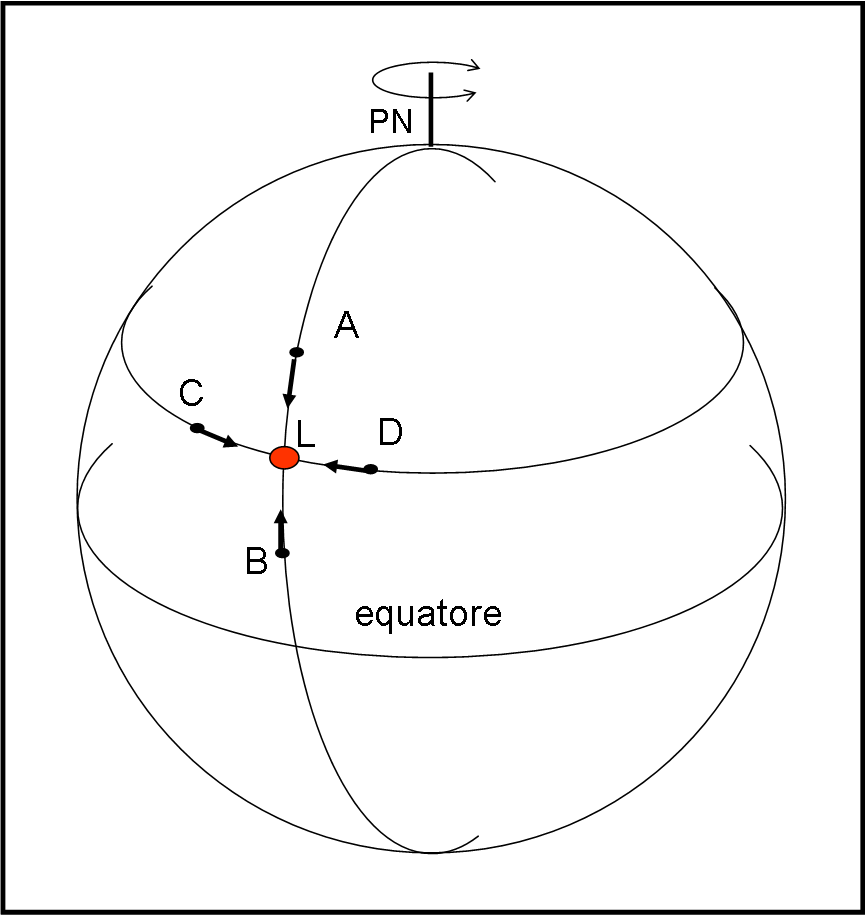
Seguiamo il viaggio di quattro particelle o di goccioline d’acqua. Esse ruotano solidalmente con la Terra, se non vi sono forze esterne a modificarne il moto. Immaginiamo, adesso, che in un certo punto dell’emisfero nord terrestre vi sia un centro L di bassa pressione. Non voglio certo inserirmi negli studi del nostro amico farfallino, perciò mi limito a dire che le quattro particelle si “staccano” dal legame terrestre e iniziano a muoversi senza attrito (in prima approssimazione) verso la depressione. Possiamo dire che esse vengono spinte dal vento. A noi, meccanici puri, questa situazione ci dice soltanto che vi sono quattro palline che si stanno muovendo su un sistema rotante.
Per capire meglio la situazione guardiamo la Terra dal Polo Nord (Fig. 2).
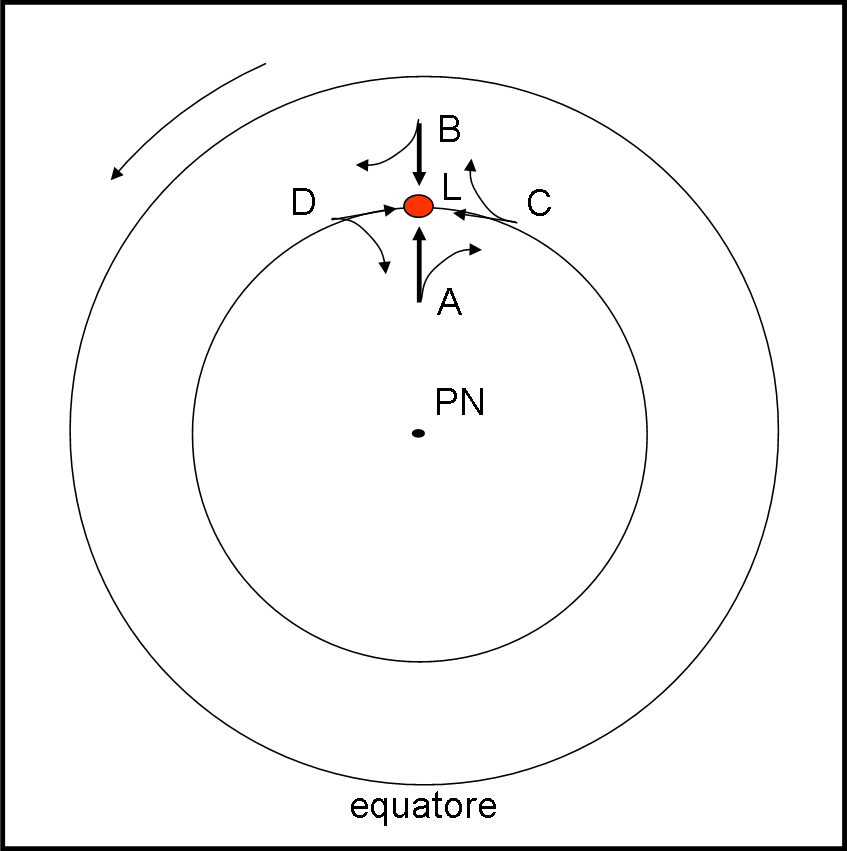
E’ facile notare che la particella A sta scendendo verso l’equatore (ossia verso il bordo esterno della nostra ben nota piattaforma girevole), mentre la particella B sta salendo verso il Polo Nord. I nostri grafici (e le nostre poche formule) ci dicono subito cosa vedrebbe un osservatore nel sistema terrestre rotante: esso vedrebbe piegare misteriosamente le due particelle, entrambe verso destra rispetto alla direzione del moto. La colpa, per lui è dell’accelerazione di Coriolis e di quella centrifuga. Ovviamente, la stessa cosa deve succedere per un osservatore inerziale (il solito alieno in visita). Per lui non è molto difficile spiegare il tutto con le leggi di Newton. La particella che parte dal basso conserva la velocità tangenziale di rotazione che si somma a quella verticale, da cui nasce la curva che vede percorrere dalla particella B. Analogamente vede la particella A che si stacca dal sistema rotante con un velocità tangenziale molto piccola (addirittura nulla se partisse dal polo). La conclusione è comunque la stessa: la particella percorre una curva spostata verso destra rispetto al moto ventoso. In fondo è ciò che abbiamo notato e studiato parlando di astronavi e aerei e anche del pendolo di Foucault.
In molti testi ci si ferma qui, dato che le due tracce curvilinee, con tanto di freccia, fanno già pensare a una rotazione delle particelle in senso antiorario (nell’emisfero nord). Tracciando linee ventose più o meno inclinate rispetto al centro depressionario la struttura assumerebbe sempre meglio la tipica forma del ciclone. Già a questo punto si possono dire due cose ovvie: se invece di un centro depressionario, vi fosse un centro di alta pressione, le particelle scapperebbero in direzione radiale e la rotazione finale sarebbe di tipo orario. Esattamente il contrario capiterebbe nell’emisfero meridionale.
Facciamo ancora notare, sempre che ce ne sia bisogno, che il vortice si vede sia nel sistema rotante che nel sistema inerziale (come nel pendolo di Foucault). Infatti il fenomeno fisico deve essere lo stesso e le particelle che si muovono lasciano un chiaro segno sulla superficie terrestre così come faceva la polvere nel pendolo mosso dal nostro orso bianco (tra parentesi continua a stare molto bene, anche se si sta lamentando un pochino del freddo… sapete, è un fautore del GW…).
Tuttavia, pur restando a un livello estremamente semplificato, e ricordando che entra in gioco la gravità terreste, possiamo ancora migliorare la forma del nostro vortice ciclonico. Facciamo passare un parallelo attraverso il centro depressionario. A questo punto consideriamo le particelle C e D che si muovono proprio lungo il parallelo. La particella C sta andando più veloce di un punto stazionario sulla Terra e quindi tende a “decollare” ossia a portarsi più in alto, avendo una forza centripeta maggiore. Tuttavia, la gravità terrestre non le permette certo di uscire impunemente dall’atmosfera e allora la nostra particella deve cercare una posizione che competa alla velocità acquisita. La cosa migliore da fare è spostarsi verso l’equatore (ossia verso destra) in modo da vivere in pace con la sua velocità maggiorata. Il processo contrario capita per la particella D che va in senso contrario al moto terrestre. Essa è costretta a diminuire la sua velocità e tenderebbe ad andare verso il suolo. Tuttavia, una soluzione molto più “fisica” e semplice è quella di spostarsi verso una zona dove la sua velocità è quella “normale”. Essa si sposta verso latitudini maggiori, dove la velocità è minore. In altra parole, ancora verso destra e il vortice si realizza perfettamente, come possiamo notare bene nella Fig. 3. A sinistra un vortice costruito tenendo conto anche di altri fattori legati all’atmosfera, a destra un vero ciclone tropicale.
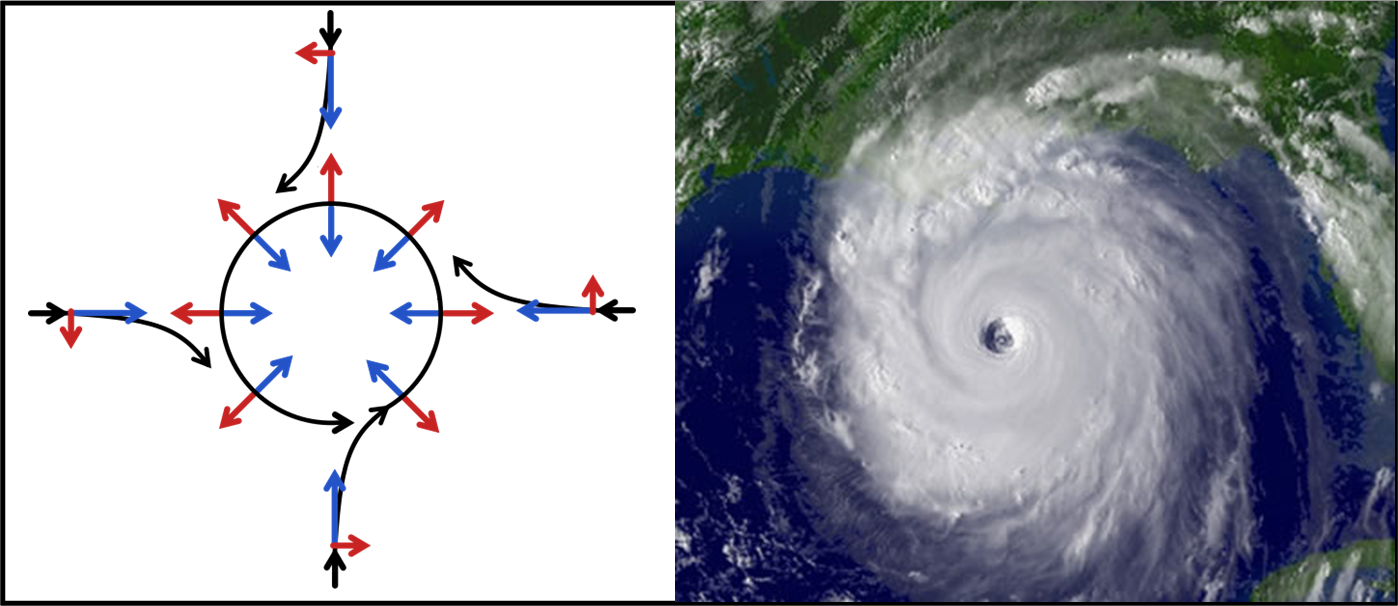
Possiamo fin da subito concludere con una notizia un po’ triste (ma non ditelo ai grandi degustatori di vino): per ottenere strutture così vistose e impressionanti sono necessari venti e tempi decisamente notevoli. Niente di tutto ciò può quindi avvenire negli scarichi dei lavandini (o in un bicchiere di vino…)! La rotazione dell’acqua dipende dalla forma e dalle condizioni di partenza. Inoltre, essendo un fenomeno che attira molto i turisti, spesso si costruiscono scarichi adatti allo scopo e si impara facilmente a versare l’acqua nel modo … giusto.
Prima di terminare, dobbiamo ricordare ancora qualche effetto della nostra forza così misteriosa e così semplice e attiva.
Il primo è quello relativo alla caduta dei gravi che ha permesso a Guglielmini di provare (anche se lasciando parecchi dubbi) la rotazione della Terra 60 anni prima di Coriolis. Per saperne di più basta andare a leggere questo divertente e istruttivo articolo di Maurizio. In poche parole, il discorso è sempre lo stesso: un oggetto viene lasciato cadere da una torre molto alta e si trova in caduta libera. Tuttavia, mantiene la velocità tangenziale che aveva a quell’altezza. Scendendo si porta ad altezze alle quali corrispondono velocità sempre minori. Quando arriva a Terra si troverà spostato verso est, in quanto la sua velocità originale che si è conservata gli ha permesso di anticipare la rotazione del suolo terrestre. Una spiegazione più che sufficiente. Tuttavia, ricordiamoci che un corpo in caduta libera, nel sistema di riferimento terrestre, subisce anche la forza di Coriolis (movimento da una zona esterna della piattaforma rotante verso il centro). Ne segue che l’interpretazione corretta dell’esperimento di Guglielmini è ben più complessa di quanto possa sembrare.
Più immediato è l’effetto sulle rotaie di un treno… Se una tratta Nord-Sud (o Sud-Nord) viene percorsa sempre nella stessa direzione, il binario di destra sarà più consumato, in quanto la forza di Coriolis tende costantemente a deviare il treno verso destra.
Analogamente, provate a camminare su un tram mentre sta girando. Se gira a sinistra vi sentirete sbattere verso destra. Così come capiterebbe su una città spaziale rotante.
In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis





