QUIZ: un ottagono "russo" **** (NEW: inserito suggerimento)
Per i più esperti, ecco un bel quiz di origine russa (e i russi ci sanno fare). Vi sono probabilmente diversi metodi per arrivare alla soluzione. Io ne ho trovata una che mi sembra carina. A voi la sfida...
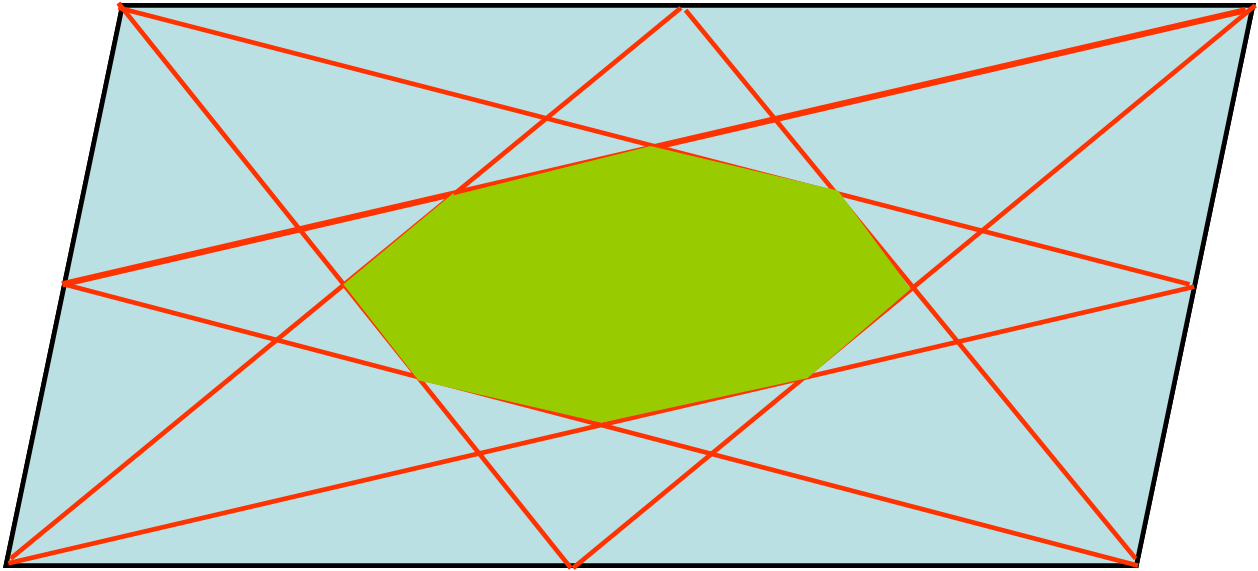
Consideriamo un parallelogramma qualsiasi. Da ogni vertice mandiamo la congiungente ai punti di mezzo dei lati non contenenti il vertice. Si ottiene la simpatica figura che segue. La domanda è molto semplice: "Qual è il rapporto tra l'area dell'intero parallelogramma e quella dell'ottagono verde che viene costruito automaticamente".
Ovviamente, nessuna formula trigonometrica...
SUGGERIMENTO:
bisogna considerare/dimostrare come le linee costruttive che, intersecandosi, danno i vertici dell'ottagono, determinano una precisa suddivisione delle lunghezze dei lati.
Non abbiate perciò paura a dividere la figura in parti più piccole, dato che molte uguaglianze si ripetono... Vale la pena provarci e limitare il raggio d'azione a un sottoinsieme della figura...
Soluzione QUI
30 commenti
Considero un quadrato di lato "l"
Costruisco l'ottagono secondo le istruzioni - il centro è "O"
Limito l'analisi al quarto superiore sinistro ( lati in rosso)
I punti di intersezione A C B sono vertici dell'ottagono.
AO = BO = CO = l/4 = raggio del cerchio circoscritto all'ottagono
area di OACB = CD*CE +1/2*CE*EB + 1/2 AD*CD
area OACB&space;+&space;(l/4&space;-&space;l/(4*\sqrt{2}))*&space;l/(4*\sqrt{2}))
AREA OTTAGONO = 4* area OACB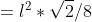
rapporto AREA OTTAGONO/ AREA QUADRATO =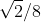
(circa 17,6 %)
Questo rapporto ( e il suo inverso, richiesto nel quiz) si conserva (spero) deformando il quadrato in un parallelogramma.
Abbi pazienza... ma almeno fai un rettangolo. Il cerchio circoscritto sparisce....
Ma, poi, il bello è trovarlo per un parallelogramma qualsiasi... non facilitiamo troppo le cose.... (comunque il risultato non è giusto... dovrebbe venire un numero intero (AQ/AO))
Un piccolo aiuto per trovare l'errore...
attenzione alla costruzione di un ottagono regolare...
A parte il valore del risultato e la soddisfazione di ragionare su un parallelogramma generico e sui vari triangoli nella figura, è sbagliato fare questo ragionamento?
Nel quadrato di lato 4 unità ho 16 unità di misura di superficie, di forma quadrata. Il cerchio verde occupa un certo numero di queste unità.
Se riduco della metà l'altezza del quadrato ottenendo un rettangolo, le singole caselle subiscono la medesima trasformazione e diventano unità "rettangolari" di misura della superficie.
Corrispondentemente il cerchio si trasforma in una ellisse, ma il numero di caselle che occupa non cambia. Quindi neppure il rapporto tra area della figura (ellisse) e area del rettangolo che la contiene cambierà.
La figura è questa.
Se il ragionamento non è sbagliato, dovrebbe valere anche passando dal rettangolo ad un parallelogramma generico.
va bene ti concedo di lavorare con un quadrato, ma senza fare errori...
A occhio, l'area dell'ottagono mi sembra metà della metà della metà dell'area del parallelogramma
caro Andy... a volte l'occhio non basta
Maurizio era partito bene, ma poi si è perso dietro un ottagono che non è regolare e quindi niente cerchio....
Grazie, Vincenzo, ora ci riprovo...
Questa è la figura un cui scelgo come parallelogramma un quadrato.
L'area dell'ottagono è quindi =^{2}&space;*&space;2\sqrt{2&space;})
=
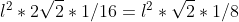
L'area del quadrato è =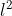
il rapporto tra area del quadrato e area dell'ottagono è =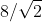
(però non mi viene un numero intero...)
Vedo ora il commento dell 15.46 ( mentre stavo preparando il disegno)
Allora, se l'ottagono non è regolare, si spiega tutto... la sua area non è quella che ho calcolato.
Caro Maurizio... l'ottagono non è regolare per come viene costruito e non esiste un cerchio circoscritto... Ti avevo fatto la fig. poco sopra. D'altra parte, se passi al rettangolo, le cose cambiano e hai un'ellisse....e non valgono più le tue relazioni. E, invece, tutto deve restare uguale...il rapporto finale non cambia.
In ogni caso, CD non è uguale a CE
Il rapporto vale 6. Resta solo da dimostrarlo...
Ehi, il solo , va inteso tra virgolette... "solo"
Se l'ottagono fosse regolare, non viene fuori il quadrato di partenza...
Come fai a dire che vale 6 ?
Io ti consiglierei di lavorare almeno con un rettangolo, in modo che certe lunghezze risultino chiaramente diverse le une dalle altre. Il quadrato può ingannare più facilmente....
Il suggerimento di passare ad un rettangolo è certo valido ma vorrei arrivare a concludere il mio ragionamento sul quadrato: cioè, adesso il mio quiz è diventato questo... abbi ancora un po' di pazienza.
A me sembra che l'ottagono, pur non essendo regolare, (ha angoli diversi, come giustamente hai evidenziato con il tuo disegno) abbia comunque tutti i lati uguali.
Ecco la figura su cui ragionerò:
In particolare AB = BC
Per costruzione so che CD/BD =1/2 e AE/BE = 1/2
L'area di AEB vale quanto quella di BDC e l'area del quadrato bianco vale 4 volte la stessa area AEB
Complessivamente l'area OABC vale 6 volte l'area AEB. Ho così espresso l'area di 1/4 dell'ottagono.
Estendendo a tutti i quadranti il ragionamento l'area complessiva dell'ottagono non regolare ma di lati uguali, vale 24 unità AEB
Calcolo l'area AEB in funzione del lato del quadrato...
Il segmento OA vale un quarto del lato l cioè OA=l/4
AE vale un terzo di OA: AE= l/12
EB vale due terzi di OA: EB= l/6
l'area AEB vale 1/2 * l^2 * 1/72 = l^2 /144
moltiplico per 24 e ho l'area dell'ottagono
Area ottagono = l^2 * 24/144 = l^2* 1/6
Area totale quadrato = l^2
Rapporto tra area quadrato e area ottagono = 6
Per il ragionamento esposto in un precedente commento questo rapporto resta costante deformando il quadrato in un rettangolo o in un generico parallelogramma.
Sono sicuro che la tua soluzione segua una logica diversa ma, come dicevi, ci possono essere soluzioni alternative e per questo ho cercato di portare a conclusione questa. Spero di non avere commesso altri errori.
Per rispondere alla tua domanda "come fai a dire che il risultato è 6"... Semplicemente, dato che avevi detto che il risultato era un numero intero, ho dedotto che fosse il numero più vicino alla mia precedente risposta (sbagliata, ma numericamente non di molto) Detto in numeri il mio calcolo portava rapporto tra AO/AT = 0,176 molto vicino al rapporto 1/6= 0,166. Quindi, dovendo trovare un numero intero...
caro Mau,
Direi che mi sembra corretto (e alternativo). Tuttavia, mi piacerebbe che provassi direttamente a provarlo su un rettangolo. Dato che non esiste più il cerchio circoscritto, dovrebbe funzionare senza bisogno di fare l'estrapolazione. Il metodo che ho seguito io non dipende assolutamente dalla scelta dl parallelogramma e penso che debba succedere anche con quanto hai esposto tu...
Forza ragazzi! Ci sono sicuramente altri metodi più o meno rapidi e più o meno eleganti... Vi do un piccolo AIUTINO:
bisogna considerare/dimostrare come le linee costruttive, che intersecandosi danno i vertici dell'ottagono, determinano una precisa suddivisione delle lunghezze dei lati.
Non abbiate perciò paura a dividere la figura in parti più piccole, dato che molte uguaglianze si ripetono... Vale la pena provarci e limitare il raggio d'azione a un sotto insieme della figura...
ok. ci provo io.
il rapporto è sempre 1/12
si vede bene geometricamente.
no. mi scuso ho letto male. il rapporto tra l'area del parallelogramma e l'ottagono è 6. avevo fatto i calcoli su metà
per la dimostrazione io allego questa.
ho calcolato l'area del trapezio arancione, e del triangolo giallo.
l'area del trapezio arancione, se l e h sono il lato e l'alteza del parallelogramma, vale sempre (l/2+l/3)*(h/12)
mentre quella del triagolo giallo vale (l/3)*(h/12)*(1/2)
sommandole e moltiplicando per 2 si ottine l*h/6
quindi ne consegue che il rapporto tra area del tra area del parallegromma (l*h) e l'area dell'ottagono (l*h/6) è 6
Bene, bene Shedir... Però sarebbe bello dimostrare velocemente perché valgono certe uguaglianze (base, altezza del trapezio e del triangolo... l/3 e h/6... sono piccolezze, ma per completezza... ). Comunque il problema sta diventando sempre più semplice ... bravi, bravi. Vi posso dire che era stato considerato "very hard" in Russia... Dai, forza... il nostro Circolo e i suoi lettori rendono tutto più semplice del previsto
In realtà (con il secondo di Mau che non ha inserito ufficialmente) penso che la vostra soluzione sia meglio della mia... Che bello!!!!
C'è qualcuno che riesce a fare ancora meglio? (non credo, ma chissà...)
Guardando meglio... penso che il metodo di Shedir sia il più veloce possibile, tuttavia è necessario dimostrare che i vari segmenti siano proprio quello che appaiono nelle formule, ossia: l/2, l/3 e h/12. Non è così banale....
Forza, ancora un piccolo sforzo!
Complimenti a Shedir per la linearità e l'eleganza della impostazione. Per facilitare le dimostrazioni richieste da Enzo ai lettori del quiz, inserisco questa immagine (la stessa di Shedir) con alcune quote significative.
Evidente, ad esempio la dimostrazione del valore h/4, e quella di l/2.
Meno immediato, ma non difficile, dimostrare il perché di l/3 e della suddivisione di h/4 in due parti rispettivamente di 1/3 e di 2/3.
Per trovare le relazioni tra i vari segmenti potrebbe essere utile entrare nel piano cartesiano e scrivere equazioni di rette e fare intersezioni...
Mi accorgo che nel mio metodo questo problema non si pone... Forse, forse, non era così male...
Per risolvere il quiz io ho utilizzato alcune considerazioni di simmetria e la proporzionalità tra le altezze di triangoli simili. Allego la figura e dopo spiego il ragionamento.
Indico con a la base AC del parallelogramma e con h la sua altezza.
Trattandosi di parallelogramma e di punti medi, l'area dell'ottagono risultante posso calcolare sommando le aree dei tre triangoli colorati in figura, PLI, LKI e KIJ, e moltiplicando il risultato per due.
Cominciamo con l'are adi PLI:
PL=a/2
Devo calcolare l'altezza, pari a KQ. Considero a questo fine i due triangoli BPH e KLH. Essi sono simili (rette parallele tagliate dalla stessa trasversale, angolo in comune etc...). Dunque (proporzionalità tra le altezze di due triangoli simili):
PH:LH=BR:KQ
Ora, LH=a/4. Infatti, dalla figura si vede subito che PL=a/2 e , per simmetria, FP=LH. Poichè FH=a, deve allora essere 2LH=FH-PL=a-a/2=a/2 e quindi LH=a/4. Quindi, PH=PL+LH=a/2+a/4=3 a/4. Infine, BR=h/2. Dunque, dalla proporzionalità suddetta, si ricava:
KQ=BR*LH/PH=h/6
Posso ora calcolare l'area di PLI=1/2 x a/2 x h/6 = ah/24
Passiamo ora al triangolo LKI. L'altezza di questo triangolo la conosco già: KQ=h/6. Mi manca la base KI. Considero i triangoli IGK e AGC. Essi sono simili. Quindi (proporzionalità tra altezze di triangoli simili):
AC:KI=h:(h-h/6)
da cui:
KI=AC / 3 = a/3
Quindi, l'area di LKI è = 1/2 x a/3 x h/6 = ah/36
Passiamo infine al triangolo KIJ. La base la conosco già: KI=a/3. Per calcolare l'altezza JV:
JV=JS-KQ
JS=h/4 (da immediate considerazioni geometriche) quindi:
JV=h/4-h/6=h/12
Quindi, l'area di LIJ è= 1/2 x a/3 x h/12 = ah/72
L'area del semiottagono è quindi:
ah/24 + ah/36 + ah/72 = ah/12
l'area dell'ottagono, allora, sarà 2 ah/12 = ah/6
Essendo l'area del parallelogramma pari a ah, facendo il rapporto ottengo infine:
ah/(ah/6) = 6
scusate, chi volesse ingrandire la figura la trova qui:
http://www.infinitoteatrodelcosmo.it/wp-content/uploads/2018/01/cattura.jpg
E bravo Artù che è riuscito a trovare il tempo per il nostro quiz!!!!
metodo un po' lungo, forse, ma decisamente diverso... ne uscirà fuori un intero volume di soluzioni!!!!
Nessuno, però, si è ancora avvicinato alla mia... vi posso dire che ho preso un sottoinsieme ancora più piccolo, dove i triangoli simili diventano immediati... "il peso sulla Luna è la metà della metà... selene ene ah...."
Traggo spunto dalle soluzioni ottimamente esposte da chi mi ha preceduto e dai suggerimenti di Enzo, per proporre la mia soluzione, aiutato da un amico fidato: il cerchio
.
In questi disegni, sequenzialmente, la mia soluzione al quiz:
https://i.imgur.com/5yM7SRH.jpg
https://i.imgur.com/2kY5YSb.jpg
https://i.imgur.com/pmEgLky.jpg
Ottimo Andy... ti aspettavo al varco!!!!!