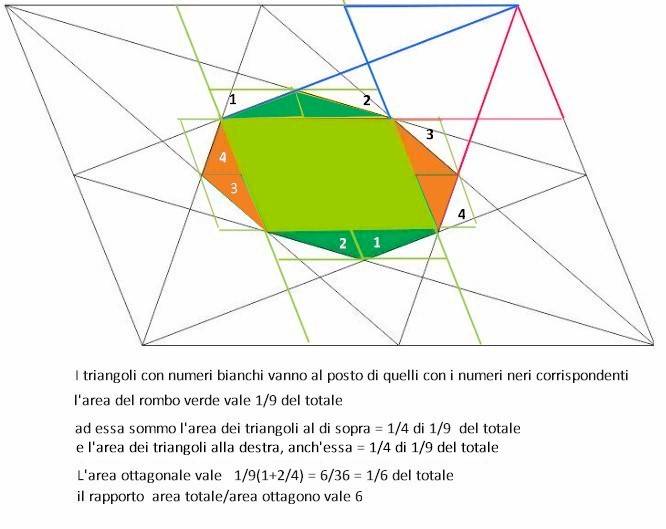
Categorie: Matematica
Tags: aree geometri ottagono parallelogramma quiz soluzione
Scritto da: Vincenzo Zappalà
Commenti:0
Soluzione(i) dell’ottagono e del parallelogramma ***
Un quiz che presenta svariate soluzioni e che è stato affrontato e risolto con grande passione da almeno quattro lettori (di cui due "maghi"). Vale la pena inserire le loro strategie operative direttamente nella soluzione, ringraziando Maurizio e Scherzy per avermi aiutato in quest’opera di compattamento. Alla fine, ho aggiunto anche la soluzione scelta da me e che segue una trattazione abbastanza diversa.
Prima di passare al calcolo delle aree, è bene mettere in evidenza come la scelta dei lati della figura comporti molti triangoli simili e la possibilità di calcolare varie lunghezze in funzione sia del lato maggiore che minore del parallelogramma. I metodi usati da Maurizio, Shedir e Arturo hanno bisogno di questa parte preliminare. La stessa cosa sarà di molto semplificata nel metodo scelto da me. Andiamo avanti con molta calma e attenzione
Primo metodo (Maurizio)
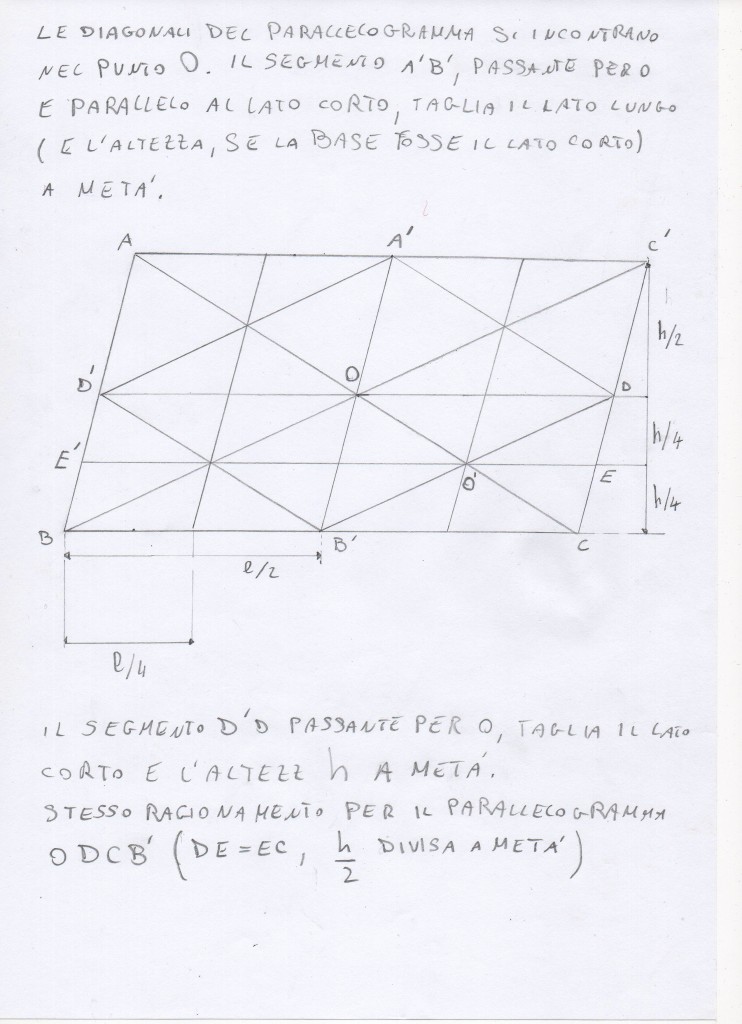
In Fig. 1, divido il parallelogramma, di lati a e b ,(il cui centro è O ) in 4 quadranti e considero uno solo di essi: OEBC
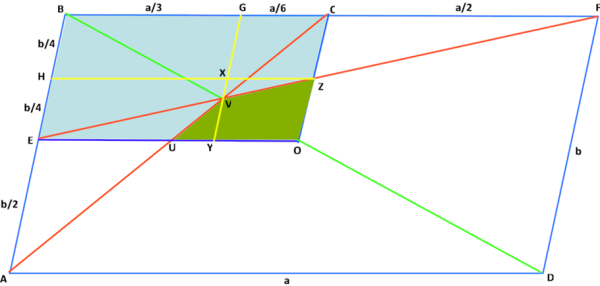
La linea AC congiunge il vertice A con il punto intermedio del lato orizzontale opposto C
La linea EF congiunge il punto intermedio E del lato obliquo al vertice F
L'intersezione di queste due linee V è un vertice del quadrato. I due vertici adiacenti a V, U e Z sono le intersezione di AC e EF con le linee mediane OE e OC.
Traccio la diagonale (verde) BD e considero i due triangoli AVD e CVB. Essi sono simili (in modo evidente) e i loro rispettivi lati stanno nel rapporto 1:2 Pertanto, sulla diagonale, il segmento BV vale 2 VD e quindi BV è 1/3 della intera diagonale. Proiettando il punto V sul lato orizzontale BF, secondo una linea (gialla) parallela al lato obliquo, trovo il punto Y sulla linea mediana e il punto G sul lato orizzontale, tale che BG = a/3
Poiché BC = a/2 si deriva immediatamente GC = a/2-a/3 = a/6
L'intersezione di EF con la linea mediana CO individua Z. E'immediato dedurre che le due distanze OZ e CZ sono uguali.
Traccio la linea orizzontale (gialla) passante per Z e individuo H sul lato obliquo
Le due linee gialle ZH e GY si intersecano nel punto X.
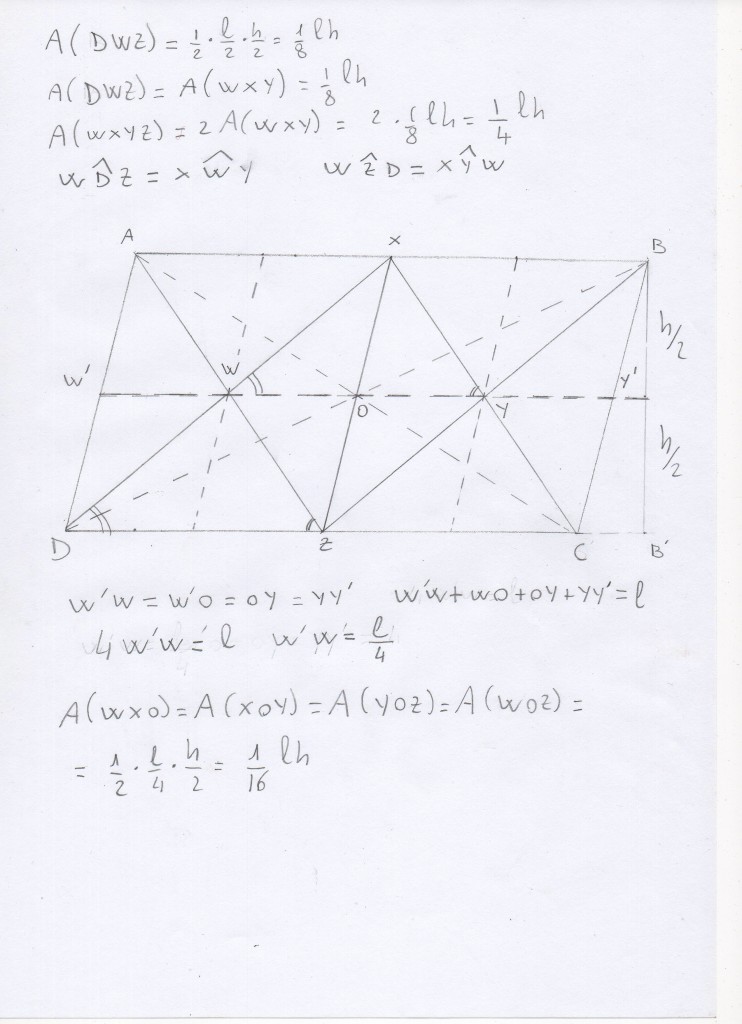
Ora devo dimostrare che i due triangoli UYV e VXZ hanno la stessa area.
UY = UO-YO = a/4 - a/6 = a/12 analogamente:
XV = GV-OZ = b/3 - b/4 = b/12
XZ = GC = a/6
VY = XY-Xv = b/4 - b/12 = b/6
le aree dei due triangoli sono identiche ( = k*ab/72 dove k è funzione dalla inclinazione del lato obliquo).
Posso quindi scambiare il colore di questi due triangoli, come nella Fig. 2 seguente, in cui aggiungo una linea gialla obliqua che divide a metà AGBY formando 4 parallelogrammi identici a OYXZ.
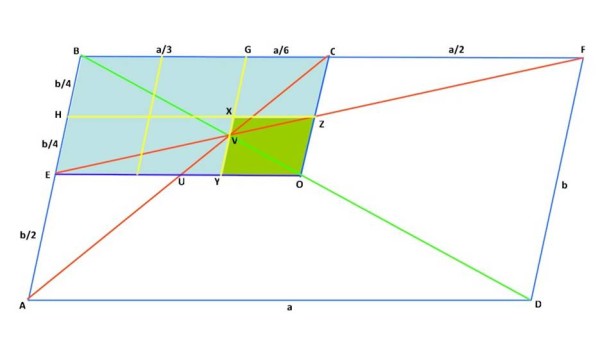
Dei 6 parallelogrammi (identici) che appaiono nella figura, quello verde concentra la superficie dell'ottagono.
Il rapporto cercato è quindi 6 e vale, ovviamente, estendendo il risultato a tutta la figura.
Versione alternativa di Maurizio
La soluzione consiste di queste due figure.
La prima dimostra la suddivisione dei lati in proporzione a 1/3 e 2/3 ottenuta con le linee di costruzione dell'ottagono.
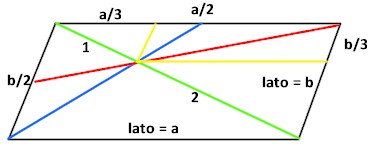
Per la similitudine dei due triangoli con basi a (lato orizzontale in basso) e a/2 (lato orizzontale in alto), la diagonale verde è divisa in due segmenti, di cui uno ( 2) lungo il doppio dell'altro ( 1) .
Le proiezioni del punto di intersezione (verde-blu) sul lati del parallelogramma rispecchiano questa ripartizione.
La seconda figura illustra come si ottiene il risultato richiesto.
Si notino le coppie di triangoli simili contornati in colore blu e violetto per meglio comprendere le proporzionalità su cui si basano i calcoli.
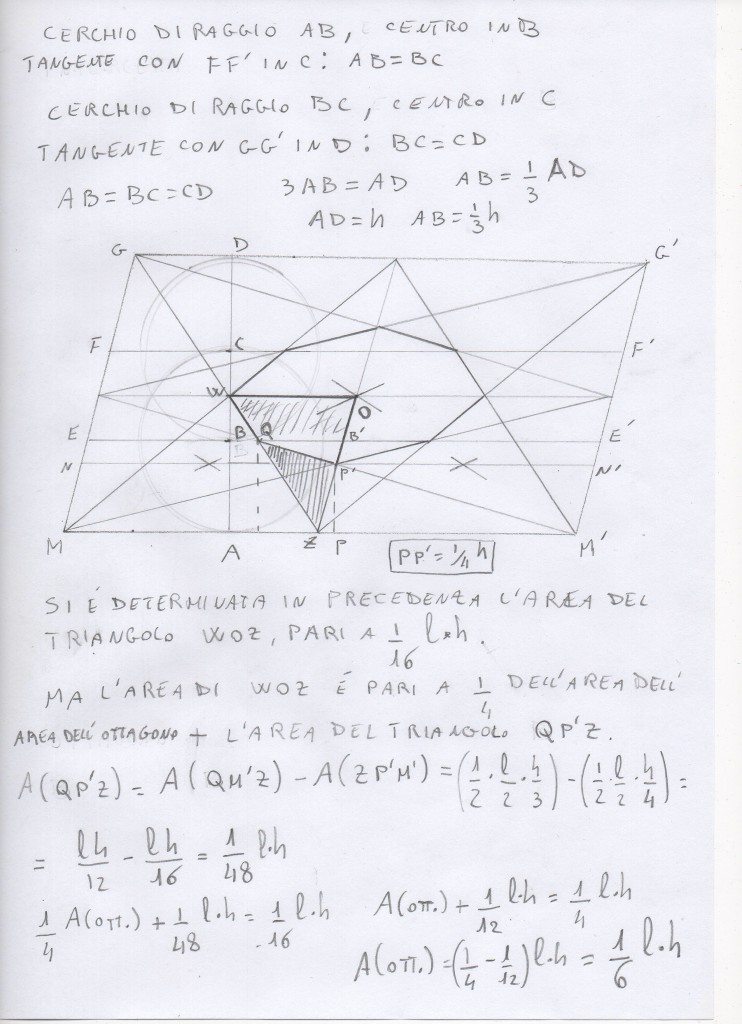
Secondo metodo (Shedir)
La figura su cui ragionare è la Fig. 3:
Per facilitare la lettura delle formule che appaiono nel seguito, può essere utile riportare alcune “misure”, che derivano dai medesimi ragionamenti già esposti nella descrizione precedente (primo metodo) in una figura (Fig. 4) corredata delle opportune “quote”.
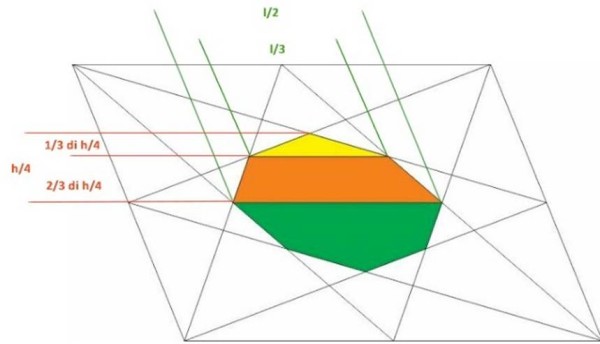
Ho calcolato l'area del trapezio arancione, e del triangolo giallo.
l'area del trapezio arancione, se l e h sono il lato e l'altezza del parallelogramma, vale sempre (l/2+l/3)*(h/12)
mentre quella del triangolo giallo vale (l/3)*(h/12)*(1/2)
sommandole e moltiplicando per 2 si ottiene l*h/6
quindi ne consegue che il rapporto tra area del tra area del parallelogramma (l*h) e l'area dell'ottagono (l*h/6) è 6
Terzo metodo (Arturo)
Per risolvere il quiz io ho utilizzato alcune considerazioni di simmetria e la proporzionalità tra le altezze di triangoli simili. Allego la Fig. 5.
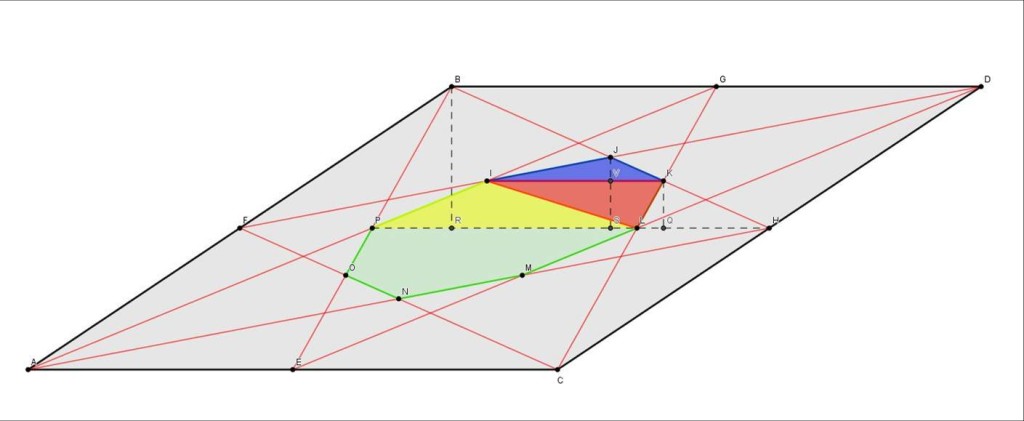
Indico con a la base AC del parallelogramma e con h la sua altezza.
Trattandosi di parallelogramma e di punti medi, l'area dell'ottagono risultante la posso calcolare sommando le aree dei tre triangoli colorati in figura, PLI, LKI e KIJ, e moltiplicando il risultato per due.
Cominciamo con l'area di PLI:
PL=a/2
Devo calcolare l'altezza, pari a KQ. Considero a questo fine i due triangoli BPH e KLH. Essi sono simili (rette parallele tagliate dalla stessa trasversale, angolo in comune etc...).
Dunque (proporzionalità tra le altezze di due triangoli simili):
PH:LH=BR:KQ
Ora, LH=a/4. Infatti, dalla figura si vede subito che PL=a/2 e , per simmetria, FP=LH. Poichè FH=a, deve allora essere 2LH=FH-PL=a-a/2=a/2 e quindi LH=a/4.
Quindi, PH=PL+LH=a/2+a/4=3 a/4. Infine, BR=h/2.
Dunque, dalla proporzionalità suddetta, si ricava:
KQ=BR*LH/PH=h/6
Posso ora calcolare l'area di PLI=1/2 x a/2 x h/6 = ah/24
Passiamo ora al triangolo LKI. L'altezza di questo triangolo la conosco già: KQ=h/6. Mi manca la base KI. Considero i triangoli IGK e AGC. Essi sono simili. Quindi (proporzionalità tra altezze di triangoli simili):
AC:KI=h:(h-h/6)
da cui:
KI=AC / 3 = a/3
Quindi, l'area di LKI è = 1/2 x a/3 x h/6 = ah/36
Passiamo infine al triangolo KIJ. La base la conosco già: KI=a/3. Per calcolare l'altezza JV:
JV=JS-KQ
JS=h/4 (da immediate considerazioni geometriche) quindi:
JV=h/4-h/6=h/12
Quindi, l'area di LIJ è= 1/2 x a/3 x h/12 = ah/72
L'area del semiottagono è quindi:
ah/24 + ah/36 + ah/72 = ah/12
l'area dell'ottagono, allora, sarà 2 ah/12 = ah/6
Essendo l'area del parallelogramma pari ad ah, facendo il rapporto ottengo infine: ah/(ah/6) = 6
Quarto metodo (Andy)
Questa soluzione ve la proponiamo “as it is”, conservando il look “Leonardesco” con cui l'autore l'ha proposta. Carta e matita... un segno indelebile di chi usa ancora la testa ( si può usare anche con il PC, ma chi sceglie carta e matita è una garanzia)! Bravo Andy!
Quinto metodo (Vincenzo)
Io ho usato il metodo di Modugno relativo al peso sulla Luna (sbagliato!): la metà della metà. Ho continuato a dividere a metà il parallelogramma fino a ottenere la Fig. 6 e puntare tutto sul parallelogramma grigio.
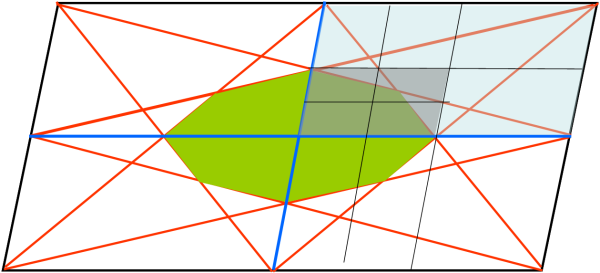
Esso vale 1/16 dell’area totale del parallelogramma di base AP. La parte di ottagono compresa in questo piccolo parallelogramma è ovviamente solo 1/4 dell’area dell’ottagono di base AO
Dividiamolo ancora in 4 parti uguali e mettiamo un po’ di lettere (ma non ce ne sarebbe nemmeno bisogno) come mostrato in Fig. 7.
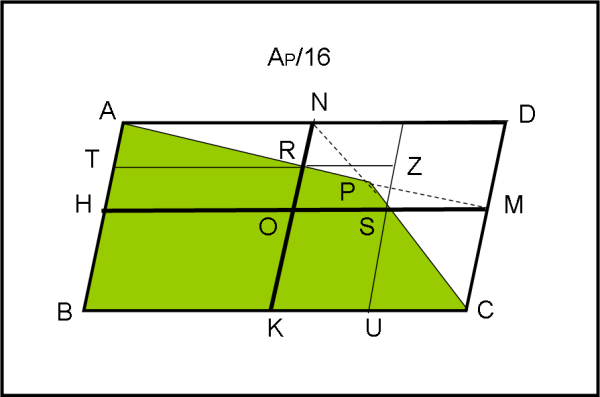
Proprio per avere lavorato alla Modugno è immediato concludere (per costruzione) che:
triangolo ATR = triangolo OMR = triangolo ARN
triangolo SUC = triangolo SON = triangolo SMC
Scriviamo qualche numero…
Area parallelogramma HOKB = 1/64 AP …. (1)
Aerea trapezio AHOR = 3/4 AHON = 3/4·1/64 AP …. (2)
Area trapezio OKCS =3/4 OKCM = 3/4 ·1/64 AP …. (3)
Non ci rimane che calcolare l’area del quadrangolo RPOS. Basta usare ancora Modugno e dividere in quattro parti uguali il parallelogramma NODM. Accidenti! Ma questo parallelogramma non è altro che 1/16 (1/4·1/4) del parallelogramma ABCD. Ne segue (ci vuol poco a dimostrarlo, avendo sempre dimezzato) che anche la parte dell’ottagono RPSO risulta 1/16 di ABCP. Ossia:
Area quadrangolo RPSO = 1/16 1/4 AO = 1/64 AO …. (4)
La somma di (1),(2),(3),(4) non è altro che 1/4 AO
Basta scriverla:
(1/64) AP + (6/4) (1/64) AP + (1/64)AO = (1/4) AO
(4 + 6)/(4· 64) AP = (64 – 4) (4· 64) AO
AP/AO = 60/10 = 6
Tanto per cambiare…
A voi la scelta…
Il Quiz lo trovate QUI