Categorie: Astronomia Elementare Matematica
Tags: cicloide epicicli ipocicli ipocicloide quiz Tolomeo
Scritto da: Maurizio Bernardi
Commenti:0
Soluzione dei quiz sulle monete che rotolano
Unendo le forze, Andy, Arturo e Maurizio hanno messo insieme questa soluzione dei due quiz (QUI e QUA - QUO non c'è, è andato a fare una passeggiata) sulle monete rotolanti (The rolling coins), quasi una cronaca di un giorno da "facce da schiaffi"...
Nei commenti al primo quiz avrete notato l'esplicito riferimento fatto da Vincenzo alla “rulletta”, una curva avvolta da un tenebroso mistero. Ecco la descrizione che Blaise Pascal (1623-1662) fa della roulette, nella Histoire de la roulette:
La roulette è una curva talmente comune, che, dopo la retta e la circonferenza, essa è quella più frequente; ed è spesso sotto gli occhi di tutti, tanto che c'è da stupirsi che non sia stata studiata dagli antichi, che non hanno tralasciato nulla al riguardo. La roulette, infatti, non è altro che il percorso che fa nell'aria il punto di una ruota, quando essa rotola nel suo movimento normale, dal momento in cui il punto comincia a sollevarsi da terra, fino al momento in cui la rotazione continua della ruota l'abbia ricondotta a terra, dopo un giro completo; supposto che la ruota sia un cerchio perfetto, il punto preso in esame sia un punto della circonferenza, e la terra sia perfettamente piana.
Storicamente, di essa non v’è traccia nella geometria classica; in questo senso può essere considerata una curva “nuova”, uno dei primi frutti cioè della rifioritura della Matematica nel XVII secolo, e studiata da tutti i matematici di quel secolo. Difficile dire chi per primo l’abbia considerata. Certamente la studiò Nicola Cusano (1401-1464) nei suoi tentativi di “quadratura del cerchio” e Mersenne (1588-1648) la definì rigorosamente stabilendone la prima ovvia proprietà, che la lunghezza della sua base è pari alla circonferenza generatrice. Cercò quindi di trovare l’area sotto la curva senza riuscirvi. Galileo le diede il nome Cicloide (nel 1599) e cercò anche di misurarla teoricamente, senza però riuscirvi. Ecco cosa scrive in una lettera a Bonaventura Cavalieri:
Quella linea arcuata sono più di cinquant'anni che mi venne in mente il descriverla, e l'ammirai per una curvità graziosissima per adattarla agli archi di un ponte. Feci sopra di essa , e sopra lo spazio da lei e dalla sua corda compreso, diversi tentativi per dimostrare qualche passione, e parvemi da principio che tale spazio potesse essere triplo del cerchio che le descrive; ma non fu così, benché la differenza non sia molta.
Da buon fisico qual era, in realtà, si era ingegnato a ritagliarla da superfici di noto peso specifico, sperando così di trovarne l’area attraverso il peso della parte ritagliata; trovò così che il rapporto dei pesi con il cerchio generatore era di circa 3 a 1, ma decise che non era esattamente 3 ma probabilmente un numero irrazionale molto prossimo. Evidentemente la soluzione 3 gli era apparsa incredibilmente semplice.
Ma la sfida era ormai lanciata e in due, indipendentemente l’uno dall’ altro, riuscirono a dimostrare che l’area sotto la curva era esattamente tre volte quella del cerchio generatore. Uno dei due fu Roberval che lo risolse nel 1634; l’altro fu Evangelista Torricelli, allievo di Galileo, che giunse allo stesso risultato quasi contemporaneamente.
Vediamola in faccia questa curva che, per l'interesse che aveva suscitato a metà del '600, fu definita “la bella Elena” della geometria:

Se la cicloide fu trascurata nella antichità, altrettanto non si può dire della sua cugina, l'epicicloide, ottenuta facendo rotolare un cerchio chiamato epiciclo.
L'epiciclo ha il centro che si muove sulla circonferenza di un secondo cerchio chiamato deferente.
Insomma, la figura che chiarisce tutto è questa.
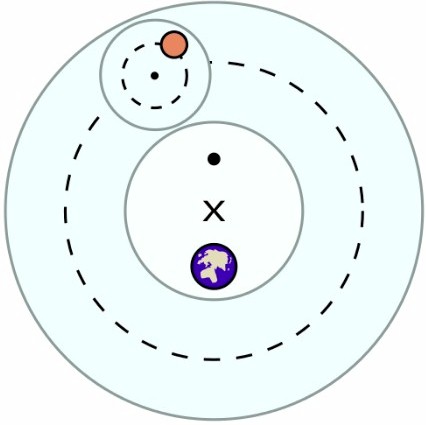
I due cerchi tratteggiati sono l'epiciclo (quello più piccolo) e il deferente (quello più grande, con il centro in X).
L'immagine rappresenta un ipotetico pianeta in orbita attorno alla Terra, secondo la concezione Tolemaica (Terra=centro universo). Vicino al centro, da parti opposte sono rappresentate la terra e l'equante (ma non preoccupatevi, dell'equante non vi diremo nulla in questa sede)
Ideato nel III secolo a.C. da Apollonio di Perga, per descrivere il moto “apparente” dei pianeti sulla volta celeste, questo modello rappresenta le orbite planetarie come un moto composto della rivoluzione del pianeta lungo l'epiciclo e di quest'ultimo lungo il deferente. Largamente utilizzato dagli astronomi greci, diventò uno standard nella cultura antica e medievale per l'influenza dell'almagesto di Tolomeo.
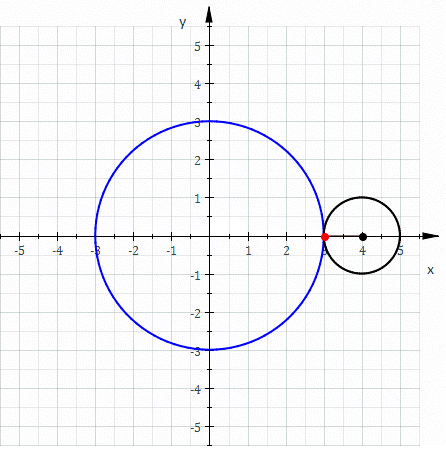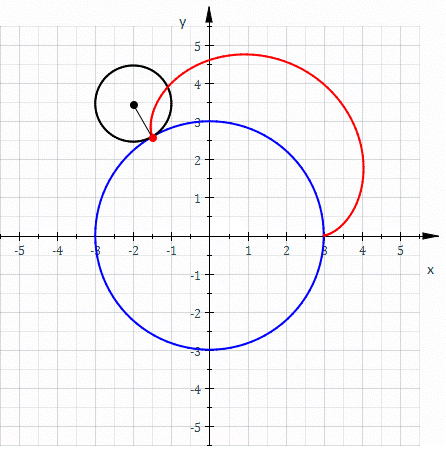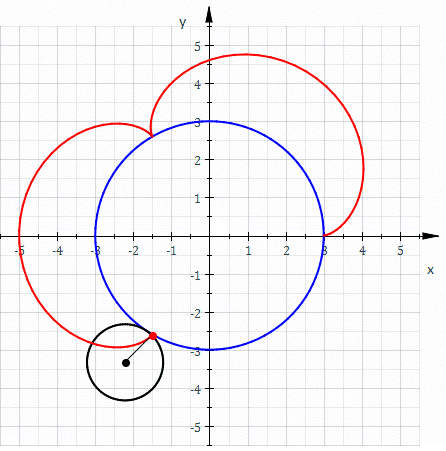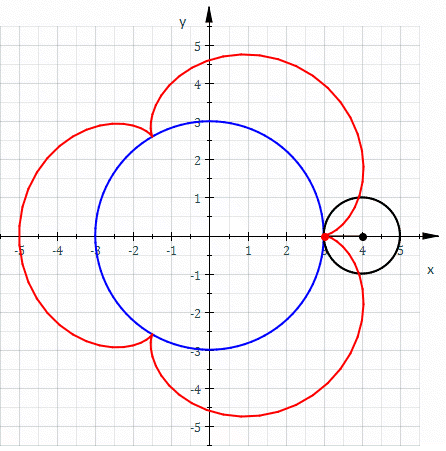
Lo stesso Copernico vi fece ricorso per descrivere il moto della Luna tramite un deferente e due epicicli.
Ma che curva viene descritta da un punto dell'epiciclo? Esattamente una epicicloide ! Cioè una cicloide abbarbicata non al suolo, ma alla circonferenza su cui rotola.
Torniamo ora alla figura del primo quiz sulle due monete...
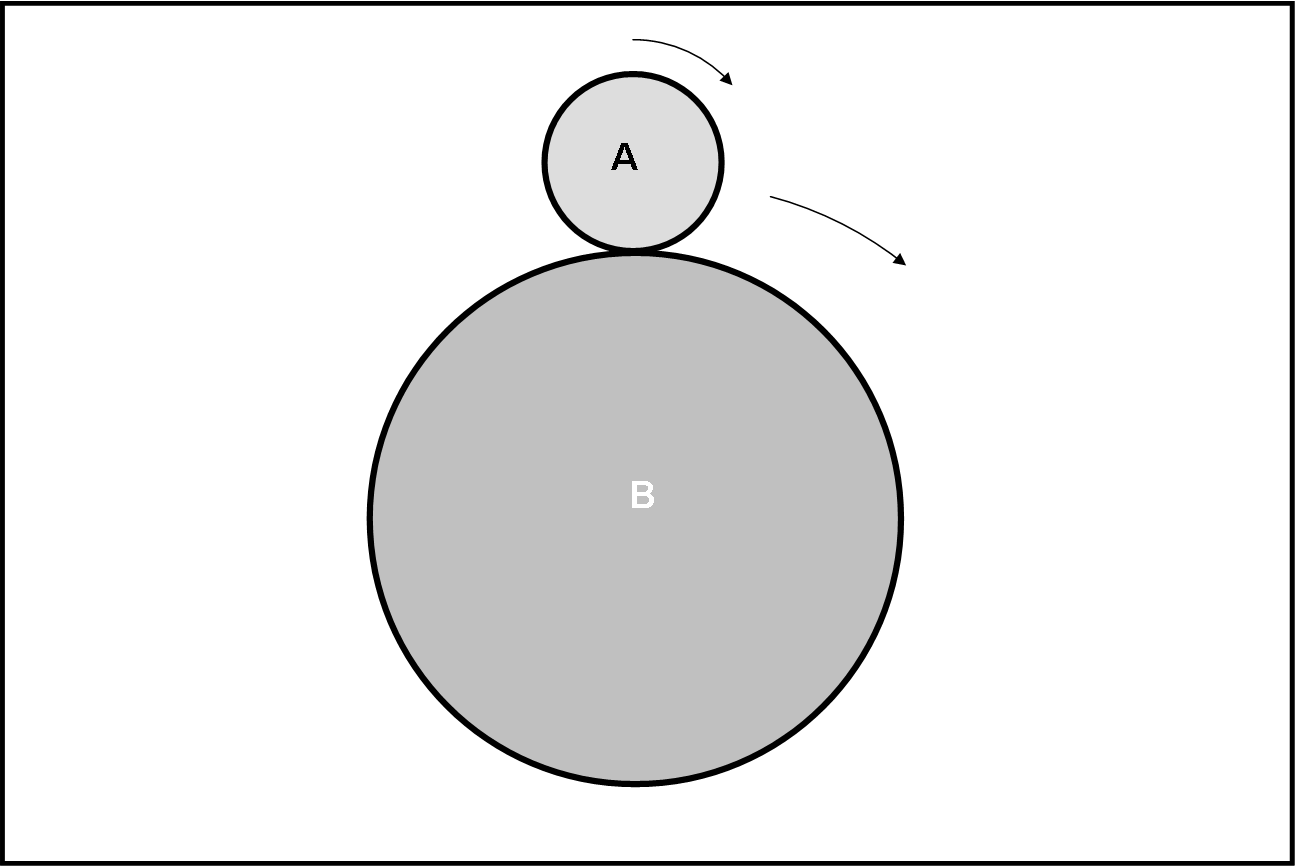
Alla domanda: Quanti giri completi compie la moneta piccola rotolando sulla grande? La risposta di Andy è la seguente:
considero la circonferenza di raggio AB con
AB=(1+1/3)R=(4/3)R C=2π(4/3)R=(8/3)πR
quindi A (centro della monetina) ruotando rispetto a B (centro della monetona) compie un giro completo di lunghezza pari a (8/3)πR ;
il punto di contatto tra monetina e monetona compie un giro completo intorno ad A disegnando una circonferenza di lunghezza pari ad 2(1/3)πR = (2/3)πR e rapportando le due circonferenze:
[(2/3)πR]/[(8/3)πR]= 1/4
che significa che ad 1/4 di giro del punto A intorno al punto B, la monetina ha compiuto un giro completo intorno al suo centro A, quindi per ritornare nella posizione iniziale, la monetina compie 4 giri, con la condizione che la monetina giri intorno al proprio centro A e la monetona sia ferma rispetto al proprio centro B.
E la sua conclusione è ben rappresentata in quest'altra figura...

Dove la faccia del blogger più amato dagli Italiani si fa quattro giri intorno alla monetona.
E per aiutarci a contare i giri si ferma ogni 90°, così riprende anche un po' fiato tra una capriola e l'altra.
Ecco qui... guardatelo, come temerariamente mette a repentaglio la sua incolumità, entrando di persona nella animazione Geogebra (cosa non sarebbe disposto a fare per la Scienza!!!)
Bene, non è finita qui, appena sceso dall' epiciclo, con la testa che ancora gli gira, esprime questo curioso desiderio:
Che ne direste di far vedere l'epicicloide della Luna per distanze diverse Luna-Terra.... che belle figurine!!!!! Mi ricorderebbero Tolomeo....
Per non contrariarlo, ci si da tutti da fare finché si trova in rete un bel video a colori prodotto dal “Planetàri de Milàn” con le immagini evocate. Vale davvero la pena di guardarlo.
Ma intanto si è scatenato anche Pautasso che propone un nuovo quesito.
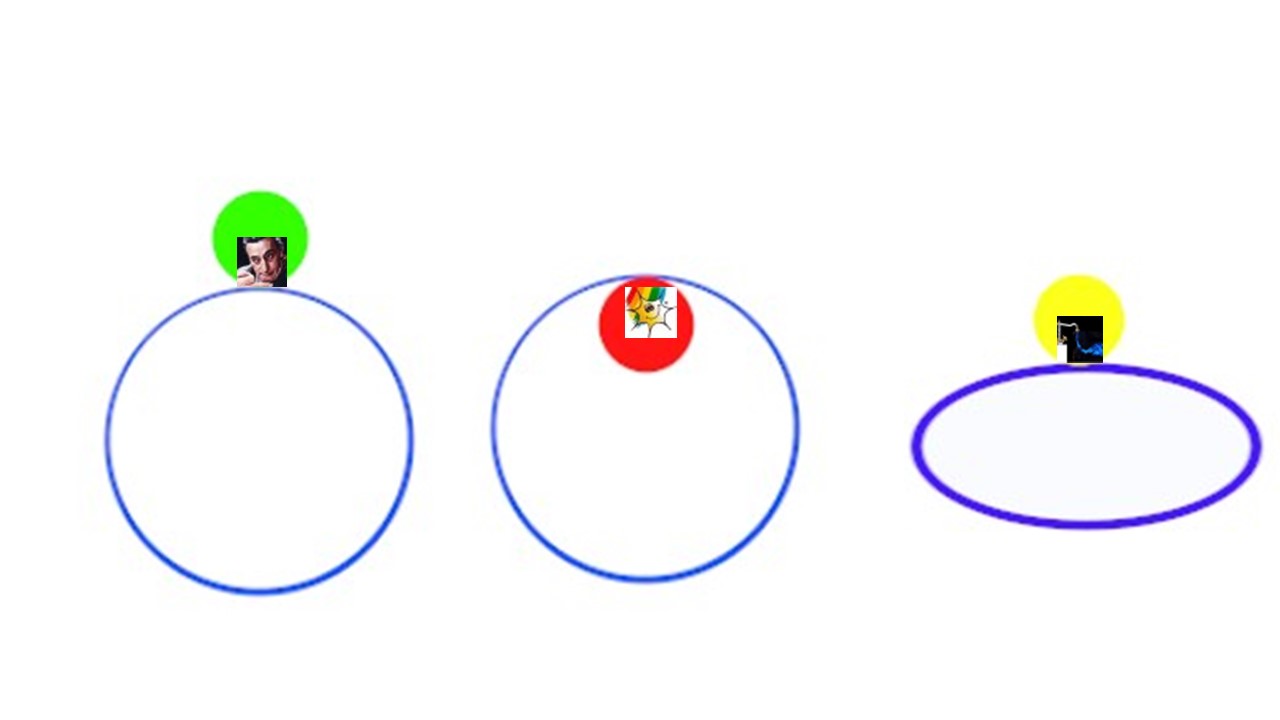
Tre situazioni diverse: monetina con marker “faccia da schiaffi” che rotola esternamente all'anello blu (di diametro triplo), oppure monetina che rotola internamente all'anello blu e, infine, monetina che gira “sopra” l'anello blu sdraiato per terra. Chiede quanti giri completi fa la monetina in ciascuna delle tre ipotesi.
Tanto per capirci meglio, nel secondo caso succede qualcosa del genere...
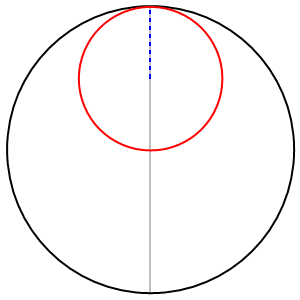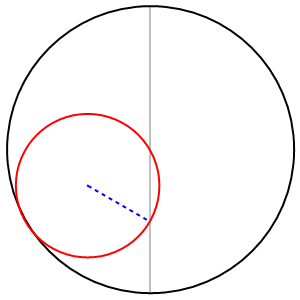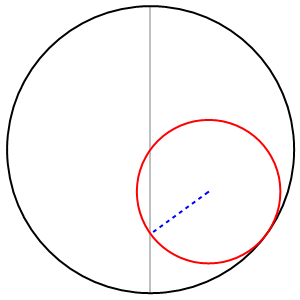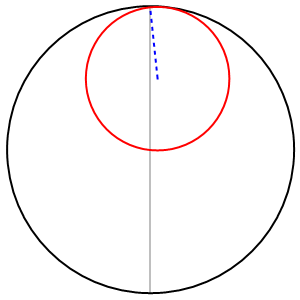
Ma badate bene che, nella animazione, il diametro dell'anello è solo la metà di quello della moneta.
Una figura che rispetta le proporzioni 1:3 potrebbe essere questa. Ve la proponiamo nel formato "faccia generica", così potrete personalizzarla mettendoci la vostra "faccia da schiaffi" preferita.
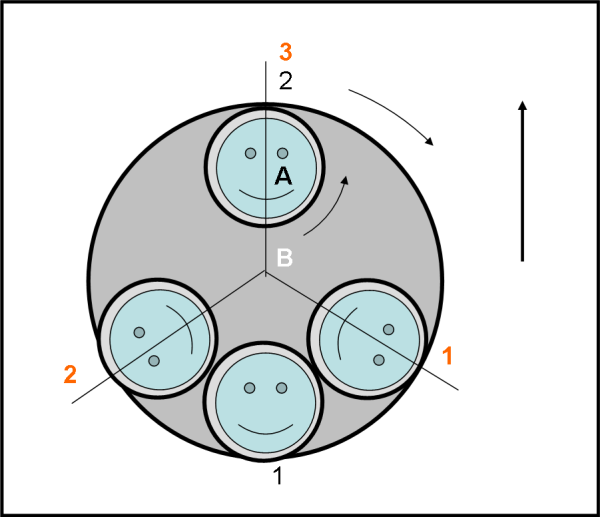
Meno male che Andy vigila e rintuzza subito l'attacco con questa risposta-lampo:
-
Nel primo caso, rientriamo nell’ambito del quiz proposto, dove la distanza AB tra il centro del cerchio fisso B e il centro del cerchio rotante A è pari a 1 + 1/3 = 4/3 e il rapporto: (raggio fisso + raggio rotante) / (raggio rotante) = (4/3) / (1/3) = 4, sta ad indicare il numero di giri compiuti dal cerchio rotante prima di ritornare alla posizione iniziale;
regola generale:
(1 + 1/n) / (1/n) = [(n+1)/n]/(1/n) = n + 1,
con n = {raggio cerchio fisso} / {raggio cerchio rotante},
1 giro del cerchio rotante intorno al suo centro ogni 360° / (n+1) spazzati dalla distanza tra i 2 centri (raggio AB), con centro nel cerchio fisso (B):
360° / 4 = 90°
2) Nel secondo caso (cerchio rosso rotante all’interno del cerchio blu fisso), stesso rapporto raggio fisso / raggio rotante = 3, ma la distanza AB sarà pari a:
R(1 – 1/3) = (2/3)R;
rapporto (raggio fisso - raggio rotante) / (raggio rotante) = (2/3) / (1/3) = 2, che sta ad indicare il numero di giri compiuti dal cerchio rotante prima di ritornare alla posizione iniziale;
regola generale:
(1 - 1/n) / (1/n) = [(n-1)/n]/(1/n) = n – 1,
con n = {raggio cerchio fisso} / {raggio cerchio rotante},
1 giro del cerchio rotante intorno al suo centro ogni 360° / (n-1) spazzati dalla distanza tra i 2 centri (raggio AB), con centro nel cerchio fisso (B):
360° / 2 = 180°.
È interessante notare che in questa ipotesi, nel caso in cui cerchio rotante incluso e cerchio fisso includente abbiano lo stesso raggio, i due cerchi sono contemporaneamente “sovrapposti” e coincidenti, contemporaneamente uno fisso e se stesso in rotazione e l’ipotetica e irrazionale rotazione dell’uno con sé stesso avverrebbe ogni 360° / 0 = infinito spazzati dal raggio AB: la matematica ci dice col suo affascinante linguaggio che c’è qualcosa che non va.

3) Nell’ultimo caso, infine, si ha una sorta di movimento “cicloideo” di un cerchio che, anziché viaggiare su un binario retto, viaggia su un binario curvo a curvatura costante per tutti i suoi punti, e il numero di rotazioni del cerchio rotante per ritornare alla posizione iniziale è pari a:
2πR / [2πR(1/3)] = 3;
regola generale: 1 / (1/n) = n,
1 giro del cerchio rotante intorno al suo centro ogni 360° / n spazzati questa volta dalla proiezione della distanza AB sul piano dove giace la circonferenza di raggio R e centro in B:
360° / 3 = 120°.
Nulla cambia se il piano del cerchio rotante è diversamente incidente rispetto al piano del cerchio fisso: il cerchio di raggio (1/3)R e lunghezza 2πR(1/3) compirà sempre lo stesso percorso di lunghezza 2πR e come poc'anzi, la proiezione della distanza AB sul piano dove giace la circonferenza di raggio R e centro in B, spazza lo stesso angolo, come prima, per ogni rotazione del cerchio rotante intorno al proprio centro.
Ebbene, per non farci mancare nulla, diamo una occhiata anche a come si forma la curva interna che, con poca fantasia , è stata chiamata ipocicloide. Sappiate anche che questa particolare ipocicloide, avendo la faccia da triangolo equilatero e ricordando vagamente la lettera greca "delta", viene chiamata dagli amici "deltoide". Vi mostriamo in questa animazione, per soli adulti, l'inseguimento di due cerchi nell'arena di un anello di diametro triplo, che tracciano la medesima curva deltoide.

A questo punto, per fortuna, si è messo a piovere e se ne sono andati tutti a casa.
Tornato a casa, ecco cosa ha scritto Andy sul suo diario...
Inizio con l'analisi del primo quiz proposto da Enzo.
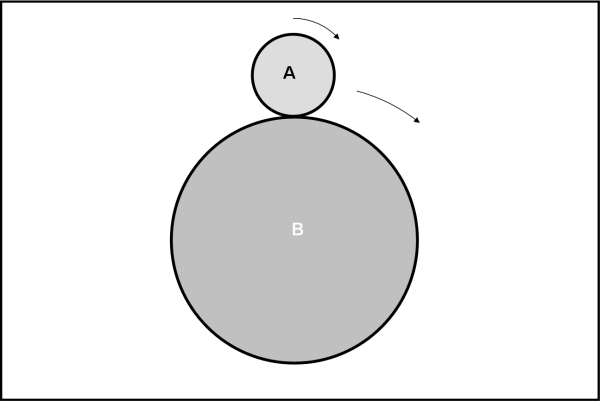
1) Consideriamo la distanza BA tra il centro B del cerchio fisso e il centro A del cerchio rotante, essa è pari al raggio del cerchio fisso BC = R più il raggio del cerchio rotante AC = (1/3)R
ovvero
BA = BC + AC = R + (1/3)R = R + R/3 = (4/3)R.
(raggio del cerchio fisso + raggio del cerchio rotante) / (raggio del cerchio rotante)
Indicando con I il rapporto tra la lunghezza della circonferenza, tracciata da questo raggio BA, con la lunghezza della circonferenza di raggio AC,
si può scrivere:
I = 2π(BA) / 2π(AC) =
= BA / AC = (BC + AC) / AC =
= R(1 + 1/3) / R(1/3) = (4/3) / (1/3) = 4
che determina il numero di giri compiuti dal cerchio rotante attorno al cerchio fisso per ritornare alla posizione iniziale.
In base a ciò, si può ricavare una regola generale per ottenere quanti giri deve effettuare il cerchio rotante affinché possa ricollocarsi nella posizione iniziale:
se n = BC / AC <==> n = {raggio cerchio fisso} / {raggio cerchio rotante}
I = 2πR(1 + 1/n) / 2πR(1/n) = [(n + 1) / n] / (1 / n) = n + 1
Nel caso specifico:
n = BC / AC = R / [(1/3)R] = 1 / (1/3) = 3
I = n + 1 = 3 + 1 = 4
Indicando con θ l’angolo spazzato dal raggio vettore BA in seguito ad una rotazione completa su se stesso del cerchio rotante, è facile verificare che esso sarà pari a:
θ° = 360° / (n+1) = 360° / (3+1) = 360° / 4 = 90°
E ora veniamo alla domanda di Oreste, sulla situazione illustrata in questa figura, dove il cerchio piccolo ruota all'interno della circonferenza grande.

2) In questo caso, il rapporto tra raggio del cerchio fisso e raggio del cerchio rotante è sempre uguale a 3, ma la distanza BA tra i due centri questa volta sarà pari a:
BA = BC – AC = R – R/3 = R(1 – 1/3) = (2/3)R
(raggio del cerchio fisso - raggio del cerchio rotante) / (raggio del cerchio rotante)
Indicando con I il rapporto tra la lunghezza della circonferenza di raggio BA con la lunghezza della circonferenza di raggio AC
si può scrivere:
I = 2π(BA) / 2π(AC) =
= BA / AC = (BC - AC) / AC =
= R(1 - 1/3) / R(1/3) = (2/3) / (1/3) = 2
che determina il numero di giri compiuti dal cerchio rotante attorno al cerchio fisso per ritornare alla posizione iniziale.
In base a ciò, si può ricavare una regola generale per ottenere quanti giri deve effettuare il cerchio rotante affinché possa ricollocarsi nella posizione iniziale:
se n = {raggio cerchio fisso} / {raggio cerchio rotante}
I = 2πR(1 - 1/n) / 2πR(1/n) = [(n - 1) / n] / (1 / n) = n – 1
Nel caso specifico:
n = BC / AC = R / [(1/3)R] = 1 / (1/3) = 3
I = n - 1 = 3 - 1 = 2
Indicando con θ l’angolo spazzato dal raggio vettore BA in seguito ad una rotazione completa su se stesso del cerchio rotante, è facile verificare che esso sarà pari a:
θ° = 360° / (n-1) = 360° / (3-1) = 360° / 2 = 180°
E per concludere, vediamo anche il caso, sempre proposto da Oreste, del cerchio piccolo che si muove sulla traccia del cerchio grande, “sdraiato” sul piano orizzontale.
3) Nell’ultimo caso, infine, si ha una sorta di movimento “cicloideo” del cerchio di raggio AC che, anziché viaggiare su una linea retta, viaggia su una circonferenza di raggio BC.
Indicando con I il rapporto tra la lunghezza della circonferenza di raggio BA con la lunghezza della circonferenza di raggio AC
si può scrivere:
I = 2π(BC) / 2π(AC) = 2πR / [2πR(1/3)] = 3
(raggio del cerchio fisso) / (raggio rotante)
che determina il numero di giri compiuti dal cerchio rotante sul cerchio fisso per ritornare alla posizione iniziale.
In base a ciò, si può ricavare una regola generale per ottenere quanti giri deve effettuare il cerchio rotante affinché possa ricollocarsi nella posizione iniziale:
se n = {raggio cerchio fisso} / {raggio cerchio rotante}
I = 2πR / 2πR(1/n) = 1 / (1 / n) = n
Nel caso specifico:
n = BC / AC = R / [(1/3)R] = 1 / (1/3) = 3
I = n = 3
Indicando con θ l’angolo spazzato questa volta dalla proiezione del raggio vettore BA sul piano dove giace la circonferenza di raggio BC in seguito ad una rotazione completa su se stesso del cerchio rotante, è facile verificare che esso sarà pari a:
θ° = 360° / n = 360° / 3 = 360° / 3 = 120°
Nulla cambia se il piano del cerchio rotante è diversamente incidente rispetto al piano del cerchio fisso: il cerchio di raggio AC compirà sempre lo stesso percorso della circonferenza di raggio BC e come precedentemente, la proiezione della distanza BA sul piano dove giace la circonferenza di raggio R e centro in B, spazza lo stesso angolo, per ogni rotazione del cerchio rotante intorno al proprio centro A.
QUI il testo del primo quiz e QUI il testo del secondo
Se volete sapere qualcosa in più vi conviene dare una occhiata anche QUI e QUI potrete prendere confidenza con un astroide e "costruire" un asteroide!





