Le frecce si abbracciano

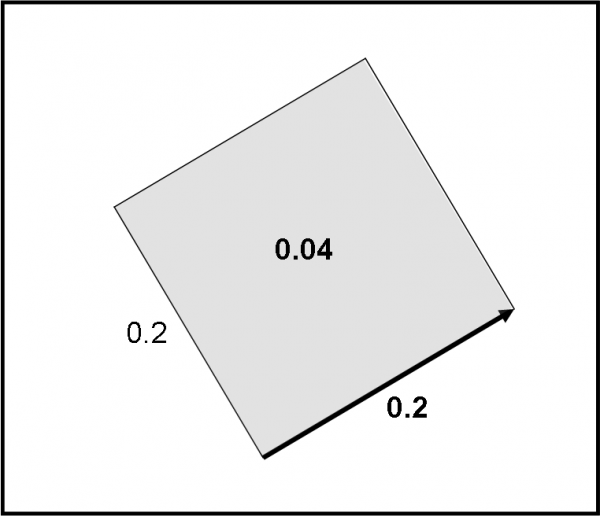
Disegniamo, allora, una freccia e assumiamo che la probabilità che accada un certo evento sia uguale al quadrato della lunghezza della freccia, come mostrato in Fig. 4. Concetto difficile? direi proprio di no e segue una definizione che già avevamo dato nella descrizione del fenomeno della doppia fenditura. Quanto sarà lunga la freccia che indica la probabilità che un fotone si rifletta sulla prima superficie? Sappiamo che la probabilità è del 4%, ossia 0.04. La freccia ha, allora, una lunghezza che è la radice quadrata di 0.04, ossia 0.2. Infatti: 0.2² = 0.04. Matematica veramente elementare, ma che ci regala il mezzo per descrivere come lavora la QED. Sembra impossibile, ma è proprio così.

Dedichiamoci, allora, all’esperimento proposto da Feynman attraverso la lastra di vetro sottile. La conclusione è stata che la probabilità finale dei fotoni riflessi varia da 0 a 16%. Come possiamo rappresentarla in termini di “freccia”? Essa dovrebbe variare in modo tale che il suo quadrato passi da 0 a 16, al variare dello spessore della lastra di vetro. Come già detto la volta scorsa, continuiamo ad assumere che la riflessione avvenga o sulla prima superficie o sulla seconda. Ciò vuol dire che esistono due sole possibilità affinché un fotone raggiunga il rivelatore R1: o attraverso la prima o attraverso la seconda superficie. In qualche modo le due probabilità ad esse relative devono “sommarsi”. La cosa più ovvia è, allora, disegnare due frecce, ognuna relativa a una delle due riflessioni e poi cercare di combinarle in qualche modo in modo che il quadrato della freccia finale sia proprio la probabilità finale dei due eventi. Possiamo già estrapolare questo modo di agire, dicendo che se gli eventi fossero tre, dovremmo combinare tre frecce e via dicendo.

Vediamo, allora, come si possono combinare le frecce (ognuna delle quali si porta dietro la sua probabilità, ossia il suo quadrato) in modo da ottenere il risultato voluto, ossia una freccia che abbia per quadrato la probabilità finale. Non preoccupatevi: il sistema lo conosciamo ormai molto bene attraverso le grandezze vettoriali. Ricordate come si sommano o si sottraggono i vettori? Beh… andate a ripassarlo, ad esempio, QUI o addirittura nella Fisica addormentata nel Bosco. In definitiva vale la famosa regola del parallelogramma. Combiniamo, quindi, le nostre frecce-probabilità proprio come si agisce sommando i vettori. Usiamo la Fig. 5 per spiegarci meglio. Vogliamo “combinare” la freccia x con la freccia y. Spostiamo il vettore y, parallelamente a se stesso, senza cambiargli direzione, verso e modulo, fino a che la sua “coda” coincida con la “punta” di x.  A costo di essere noioso, ricordo ancora che ogni freccia rappresenta la possibilità che un certo evento possa accadere.

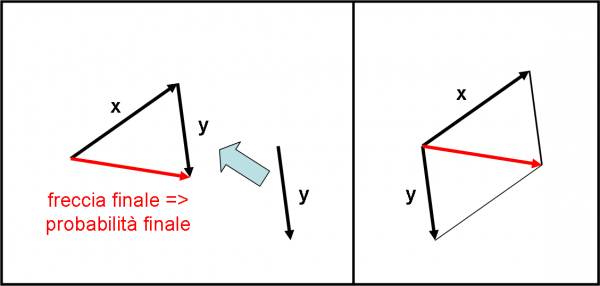
A questo punto non ci rimane che unire la coda della prima freccia con la punta della seconda. La freccia che si ottiene è la combinazione delle due. Avete notato sicuramente  che non abbiamo fatto altro che sommare i vettori x e y. Il vettore finale è la somma vettoriale di x e y.  Feynman fa un bellissimo paragone con la danza. Ogni singola freccia ci indica i passi da fare, volta per volta; la freccia conclusiva indica lo spostamento finale alla fine della danza, ossia il passo che si sarebbe dovuto fare per  raggiungere la posizione finale con un solo spostamento.

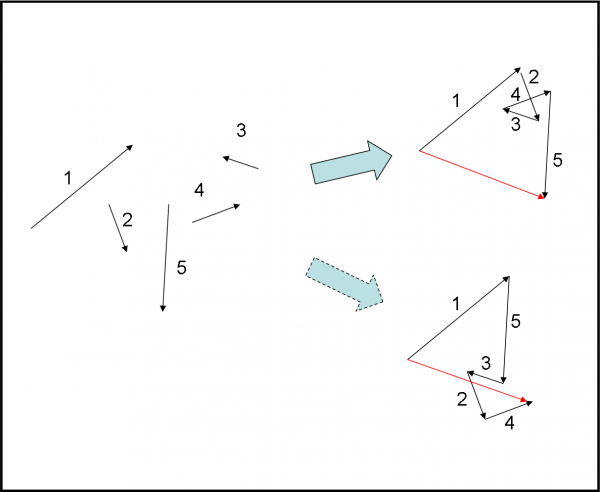
La Fig. 6 ci fa vedere una combinazione in cui abbiamo a che fare con un maggior numero di frecce. Il risultato si ottiene seguendo la regola già descritta. Notate, comunque, che non è importante l’ordine con cui si combinano le frecce: la freccia finale è sempre la stessa.

Procuriamoci un cronometro

Tutto molto bello e soprattutto facile… ma come definire la lunghezza delle singole frecce e -soprattutto- la loro direzione? Per entrare nel caso dell’esperimento della lamina di vetro, le singole frecce sono legate alla probabilità, come già detto, della singola riflessione (nella prima e nella seconda superficie) e la freccia finale alla probabilità della doppia riflessione.  Cominciamo con la lunghezza della freccia. Per la prima superficie, sappiamo già cosa rappresenta: un valore tale che il suo quadrato sia 0.04 (4%), ossia 0.2. La seconda superficie, indipendentemente dal risultato finale che abbiamo osservato, DEVE comportarsi nello stesso modo e quindi anche la freccia relativa deve avere una lunghezza uguale a 0.2.

Il vero problema è quindi definire in modo corretto la direzione di ogni freccia. Solo lei “deciderà” cosa si ottiene dopo la combinazione delle frecce, ossia qual è la somma dei vettori. Ricordiamoci, infatti, del moto circolare uniforme. Due frecce aventi uguale lunghezza (velocità tangenziale) danno luogo a una differenza che non è nulla, ma è uguale all’accelerazione centripeta. Questo semplice esempio ci mostra, ancora una volta, che per poter parlare di MQ bisogna avere una grande dimestichezza con la fisica classica. In altre parole (ripetendomi ancora una volta): per essere Picasso non basta disegnare quadrati e triangoli qualsiasi, ma si deve avere una sapiente conoscenza della pittura dei tempi precedenti.

Feynman ci insegna a calcolare la direzione delle frecce attraverso una geniale descrizione che fa uso di un cronometro speciale, la cui lancetta ruota seguendo il movimento del fotone. Nel caso che sia un fotone “rosso”, il cronometro compie circa 1.440.000 giri per ogni metro percorso dal fotone. Non vi sarà sfuggita una “strana” coincidenza: un giro corrisponde a circa 700 nanometri  (1 nanometro = 10^-9 metri) percorsi dal fotone. Guarda caso questo valore è proprio la lunghezza d’onda della luce rossa… Boccaccia mia stai zitta! Avevo promesso di non interagire con la fisica classica e devo mantenere la promessa.

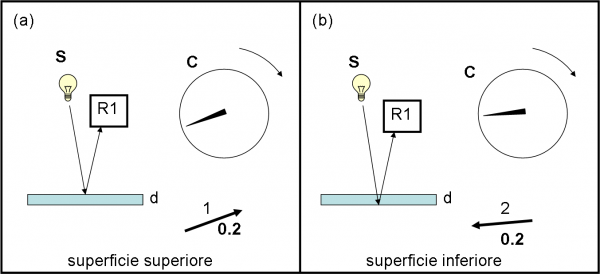
Facciamo partire il cronometro ogni volta che un fotone esce dalla sorgente. Anche se il nostro amico viaggia molto velocemente, il cronometro riesce a stargli dietro e la lancetta gira visibilmente sul quadrante. Schiacciamo con decisione e prontezza il pulsante all’arrivo del fotone in R1 (sempre che sia uno di quelli che arriva su R1, ovviamente). Se il fotone giunge a destinazione riflettendosi sulla prima superficie, dobbiamo considerare come direzione quella della lancetta, ma invertire il verso, come rappresentato in Fig. 7a. Se, invece, il fotone arriva in R1 riflettendosi sulla seconda superficie, la direzione è sempre quella della lancetta, ma il verso rimane quello che è (Fig. 7b). Ovviamente, il fotone attraversa due volte la lastra molto velocemente (la lastra è stata scelta veramente sottile) e quindi arriva su R1, dopo la riflessione sulla seconda superficie, con una direzione della lancetta ben poco diversa da quella che aveva nel caso del fotone precedente. La lunghezza di entrambe le frecce resta quella che è, ossia 0.2, dato che entrambi gli eventi hanno la probabilità del 4% di avvenire.

In Fig. 8 non ci resta che combinare le frecce con il metodo descritto prima e ricavare la freccia finale, il cui quadrato non è altro che la probabilità finale di avere una riflessione, non importa in quale superficie siano avvenute le riflessioni. E’ facile notare che la freccia rossa finale è estremamente corta e quindi la probabilità che capiti l’evento complessivo è veramente vicina a zero (0.0025).

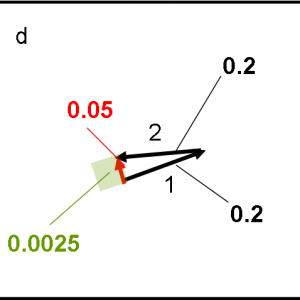
Ridendo e scherzando (e senza aver capito perché) siamo riusciti a calcolare graficamente la probabilità finale di una doppia riflessione. Diventa ovvio dimostrare, in questo modo, che due probabilità possono dare una probabilità finale nettamente più bassa che la “banale” somma delle due. In particolare, più bassa anche di quella della sola prima riflessione (che è del 4%), cosa che continua ad andare al di là della nostra comprensione. Il procedimento, però, funziona, anche aumentando lo spessore d della lastra? Non ci resta che provare.

Le frecce seguono lo spessore e tutto torna

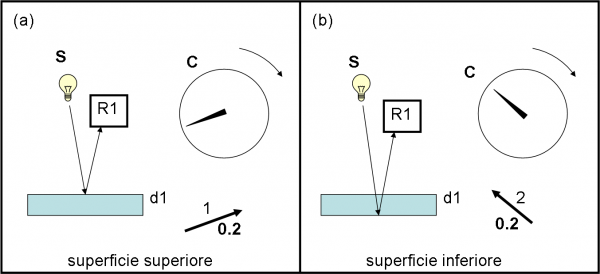
Aumentiamo un po’ lo spessore d portandolo a d1. Il fotone che si riflette nella superficie superiore non cambia assolutamente e la sua freccia resta tale e quale. Il fratellino che si riflette su quella inferiore deve invece percorrere un tragitto più lungo e mentre lo fa il cronometro continua a girare. Quando, finalmente, arriva in R1, la lancetta si è spostata “parecchio” rispetto al caso precedente (Fig. 9a,b).

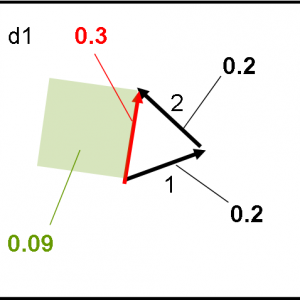
Non ci resta che fare il giochetto che ormai conosciamo bene e che è riportato in Fig. 10. Accidenti! Le cose sembrano proprio funzionare. La freccia finale è diventata più lunga di quelle che l’hanno costruita. La sua lunghezza è, adesso, di 0.3, il che comporta una probabilità finale di 0.09, ossia del 9%. L’aumento dello spessore ha dato molta più possibilità all’evento “riflessione”. Sembra che lo spessore abbia convinto i fotoni a scegliere la strada del “rimbalzo”.

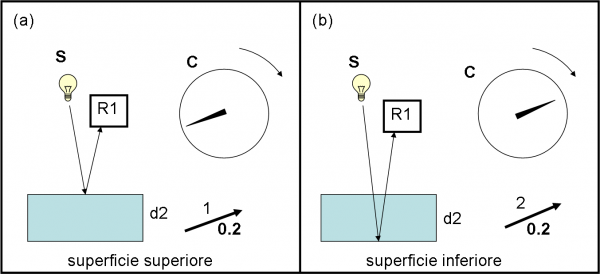
Le cose, però, si fanno ancora più interessanti se aumentiamo ancora lo spessore fino a un certo livello “critico”. Ridisegniamo nuovamente le figure anche se non ce ne sarebbe bisogno. Ma, avevamo promesso di essere elementari e continuiamo in questa direzione. La Fig. 11a,b mostra la situazione del cronometro, della sua lancetta e della freccia relativa. Senza sorprenderci più di tanto (ci siamo abituati alla descrizione senza volere per forza capire), notiamo che la lancetta ha percorso esattamente mezzo giro in più. D’altra parte è logico.

Il tragitto del fotone che rimbalza sulla seconda superficie è aumentato. E’ un gioco da ragazzi disegnare la Fig 12 dove eseguiamo la composizione delle due probabilità. Ci accorgiamo che le due frecce relative vanno nella stessa direzione e che, di conseguenza, la freccia finale ha una lunghezza esattamente uguale al doppio di quella singola. In altre parole, sommiamo proprio i moduli dei due vettori, dato che la direzione è la stessa. Beh… quante volte abbiamo ottenuto lo stesso risultato sommando velocità o altre grandezze vettoriali? In conclusione abbiamo una freccia finale rossa che ha una lunghezza di 0.4. Il suo quadrato è 0.16, ossia la probabilità che un fotone rimbalzi verso R1 è salita al suo massimo, il 16%. Il metodo funziona perfettamente.

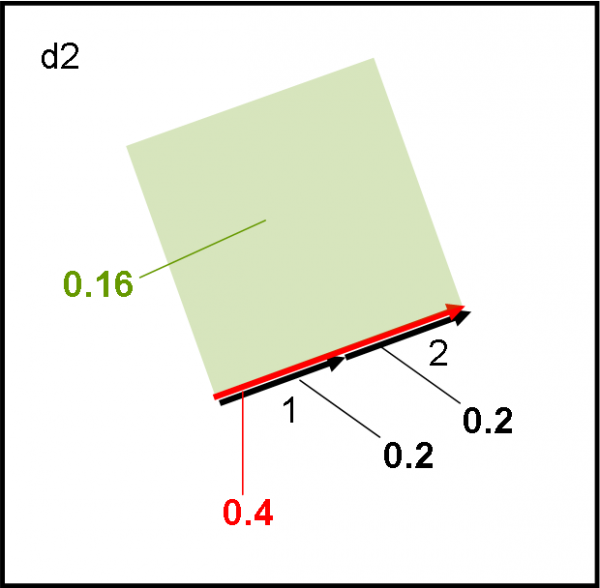
Ricapitoliamo: non sappiamo perché (e preferiamo perfino soprassedere su alcune assurdità sconvolgenti, come quella che sembra dirci che i fotoni che effettuano la prima riflessione decidano di farlo a seconda di come si comporteranno DOPO che i loro amici arrivano sulla seconda superficie) tuttavia, abbiamo escogitato (ops… Feynman ha escogitato…) un metodo di una semplicità disarmante che ci permette di calcolare, comunque, la probabilità finale che un fotone ha di arrivare su R1. Noi l’abbiamo seguito graficamente e senza introdurre la “matematica”, ma esistono formule estremamente complesse che potrebbero definirlo in modo ineccepibile. Ricordiamoci che la QED si basa su una perfetta matematica, ma ha la gentilezza di farsi comprendere anche attraverso operazioni alla portata di tutti.

Potremmo andare avanti aumentando lo spessore, ma il risultato è ormai banale. Se lo spessore raggiunge una certa dimensione la lancetta del cronometro, relativa al fotone che subisce la riflessione inferiore, arriva, nuovamente, ad avere la stessa identica direzione del fotone che è rimbalzato subito. Eseguendo l’inversione della prima freccia, troveremo un risultato ormai ovvio ma pur sempre imbarazzante: la probabilità finale torna a essere zero e avanti così con una periodicità perfetta, così come è perfetta la rotazione della lancetta del cronometro. La Fig. 3 dell’articolo precedente è confermata in pieno!

Alcune considerazioni aggiuntive. Abbiamo visto che le direzioni assunte dalla lancetta nei due casi di riflessione (sulla prima e sulla seconda superficie) anticipano il risultato. Se hanno la stessa direzione e verso, otteniamo una probabilità nulla. Se hanno la stessa direzione, ma verso opposto, otteniamo una massima probabilità (16%). Se le direzioni delle lancette formano un angolo di 90°, l’applicazione del teorema di Pitagora ci dice che la freccia finale è l’ipotenusa di un triangolo isoscele. Ne deriva, subito, che la probabilità finale (quadrato dell’ipotenusa) è il doppio della probabilità di un cateto, ossia di una singola riflessione. Ne segue che  la probabilità finale è data da 2･(0.2)² = 2･0.04 = 0.08, proprio il valore che sarebbe sembrato, a prima vista, il più logico! Lascio a voi la figura che sintetizza questa situazione peculiare che, come già detto, capita due volte a ogni giro della lancetta del cronometro.

Inoltre, teniamo ben presente che la prima freccia rimane sempre la stessa ed è solo la seconda che, pur mantenendo costante la lunghezza, esegue una (o più) rotazioni complete all’aumentare dello spessore.

Fermiamoci un attimo e riassumiamo le idee, dando magari qualche definizione “tecnica”. La lunghezza della freccia viene indicata come ampiezza della probabilità. Una definizione che già conosciamo bene avendone parlato nel caso della doppia fenditura (ricordate). In particolare, segue immediatamente che la probabilità di un evento è uguale al quadrato dell’ampiezza di probabilità. Penso che non sfugga a nessuno l’analogia con un’onda, un’onda di probabilità… come d’altra parte già ci aveva mostrato la Fig. 3. Faccio questa piccola concessione alla fisica, più o meno classica, proprio perché fa già parte della MQ.

Bisogna poi che si sia veramente onesti, così come lo è stato Feynman. In realtà non abbiamo veramente imparato a calcolare la probabilità di un evento (o meglio ancora, l’ampiezza di probabilità di un evento), ma, più giustamente, abbiamo “provato” (con successo) a trovare l’ampiezza di probabilità il cui quadrato sia proprio la probabilità che un evento ha di verificarsi. Tra le due frasi vi è una profonda differenza concettuale.

Coloriamo le frecce

A questo punto, merita tornare sul famoso codice o numero o frequenza che caratterizza un fotone. Esso determina anche il suo colore. Facciamo, allora, un altro semplice esperimento: stendiamo uno strato sottile di olio sul pavimento, magari proprio quello molto sporco -e praticamente nero- della nostra automobile. Illuminiamolo con fotoni che hanno tutti lo stesso codice, ad esempio quello  rosso. Cosa vediamo? Delle zone rosse che si mischiano a zone quasi completamente nere. Come si spiega questo fenomeno, sulla base di quanto abbiamo appena descritto? Non è certo difficile trovare una descrizione logica a seguito di una spiegazione incomprensibile. Lo strato d’olio si comporta come uno strato di vetro ed è sicuramente lontano dall’avere lo stesso spessore in ogni sua parte. Cosa succede allora? Nelle zone in cui è più sottile (o più spesso), la doppia riflessione può portare al valore zero della probabilità di riflessione e, quindi, nessun fotone torna indietro: l’olio rimane scuro. Dove, invece, lo spessore è più grande (o più piccolo), la doppia riflessione raggiunge la massima probabilità di accadere e quindi un bel numero di fotoni rossi rimbalza facendo assumere all’olio un colore rosso più o meno acceso. Dato che lo spessore cambia in modo abbastanza continuo, si vedranno bande rosse separate da bande nere relativamente più strette.

Analoga situazione capita se usiamo fotoni blu (codice diverso). Si ottengono, per la stessa identica ragione, bande blu separate da bande nere.

Proviamo, adesso, a inviare sullo strato d’olio sia fotoni rossi che blu. Il risultato è un bellissimo spettacolo di bande blu, rosse , quasi nere e altre di colori intermedi. Come mai? Elementare (o quasi)! Il codice del blu è diverso dal codice del rosso: il primo è decisamente maggiore ossia la sua frequenza è maggiore. Ciò vuol dire che la freccia del fotone blu gira più velocemente di quella del fotone rosso. Ammettendo (e non vediamo proprio perché non si debba farlo) che il comportamento della curva di probabilità sia la stessa per entrambi i fotoni, la luce blu riesce a completare il proprio ciclo probabilistico durante una variazione di spessore minore rispetto a quella necessaria al completamento di un ciclo della luce rossa.

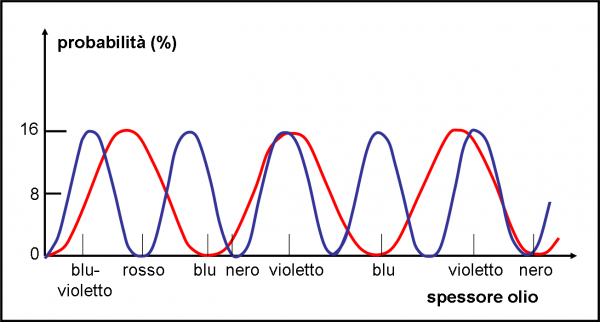
Graficamente (e più facilmente) questa situazione è mostrata in Fig. 13 che altro non è che la Fig. 3 in cui sono stati sovrapposti i due tipi di fotone. Per un certo spessore, ad esempio, la probabilità dei fotoni blu di giungere in R1 ha già raggiunto il valore massimo, mentre quella dei rossi è ancora a “mezza strada”. Vi sono molti tipi di combinazione… Può capitare che il blu sia al massimo e il rosso al minimo (vediamo solo luce blu), oppure sia il blu che il rosso arrivano al massimo (mix perfetto dei due colori), oppure è il rosso che raggiunge il massimo mentre il blu è al minimo. Capita, ovviamente, anche che entrambi i colori siano al minimo del ciclo (colore nero, nessuna riflessione).

Se poi l’olio è versato sopra uno strato di acqua in movimento, ci dobbiamo aspettare che esso continui a variare localmente il suo spessore, comportando una continua variazione delle bande colorate. Figuriamoci, poi, cosa può succedere se quella che arriva è la luce solare, che contiene tutte le frequenze dell’ottico. Una meraviglia iridescente. Beh… l’aggettivo è scelto bene, dato che il fenomeno si chiama proprio iridescenza.

Avete capito benissimo che questo tipo di risultato potremmo spiegarlo benissimo considerando concetti come lunghezza d'onda, indice di rifrazione, dispersione della luce, cammino ottico, interferenza, e molte altre cose che sono di dominio (quasi) pubblico. Tuttavia, lo scopo della QED è proprio quello di descrivere tutto ciò che la fisica ha già dimostrato, basandosi sul calcolo delle probabilità. Solo così si possono “risolvere” problemi ben più generali e del tutto inaccessibili alla fisica classica.

A questo punto, abbiamo in mano lo strumento per il calcolo della probabilità finale di una certo evento. Per convincerci ancora di più della sua validità, applicheremo le nostre frecce e la loro combinazione ad altri fenomeni, come l’andamento rettilineo della luce, l’uguaglianza degli angoli di incidenza e riflessione, la capacità di concentrare la luce da parte di una lente, e tutto ciò che conosciamo attorno alla luce.

Alla prossima e viva Feynman!