Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Sfruttando i salti di un canguro papalliano (i canguri di Papalla sono perfettamente rotondi, ovviamente, e rimbalzano facilmente) affrontiamo il problema dell'urto anelastico, dopo che l'effetto Compton ci ha permesso di studiare gli urti elastici. Un vecchio quiz, ci permette un nuovo approfondimento di meccanica.

Descriviamo un altro tipico gioco papalliano che in qualche modo può assomigliare a quello dell’elettrone che va avanti e indietro tra due papalli che viaggiano uno verso l’altro (QUI). In questo caso, però, l’esercizio viene svolto da un singolo papallo in una zona particolare del loro pianeta, l’unica in cui esiste l’attrito e che, soprattutto, non permette di rimbalzare in modo perfetto sul terreno.

In poche parole, un papallo che si lanci da un trampolino verso il basso rimbalzerà sicuramente sul terreno, ma non riuscirà a tornare alla stessa altezza di prima e la cosa si ripete quando tocca nuovamente il terreno. Insomma, i rimbalzi sono sempre meno alti e prima o poi è costretto a fermarsi. In modo “professionale” possiamo dire che l’urto del papallo sul terreno è anelastico, ossia una certa parte di energia cinetica viene trasformata in un altro tipo di energia (calore, ad esempio, ma a noi poco importa), per cui nella risalita non può raggiungere la stessa altezza della partenza… e via dicendo: ogni rimbalzo è sempre meno alto di quello precedente…

Introduzione

Definiamo il coefficiente di restituzione e tramite la seguente formula:

E_CD = E_CP e²         …. (1)

A parole, possiamo dire che l’energia cinetica E_CD dopo l’urto è uguale a quella prima dell’urto E_CP moltiplicata per il quadrato del coefficiente di restituzione.

Il coefficiente può variare, ovviamente, tra 0 e 1. Se e = 0, l’urto è completamente anelastico (non vi è nemmeno un rimbalzo), mentre, se e = 1, l’urto diventa completamente elastico e i rimbalzi proseguono sempre allo stesso modo: l’energia cinetica dopo l’urto è uguale all’energia cinetica prima dell’urto e il papallo continuea ad andare su e giù senza mai fermarsi.

Nella prima parte  vogliamo dimostrare che se vale la (1), allora deve valere anche:

 v_D = - e v_P

dove v_D è la velocità del papallo dopo l’urto, mentre v_P è quella prima dell’urto.

Dimostrato  questo risultato, inizieremo con il vero gioco papalliano. Il papallo si lancia da una certa altezza h con velocità iniziale uguale a zero e cade sotto l’effetto della sola accelerazione di gravità che su Papalla è uguale a quella terrestre (g). Come detto, il rimbalzo lo porta a un'altezza minore e via dicendo fino a che si ferma completamente.

Quanto tempo impiega il papallo per fermarsi al suolo?

Per una trattazione accurata degli urti elastici potete andare QUI (effetto Compton), ma ritroveremo le stesse formule partendo dagli urti anelastici in genere.

Ciò che caratterizza i vari tipi di urto è la legge di conservazione dell’energia cinetica. Essa  rimane valida solo nel caso di un urto completamente elastico. Non vi è conservazione in tutti gli altri casi di urto, in quanto una certa quantità di energia cinetica viene trasformata nell’urto in altre forme di energia (rumore, calore, deformazione, …). La dinamica relativistica ci ha mostrato come si comporti l’energia totale e come si conservi sempre.

Il valore massimo di energia assorbita si ha quando l’urto è completamente anelastico. In questo caso si ha anche come risultato l’unione delle due particelle in gioco che possono proseguire insieme con una certa velocità. Se le due particelle si separano dopo l’urto (muovendosi ognuna con una certa velocità) abbiamo i vari casi di urto anelastico.

Dato che la differenza tra i vari tipi di urto si ottiene attraverso l’energia cinetica, è facile capire perché si è considerato il coefficiente di restituzione e, tale che:

E_CD = e²E_CP

Dove e può variare tra 0 e 1. Nel caso valga 0, siamo nel caso dell’urto completamente anelastico, mentre, se vale 1, siamo nel campo degli urti elastici.

In TUTTI i casi, comunque, deve valere la conservazione della quantità di moto. Ossia quella prima dell’urto deve essere uguale a quella dopo l’urto.

Un commento importante prima di iniziare. Niente ci vieta di considerare una delle due particelle ferma prima dell’urto. Tuttavia, non è assolutamente possibile considerare la particella IMMOBILE, dopo l’urto. Facendo questo, introdurremmo una forza esterna (un vincolo) che obbligherebbe la particella a non subire spostamenti. Ne seguirebbe che la conservazione della quantità di moto non sarebbe più verificata!

Normalmente, per descrivere un urto si utilizza un sistema di riferimento inerziale qualsiasi. Ciò, però, comporta una conservazione della quantità di moto del tipo:

m₁v_1P + m₂v_2P = m₁v_1D + m₂v_2D

dove i pedici P e D si riferiscono a prima e dopo l’urto.

La faccenda non dà grossi problemi, trattando urti completamente elastici, ma può complicare le cose quando si descrivono urti anelastici in genere, dove compare il coefficiente e.

Conviene, allora, cambiare sistema di riferimento e trattare l’urto anelastico generico in un sistema di riferimento solidale con il baricentro (o centro di massa) del sistema delle due particelle. Per far ciò dobbiamo riferire le velocità delle due particelle in gioco al loro centro di massa. Ovviamente, il centro di massa si muove con una certa velocità, dato che cambia da istante a istante la configurazione del sistema.

Il grande vantaggio di questa scelta è quella di avere la quantità di moto totale prima e dopo l’urto sempre uguale a ZERO (come dimostreremo tra poco).

Per riferire le velocità al centro di massa, basta eseguire le seguenti operazioni vettoriali:

v’_1P = v_1P - v_B

v’_2P = v_2P - v_B

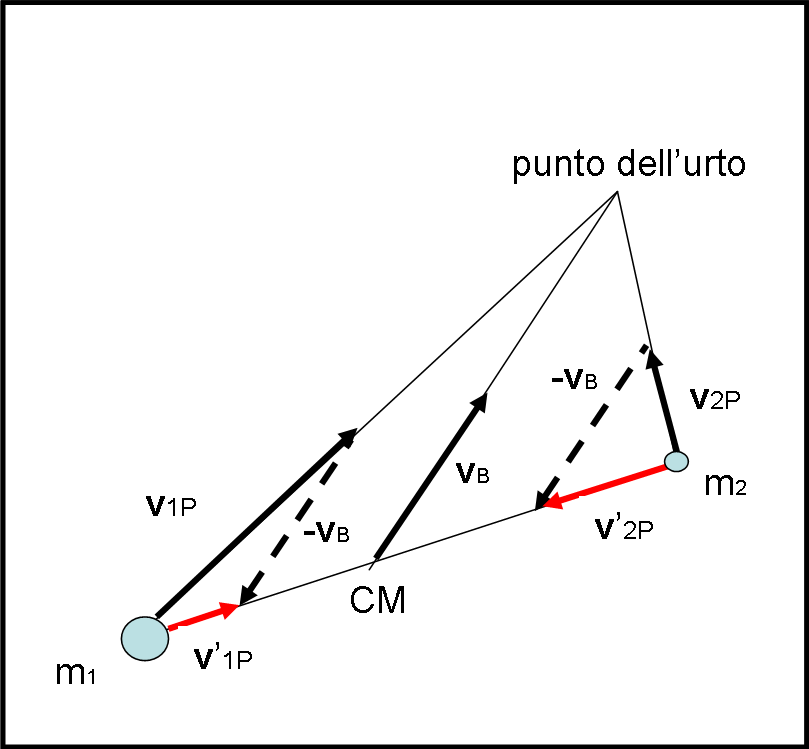
v’_1P e v’_2P sono le velocità delle due particelle prima dell’urto, riferite al sistema del centro di massa, mentre v_1P e v_2P sono quelle del sistema inerziale esterno. La Fig. 1 mostra graficamente la situazione in un urto bidimensionale qualsiasi.

Dimostriamo che la quantità di moto totale prima dell’urto risulta uguale a ZERO.

q’_P= m₁v’_1P + m₂v’_2P = m₁v_1P - m₁v_B + m₂v_2P - m₂v_B = m₁v_1P + m₂v_2P - (m₁ + m₂)v_B

Tuttavia, la velocità del centro di massa può scriversi (ricordando la definizione di centro di massa e derivando):

v_B = (m₁v_1P + m₂v_2P)/(m₁ + m₂)

Sostituendo nella relazione precedente si ottiene:

q’_P = m₁v_1P + m₂v_2P - (m₁ + m₂)v_B = m₁v_1P + m₂v_2P - (m₁ + m₂)(m₁v_1P + m₂v_2P)/(m₁ + m₂)

Semplificando (m₁ + m₂), si ha:

q’_P = m₁v’_1P + m₂v’_2P = m₁v_1P + m₂v_2P - m₁v_1P - m₂v_2P = 0

Analogamente, deve anche essere

q’_D = m₁v’_1D + m₂v’_2D = 0

O, anche:

m₁v’_1P = - m₂v’_2P        …. (1)

m₁v’_1D = - m₂v’_2D       …. (2)

In poche parole, un osservatore piazzato sul centro di massa vede le due masse muoversi verso di lui con quantità di moto uguali e contrarie. La stessa cosa capita dopo l’urto, ma con versi opposti.

Utilizzando queste nuove coordinate si possono ricavare abbastanza facilmente le velocità dopo un urto anelastico. Vedremo che, con e = 1, si ricade nel caso dell’urto elastico che, in un sistema inerziale esterno, avevamo già trattato QUI (effetto Compton) e, con e = 0, nel caso di un urto perfettamente anelastico (vedi dinamica relativistica).

Infine, studieremo il caso in cui la massa di una particella tende a essere infinita e la sua velocità iniziale può essere considerata ZERO.

Urto anelastico

In questo caso non si conserva l’energia cinetica. Le relazioni da considerare sono:

m₁v’_1P = - m₂v’_2P      …. (3)       quantità di moto prima dell’urto

m₁v’_1D = - m₂v’_2D     …. (4)       quantità di moto dopo l’urto

e²(½ m₁v’²_1P + ½ m₂v’²_2P) = ½ m₁v’²_1D + ½ m₂v’²_D2     …. (5)    energia cinetica

Possiamo tranquillamente riferirci a un caso unidimensionale e usare solo i moduli dei vettori.

Le incognite sono, ovviamente, le velocità delle due masse dopo l’urto, v_1D’ e v_2D’.

Dalla (5) si ricava:

m₁(e²v’²_1P - v’²_1D) = m₂(v’²_2D - e²v’²_P2)

ricordando i prodotti notevoli (QUI) si ha:

(a² – b²) = (a – b)(a + b)

E quindi:

m₁(ev’_1P - v’_1D)(ev’_1P + v’_1D) = m₂(v’_2D - ev’_2P)(v’_2D + ev’_2P)    …. (6)

Moltiplichiamo ambo i membri della (3) per e

m₁ev’_1P = - m₂ev’_2P

e le sottraiamo, membro a membro, la (4)

m₁ev’_1P -  m₁v’_1D = - m₂ev’_2P+ m₂v’_2D

m₁(ev’_1P - v’_1D) = m₂(v’_2D -  ev’_2P)      …. (7)

Dividiamo adesso, membro a membro, la (6) e la (7). Possiamo farlo dato che sono due uguaglianze…

ev’_1P + v’_1D = v’_2D + ev’_2P    …. (8)

Le (3) e (4) ci dicono anche che:

m₁v’_1P = - m₂v’_2P

v’_2P = - (m₁/m₂) v’_1P    …. (9)

m₁v’_1D = - m₂v’_2D

v’_2D = - (m₁/m₂) v’_1D   …. (10)

Andiamo a sostituire la (9) e la (10) nella (8)

ev’_1P + v’_1D = - (m₁/m₂) v’_1D - e(m₁/m₂) v’_1P

Siamo riusciti ad avere una relazione con una sola incognita (v’_1D).

Ricaviamola:

v’_1D + (m₁/m₂) v_1D’ = - ev_1P’- e(m₁/m₂) v’_1P

v’_1D (1 + m₁/m₂) = - ev’_1P (1 + m₁/m₂)

v’_1D = - ev’_1P     …. (11)

Siamo ancora nel sistema del centro di massa, mentre noi vogliamo riferirci a Papalla.

Riprendiamo la (8)

 ev’_1P + v’_1D = v’_2D + ev’_2P

e usiamo la (11):

ev’_1P - ev’_1P = v’_2D + ev’_2P

 0 = v’_2D + ev’_2P

E, quindi:

v’_2D = - ev’_2P    …. (12)

Le (11) e (12) risolvono il problema e ci dicono che nel sistema di riferimento del centro di massa le quantità di moto delle due particelle dopo l’urto sono le stesse di quelle prima dell’urto, moltiplicate per e e cambiate di verso:

m₁v’_1D = - m₁ev’_1P      …. (13)

m₂v’_2D = - m₂ev’_2P      …. (14)

le (11) e (12) possono essere riportate al sistema inerziale esterno, ad esempio Papalla, ricordando le relazioni che legano le velocità delle particelle e del centro di massa:

Potete provare a farlo voi e alla fine troverete le due relazioni generali (la soluzione viene data in fondo al capitolo):

v_1D = ((m₁ - em₂)v_1P + (1+ e) m₂v_2P)/(m₁ + m₂)         …. (15)

v_2D = ((1 + e)m₁v_1P + (m₂ - em₁)v_2P)/(m₁ + m₂)         …. (16)

Nel caso in cui e = 1, si ottiene:

v_1D = ((m₁ - m₂)v_1P + 2m₂v_2P)/(m₁ + m₂)

v_2D = ((2m₁v_1P + (m₂ - m₁)v_2P)/(m₁ + m₂)

Proprio le relazioni che avevamo ricavato QUI (formule (5) e (6))

Nel caso in cui e = 0, dobbiamo tener conto che la velocità finale v_D è unica (le due masse si uniscono) ed essa si ricava sia dalla (15) che dalla (16)

v_D = (m₁v_1P + m₂v_2P)/(m₁ + m₂)

In altre parole, la velocità finale è uguale alla velocità del centro di massa prima dell’urto.

Torniamo alla (15) e consideriamo la velocità iniziale della seconda particella (v_2P) uguale a ZERO

v_1D = (m₁ - em₂)v_1P /(m₁ + m₂)

Dividendo numeratore e denominatore per m₂, abbiamo:

v_1D = ((m₁/m₂) - e)v_1P /((m₁/m₂) + 1)         …. (17)

Se la massa m₂ tende a infinito, la (17) si risolve passando al limite:

v_1D = lim _{m2 →∞} ((m₁/m₂) - e)v_1P /((m₁/m₂) + 1) = - ev_1P

Il caso proposto dal nostro quiz può quindi assumere con sufficiente accuratezza che il papallo rimbalzi con una velocità che è praticamente uguale a quella precedente moltiplicata per e (e cambiata di segno).

La faccenda sarebbe leggermente più complicata, dato che la velocità v_2D non può essere ZERO poiché questo fatto comporterebbe la non conservazione della quantità di moto. Essa tende a zero per m₂ che tende a infinito, ma non può essere veramente zero. In realtà, si ha quindi, un leggero allontanamento del riferimento Papalla finale, rispetto al sistema Papalla iniziale. Tuttavia, vale anche la legge di gravità e Papalla viene attirata verso il papallo che ricade, riassumendo la posizione precedente, usata come riferimento fermo, e così via… Insomma, l’approssimazione è più che valida e la possiamo usare tranquillamente.

Soluzione del passaggio da sistema del baricentro a sistema esterno

Abbiamo:

v_1D = v’_1D + v_B

Ma anche:

v’_1D = - ev’_1P

E quindi:

v_1D = - ev’_1P + v_B            …. (18)

Tuttavia, abbiamo anche che:

v_1P = v’_1P + v_B

Ossia:

v’_1P = - (v_B - v_1P)

Sostituendo questo valore nella (18) si ottiene:

v_1D = - ev’_1P + v_B =  - ev_1P + ev_B + v_B = - ev_1P + (1 + e)v_B

Ricordando l’espressione della velocità del centro di massa, si ha:

v_1D = - ev_1P + (1 + e)(m₁v_1P + m₂v_2P)/(m₁ + m₂)

v_1D = (- em₁v_1P - em₂v_1P+ m₁v_1P + em₁v_1P + m₂v_2P + em₂v_2P)/(m₁ + m₂)

v_1D = (- em₂v_1P + m₁v_1P + m₂v_2P + em₂v_2P)/(m₁ + m₂)

v_1D = ((m₁ - em₂)v_1P + (1 + e)m₂v_2P)/(m₁ + m₂)

che è esattamente la (15).

In modo del tutto analogo si ricava la (16).

Prima di dare la soluzione della seconda parte del quiz sul canguro papalliano, vorrei richiamare un semplice problema di cinematica che sta alla base dell’esercizio: la caduta della mela di Newton.

Questa fase di “preparazione” la possiamo dividere in due parti.

La prima non è altro che la caduta di un corpo da una certa altezza; la seconda è il lancio di un corpo verso l’alto e la sua ricaduta.

In entrambi i casi vanno ricordate le leggi orarie del moto uniformemente accelerato. Esse descrivono come variano lo spazio percorso e la velocità del corpo in funzione del tempo che scorre. A loro, tra non molto, si dedicherà anche la fisica papalliana…

s = s₀ + v₀t + ½ at²           …. (1)

v = v₀ + at                        …. (2)

s₀ e v₀ sono la posizione e la velocità del corpo al momento in cui il tempo vale 0, ossia all’inizio del moto; t è il tempo che scorre e a è l’accelerazione che rimane sempre costante. s e v sono la posizione e la velocità per un qualsiasi tempo t. Se proviamo a mettere t = 0, troviamo proprio s = s₀ e v = v₀.

Il Papallo cade

Utilizziamo la Fig. 1

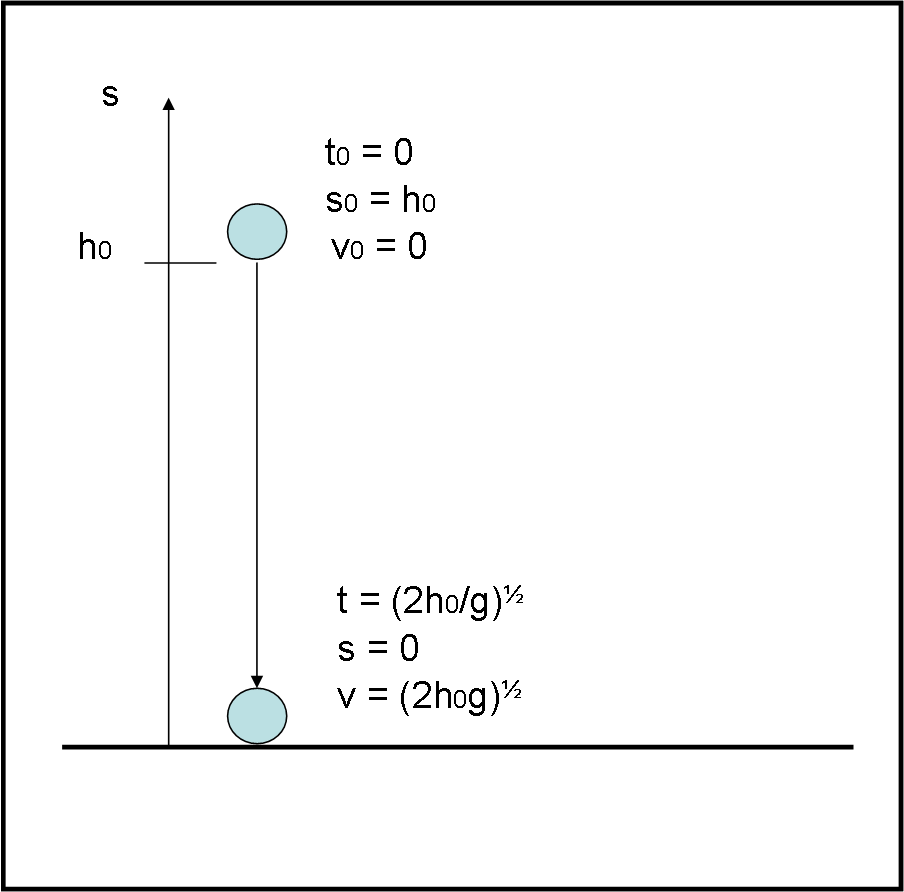
e poniamo il nostro Papallo a un’altezza h₀ dal suolo e lo lasciamo cadere sotto l’azione della gravità. In questo caso abbiamo:

s₀ = h₀

v₀ = 0

a = - g

s = 0

L’origine dell’asse s è il suolo e quindi il verso positivo va verso l’alto. Il Papallo parte da fermo e quindi la velocità iniziale è uguale a zero, così come è zero la posizione finale (il Papallo arriva al suolo). L’accelerazione è quella di gravità che è una costante (g) e che viene presa con il segno meno dato che il verso positivo dell’asse s è verso l’alto.

La (1) diventa:

s = s₀ + v₀t + ½ at² = h₀ + 0 - ½ gt²

ma s è uguale a ZERO, quindi si ottiene la relazione:

0 = h₀ - ½ gt²

E ancora:

½ gt² = h₀              …. (3)

La (2) diventa:

v = v₀ + at = 0 – gt = gt

v = gt                  …. (4)

La (3) ci permette di calcolare il tempo impiegato dal Papallo per arrivare al suolo:

½ gt² = h₀

t² =  (2h₀/g)

t = (2h₀/g)^½         …. (5)

Inserendo la (5) nella (4), otteniamo la velocità con la quale il Papallo arriva al suolo:

 v = gt = g(2h₀/g)^½  =  (2h₀g)^½          …. (6)

Il problema è completamente risolto. Conoscendo h₀ (e, ovviamente, g) si ricavano sia il tempo impiegato a cadere al suolo (5) sia la velocità con cui si arriva al suolo (6).

Se, invece, non conoscessimo l’altezza di partenza h₀, ma solo il tempo impiegato a cadere, basterebbe usare la (3) per ricavare h₀.

Se, infine, conoscessimo solo la velocità di arrivo al suolo, la (6) ci farebbe trovare l’altezza h₀:

v² = 2 h₀g

h₀ = v²/2g           …. (7)

Il Papallo salta e ricade

Manteniamo il solito asse delle s di prima e disegniamo la Fig. 2.

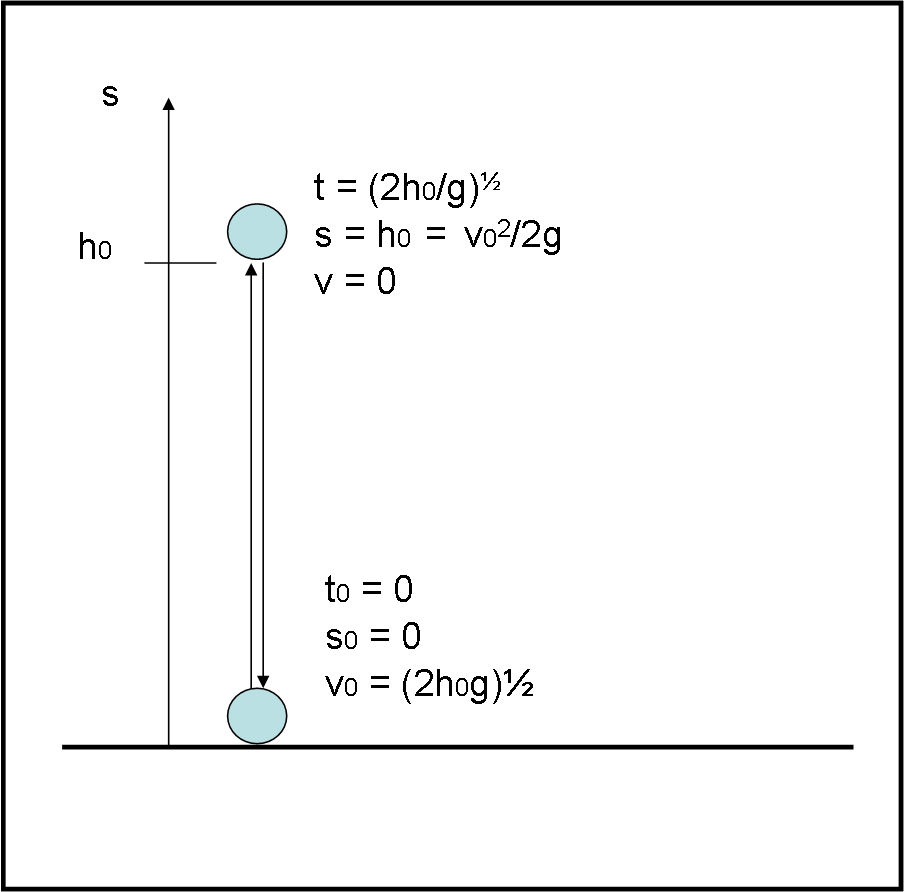
Questa volta il Papallo parte dal suolo con una certa velocità v₀ diretta verso l’alto (positiva). Mentre sale, però, subisce la forza di gravità ed è costretto a rallentare fino a fermarsi per poi ricadere. Analizziamo la salita e vediamo come si trasformano la (1) e la (2).

h₀ = s₀ + v₀t + ½ at² = 0 + v₀t - ½ gt²          …. (8)

h₀ è l’altezza raggiunta, v₀ è la velocità iniziale (costante), - g l’accelerazione di gravità, con il segno meno perché è diretta verso il basso, t il tempo trascorso per giungere nel punto di fermata provvisoria in h₀.

La (2) diventa:

v = v₀ + at = v₀ - gt = 0

da cui:

gt = v₀

t = v₀/g             …. (9)

Dove t è adesso il tempo necessario per raggiungere la massima altezza h₀ con velocità uguale a zero.

Quanto vale l’altezza h₀ (adesso è un’incognita del problema)? Ce lo dice la (8):

h₀ = v₀t - ½ gt²            ….(10)

Il tempo t necessario per arrivare nel punto più alto è dato, però, dalla (9) e basta sostituirlo nella (10), che è poi la (8):

h₀ = v₀ v₀/g - ½ gv₀²/g² = v₀²/g – ½ v₀²/g = v₀²/2g      …. (11)

Attenzione: la (11) è perfettamente uguale alla (7), sostituendo v con v₀. Cosa vuol dire tutto ciò?

Un fatto piuttosto ovvio: l’altezza necessaria per cadere al suolo con velocità v₀ è uguale all’altezza che si può raggiungere saltando con una velocità iniziale v₀.

Quanto tempo impiega il Papallo per arrivare a questa altezza massima? Ce lo dice la (9). Infatti, la (11) afferma che:

v₀²/2g = h₀

v₀ = (2gh₀)^½

Sostituendo questo valore nella (9), si ha:

t = v₀/g = (2h₀/g)^½

che è esattamente la (5).

Insomma, ci siamo divertiti a girare in tondo e a fare un po’ di facili calcoli algebrici. Il succo di tutto è che sia la caduta che la salita portano agli stessi risultati, se la velocità di partenza verso l’alto è uguale alla velocità con cui arriva il Papallo al suolo.

Abbiamo detto una banalità? Assolutamente no, pensandoci un attimo sopra. Questa uguaglianza tra salita e discesa non può che farci concludere che è inutile calcolare tempo e velocità della ricaduta del Papallo. Essi saranno uguali a quelli di salita (e, ovviamente, a quelli di sola caduta della prima parte).

Ne segue che il tempo totale di salita e ricaduta sarà esattamente uguale al doppio del tempo di salita e che la velocità al momento della ricaduta sarà di nuovo v₀.

Uniamo le due parti: un canguro perpetuo

A questo punto possiamo collegare la prima e la seconda parte e avere una specie di moto perpetuo… Il Papallo cade partendo da h₀, tocca il suolo con v₀. Se il suolo lo fa rimbalzare in modo perfettamente elastico la sua velocità diretta verso l’alto è esattamente v₀ (conservazione della quantità di moto) e il Papallo arriva nuovamente fino ad h₀. Poi ricade e tutto continua all’infinito. I tempi di ogni salto (salita e caduta) sono sempre uguali e doppi di quello della prima caduta. Un perfetto canguro instancabile.

Qual è il tempo totale espresso in termini matematici?

Chiamiamo t₀ il tempo di sola caduta iniziale… Abbiamo:

T = t₀ + 2t₀ + 2t₀ + 2t₀ + …… = infinito           …. (12)

E quanto vale la distanza percorsa dal Papallo?

Chiamando h₀ l’altezza della prima caduta, si ha:

H = h₀ + 2h₀ + 2h₀ + 2h₀ + …… = infinito     …. (13)

Un Papallo non perfettamente elastico

Nel nostro problema anelastico, cosa cambia rispetto a questa situazione teorica e perpetua? Solo il fatto che la velocità con cui il Papallo piomba al suolo è maggiore di quella con cui il Papallo risale verso l’alto. La velocità del salto ennesimo è uguale alla velocità del salto precedente moltiplicata per il coefficiente di restituzione e, ossia:

v_n = - ev_n-1

Il segno meno tiene solo conto del fatto che si inverte il moto. Tuttavia, a noi poco importa il segno dato che siamo solo interessati al tempo trascorso e alla distanza percorsa (sempre positivi).

Abbiamo in mano tutti i dati necessari per descrivere lo svolgimento dell’intero esercizio. Basta soltanto usare un semplice ragionamento e la faccenda diventa estremamente banale. In particolare, vedremo che la e entrerà pari pari sia nel tempo che nell’altezza  successiva.

Il primo tempo da sommare è quello di sola caduta (5):

t₀ = (2h₀/g)^½          …. (14)

La velocità con cui arriva al suolo il Papallo, dopo la prima caduta, (chiamiamola u₀) vale (6):

u₀ = (2h₀g)½

la velocità con cui risale il Papallo è (usiamo pure sempre il segno positivo dato che c’interessa arrivare al tempo)

u₁ = eu₀ = e(2h₀g)^½        …. (15)

Il tempo che impiega il Papallo per salire e per scendere è dato da due volte la (9) con la nuova velocità. Ricordando la (14):

2t₁ = 2u₁/g = 2e(2h₀g)^½ = 2et₀      …. (16)

Potremmo già fermarci qui, avendo capito come vanno le cose: il tempo dei prossimo salti completi saranno moltiplicati per e… Proviamolo, usando la (16):

2t₂ = 2u₂/g = 2eu₁/g = 2e²t₀

2t₃ = 2u₃/g = 2eu₂/g = 2e³t₀

…………

Non ci resta che sommare tutti i tempi, sapendo che i salti saranno infiniti. Ma lo sarà anche il tempo totale? Proviamo:

T = t₀ + 2t₁ + 2t₂ + 2t₃ + 2t₄ + ….

T = t₀ + 2et₀ + 2e²t₀ + 2e³t₀ + 2e⁴t₀ ….

T = t₀(1 + 2e(1 + e + e² + e³ + e⁴ + ….))       …. (17)

Fermi tutti! La somma, dentro la parentesi più interna, non è altro che una serie geometrica (QUI). Inoltre la variabile e è compresa tra 0 e 1 e, quindi, la serie è convergente e la somma vale una quantità finita. In particolare:

Σ^∞_n=0 eⁿ = 1/(1 – e)

Sostituendo nella (17), abbiamo:

T = t₀(1 + 2e/(1- e)) = t₀(1 - e + 2e)/(1 - e) = t₀(1 + e)/(1 - e)

Ma sappiamo quanto vale t₀ dalla (14)…

t₀ = (2h₀/g)^½

E, infine, otteniamo:

T = (2h₀/g)^½ (1 + e)/(1 - e)

Dove si vede che se e = 1 (urto completamente elastico) il tempo totale diventa infinito. Negli altri casi il tempo ha un valore limitato, benché i salti siano infinti, ma sempre più bassi…

Se e = 0, il tempo è solo quello della prima caduta, dato che il Papallo si ferma subito non potendo rimbalzare (non vogliamo nemmeno pensare cosa resta di lui…).

Passiamo alla distanza percorsa…

Dalla (7) abbiamo:

h₀ = u₀²/2g        …. (18)

Usando la (11) e sostituendo la nuova velocità.

h₁ = u₁²/2g = e²u₀²/2g = e²h₀

h₂ = u₂²/2g = e²u₁²/2g = e⁴h₀

h3 = u₃²/2g = e²u₂²/2g = e⁶h₀

……………………………………

La distanza totale percorsa dal Papallo è allora data dalla prima discesa h₀ sommata a due volte le altezze di tutti i salti successivi (ogni salto ha una salita e una discesa che devono essere uguali):

H = h₀ + 2h₁ + 2h₂ + 2h₃ + ….

H = h₀ + 2e²h₀ + 2e⁴h₀ + 2e⁶h₀ + …

H = h₀(1 + 2e²(1 + e² + e⁴ + ….))

Abbiamo di nuovo la (17) dove però la serie va con e², ossia possiamo porre:

x = e²

e la parentesi più interna rappresenta una serie geometrica come la precedente:

(1 + x + x2 + x3 +….)

La serie ha quindi come valore:

Σ^∞_n=0 xⁿ = 1/(1 - x)

Ossia:

Σ^∞_n=0 e²ⁿ = 1/(1 - e²)

Da cui:

H = h₀(1 + 2e²/(1 - e²)) = h₀(1 - e² + 2e²)/(1 - e²) = h₀(1 + e²)/(1 - e²)

Con poche formule e molta logica siamo arrivati tranquillamente alla fine (o all’inizio per chi vuole divertirsi con vari valori di e o con altri giochini di estrema semplicità).