Un'ulteriore riflessione prima di andare avanti. Non la inserisco per creare confusione, ma solo perché temo che a qualcuno la trattazione della QED potrebbe sembrare qualcosa che poco ha a che vedere con la MQ “classica” che abbiamo imparato a conoscere attraverso vari fenomeni ed esperimenti apparentemente assurdi. Parole come  “collasso d’onda” e cose analoghe sembrano del tutto trascurate. Ci limitiamo a ripetere, quasi con monotonia, la solita regola che cambia di pochissimo di volta in volta. Sì, tutto bellissimo, ma sembra quasi che i misteri affascinanti e assurdi della MQ non esistano più.

La QED è figlia prediletta della MQ

Per richiamare l’attenzione e ricordare che QED e MQ sono la stessa cosa, facciamo un piccolo ragionamento. Ciò che abbiamo imparato è che la direzione presa da un fotone dopo che è partito dalla sorgente può essere qualsiasi. Non solo, però. Esso ha una sua ampiezza di probabilità intrinseca che è la stessa, qualsiasi direzione prenda. Chiamiamolo pure “particella”, ma sappiamo benissimo che può trovarsi dovunque a un certo istante. A parità di tempo anche la lancetta del cronometro è uguale, qualsiasi sia la direzione presa, per definizione.

Abbiamo, però, imparato che la descrizione di un fenomeno, come la riflessione o la rifrazione, avviene quando un certo numero di traiettorie possibili, non troppo piccolo, mantiene una direzione quasi uguale, ossia riesce a combinare efficacemente le singole frecce (i tempi di arrivo in un certo luogo attraverso una cera traiettoria) e acquista un’ampiezza di probabilità più alta di qualsiasi altro gruppo arrivi sul rivelatore. Questa modalità (traiettoria) diventa la più probabile, ossia quella che “normalmente “avviene. Tuttavia, non dimentichiamoci che le traiettorie percorribili dal fotone arrivano sul rivelatore sempre e comunque con una probabilità uguale a quella di ogni altra sorellina, qualsiasi sia la strada percorsa.

Non confondiamo, quindi, probabilità che si verifichi un certo evento con la probabilità del singolo fotone di partecipare a tale evento in modo costruttivo. Durante il suo viaggio, quindi, qualsiasi direzione del fotone è valida tanto come le altre. Se poi diventa utile per il fenomeno conclusivo è solo una questione di condivisione con altri fratelli di idee simili, sulla scelta del percorso. Tuttavia, il singolo fotone non dirà mai cosa vuole veramente fare fino a che non farà fermare la lancetta del cronometro in un certo luogo. In ogni istante precedente la sua probabilità di essere ovunque è la stessa, piccola, ma reale.

Immaginiamo di seguire come una spia il nostro fotone che sta viaggiando senza comunicare la sua direzione. Non sappiamo dove sia, ovviamente, ma ci affidiamo alla fortuna e al tempo a disposizione: se non va bene con un fotone riproveremo con altro. Finalmente, a un certo momento, gli scattiamo una foto o lo fermiamo con un mano o anche solo lo guardiamo. Cosa abbiamo fatto? Abbiamo stabilito dove si trova esattamente e ovviamente, essendo proprio lì, la sua probabilità di trovarsi in quel luogo diventa il 100%. Non importa come sia disposta la lancetta del cronometro, ciò che conta è che l’ampiezza di probabilità raggiunge il 100%. Immediatamente, tutte le ipotetiche (?) direzioni alternative del fotone cessano di avere validità e scompaiono. Quell’insieme di particelle “virtuali”, ognuna delle quali avrebbe potuto essere quella vera del fotone, spariscono e l’unica particella rimane quella che visto o sentito. L’ho fatta collassare! Vedete come siamo velocemente arrivati a bomba? Visione probabilistica in cui esiste un'ampiezza di probabilità uguale in ogni direzione si trasforma in un qualcosa di veramente concreto che ha l’intera probabilità possibile di esistere lì e solo lì.

Non voglio proseguire in questa direzione perché renderei più complicata una trattazione che deve tener conto di vari principi da un lato e di una semplice regola dall’altro. Affidiamoci a quest’ultima e vedremo che, alla fine, tutto combacerà perfettamente. E salveremo sia le onde (di probabilità) sia le particelle che, da quanto detto, sono la stessa identica cosa. Quando questa perfetta identità ci apparirà chiara e illogicamente logica, potremo dire di aver cominciato a saper descrivere la MQ e a calcolare qualsiasi risultato di qualsiasi fenomeno elettrodinamico e non solo. Scopriremo anche che tanti principi della MQ perdono di valore o -meglio- nascono automaticamente descrivendo la QED.

Se vi dico che Feynman è un  genio assoluto non lo dico tanto per dire! Lo vedremo tra poco quando descriverà con un facilità irrisoria una lente capace di focalizzare la luce di una sorgente in un punto. Sarà un procedimento talmente ovvio da farci pensare che siano le nostre spiegazioni classiche a essere assurde e non il mondo di Alice.

Bando alle ciance e andiamo avanti. Innanzitutto dedichiamoci a scoprire e quantificare meglio le  capacità di un gruppo omogeneo e ben affiatato. Vorremo stabilire dei limiti alla consistenza di un  gruppo affinché sia veramente efficace nel “costruire” e/o definire l’evento di massima probabilità.

Come deve essere un vero “gruppo” quantistico

Per far ciò, non abbiamo bisogno né di specchi né di acqua, ci basta l’aria.  Si abbia la solita sorgente S  e due ricevitori R1 e R2. Vedremo tra poco dove piazzarli. Dato che siamo interessati a studiare il “fascio” di traiettorie che può costruire una probabilità vincente, non ci resta che limitare il gruppo da analizzare. Usiamo uno schermo di cartone o quello che volete (basta che blocchi la luce) con una fenditura al centro, come mostrato in Fig. 31.

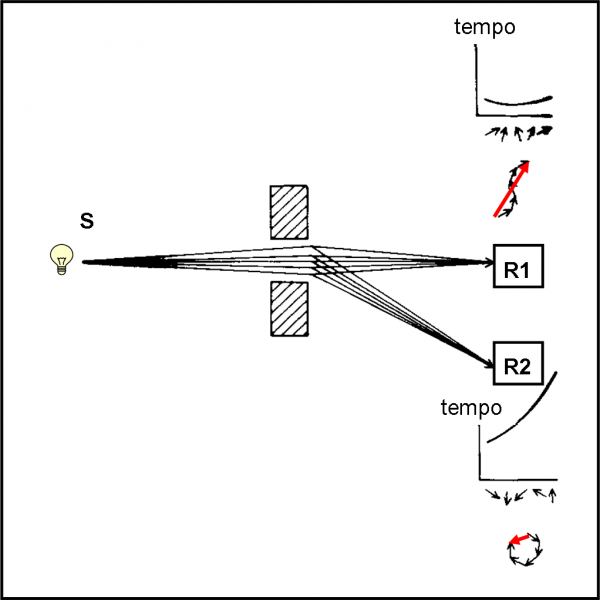
La fenditura non fa altro che limitare le traiettorie  che partendo da S cercano di raggiungere il rivelatore. Poniamo R1 di fronte alla fenditura e R2 in una posizione nettamente più bassa. Ormai sappiamo bene che prima di dire che la luce viaggia da S a R1 con la maggiore probabilità (cosa che l’apparenza del mondo comune sembrerebbe facilmente dimostrare), dobbiamo costruire il grafico che ci indica il percorso effettuato dalle traiettorie che riescono a passare e, con l’aiuto del cronometro, la direzione di ogni singola probabilità. Essendo il tragitto SR1 il più corto e dato che il mezzo da attraversare è sempre lo stesso, sappiamo benissimo che le frecce si sommeranno in modo costruttivo, differendo di pochissimo in quanto a tempi di percorrenza. Prendiamo pure una fenditura abbastanza larga, tanto per cominciare, e poi la stringeremo sempre di più, proprio per capire fino a che punto si può ridurre il gruppo delle traiettorie vincenti.

Per maggiore sicurezza (anche se ci immaginiamo il risultato) leggiamo anche ciò che dice il rivelatore R2. Il discorso è sempre lo stesso: le frecce intorno alla traiettoria rettilinea SR1 si sommano nella parte centrale e danno una grande probabilità al gruppo corrispondente. Quelle, che invece colpiscono R2 (facendo un percorso un po’ strano ma SEMPRE possibile) litigano fra loro, si annodano e danno un risultato praticamente nullo. In poche parole ben poca luce raggiunge R2, come ci saremmo aspettati vivendo la realtà comune.

Tuttavia. Vediamo che anche buona parte delle traiettorie che arrivano in R1 servono a poco. Beh … lo sapevamo già: quelle più al bordo impiegano troppo tempo rispetto a quelle centrali e le loro frecce non costruiscono niente di buono. A questo punto, niente ci vieta di ridurre un po’ di più la larghezza della fenditura, in modo da fare entrare SOLO le traiettorie utili a costruire la probabilità finale. Il  risultato ci conforta: la probabilità della traiettoria QUASI rettilinea non cambia, e quella rivelata da R2 rimane ben poco significativa.

L’appetito vien mangiando (Fig. 32)… e riduciamo ancora di più la fenditura, che diventa molto piccola e taglia fuori anche molte delle traiettorie che sarebbero potenzialmente utili. Se la fenditura è troppo stretta, le cose si complicano di molto e ci riportano con i piedi per terra e rispolverano l’assurdità apparente della MQ. La luce che raggiunge R1 s’indebolisce. Niente di strano, dato che arrivano meno traiettorie. Tuttavia, anche la probabilità finale si riduce. Anche questo è ovvio, dato che abbiamo meno frecce da combinare assieme.

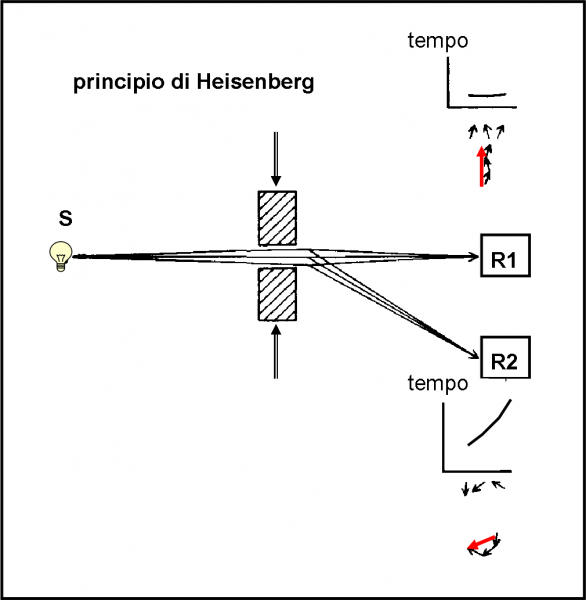
La sorpresa è, invece, che, improvvisamente, anche R2 comincia a rivelare fotoni e la loro probabilità finale diventa comparabile con quella ottenuta in R1. In poche parole, per una fenditura molto stretta la probabilità si sparpaglia su rivelatori posti anche molto distanti tra loro. La spiegazione è ovvia, in termini di QED. Benché i tragitti da S a R2, siano più lunghi di quelli da S a R1, le differenze tra di loro sono sempre meno evidenti e, a causa anche del piccolo numero di frecce da sommare, capita facilmente che la freccia finale abbia la stessa lunghezza.

La combinazione delle frecce relative a R1 e R2 le vediamo nella parte destra della Fig. 32. Ripetiamo ancora. Restringendo la fenditura, diminuisce l’intensità luminosa (ossia il numero di fotoni che arrivano o la probabilità  delle traiettorie ammissibili). Analogamente diminuisce, però, la probabilità finale del percorso considerato ufficiale ( rettilineo e  più corto). Diminuisce a tal punto che anche  altri rivelatori, posti un po’ ovunque, possono ora competere con la probabilità, fino a quel punto dominante. Anzi, la loro probabilità aumenta grazie proprio al piccolo numero di frecce da sommare. In pratica, succede che, per una fenditura molto stretta la luce arriva in punti diversi dello schermo finale (ossia in rivelatori diversi) mantenendo una probabilità di accadere praticamente uguale. Non voglio assolutamente sconfinare nella diffrazione e cose del genere (ma è ovvio che la figura di diffrazione dipende dall’ampiezza della fenditura come ci insegna la QED). Diventerebbe un po’ troppo difficile, anche se alla portata della QED e delle sue leggi. Sappiamo o non sappiamo che riesce a spiegare ogni fenomeno ottico?

C’è bisogno di Heisenberg?

Tuttavia, è giusto e doveroso fare una considerazione della massima importanza. Quando stringiamo la fenditura sempre di più, cosa stiamo facendo? Cerchiamo di determinare sempre meglio qual è la posizione del fotone prima che si diriga verso il rivelatore “prescelto”. Facendo questo, però, ci siamo accorti che diventa sempre più difficile prevedere probabilisticamente quale sarà la direzione scelta. Con la fenditura larga capita, invece, il contrario: non sappiamo molto bene dove passa il fotone all’interno del foro, ma sappiamo molto bene la direzione che prenderà dopo, con grande probabilità, ossia quella del rivelatore R1.

Ma che cosa  abbiamo appena enunciato? Sì, cari amici, nient’altro che il principio di indeterminazione di Heisenberg, uno dei capisaldi della MQ, proprio quello che ci permette di rendere plausibile la nascita dell’Universo e dell’inflazione. Vedete come tutto è strettamente collegato.

Senza i fotoni che scelgono una direzione e sommano le  freccette delle loro probabilità, il principio di Heisenberg rimarrebbe senza descrizione e di conseguenza il nostro Universo potrebbe non nascere o essere nato (che è, infondo, la stessa cosa). Ripeto ancora: il dire che se riesco a determinare con esattezza la posizione non riesco a determinare altrettanto bene la sua direzione ( e viceversa) è un’ovvia conseguenza della QED. Il principio di Heisenberg potrebbe non essere nemmeno enunciato, dato che è un passaggio obbligatorio

Bene, ridendo e scherzando abbiamo imparato cosa s’intende per fascio stretto  e, soprattutto, che non bisogna esagerare a renderlo stretto e preciso, dato che subentra il principio di Heisenberg e tutto si complica. Complicazioni che sono perfettamente previste dalla QED.

La lente? Un piccolo e banale trucco probabilistico!

Affrontiamo, adesso, un’applicazione fantastica di tutto ciò che abbiamo imparato finora. Per la prima volta non saremo calcolatori passivi, ma cercheremo di “agire” in modo da ottenere un risultato altamente utile per le osservazioni “normali”. Useremo ciò che conosciamo delle regole della QED per costruire uno strumento fondamentale atto a osservare gli oggetti dell’Universo. Vi rendete conto dell’enorme portata concettuale di questa asserzione? Se solo Galileo Galilei avesse conosciuto la QED, non si sarebbe sorpreso più di tanto delle sue scoperte astronomiche…

Consideriamo la solita sorgente S e un rivelatore che questa volta chiamiamo F. tra poco vedremo il motivo di questa scelta… I fotoni sono liberi di andare dove vogliono, come al solito, e di raggiungere F con qualsiasi traiettoria. Noi continuiamo a disegnare traiettorie rettilinee per pura semplicità, ben sapendo che lo possiamo fare senza alcun rischio.

Immaginiamo di tracciare una retta verticale “virtuale”  nella Fig. 33, che ci permetta di considerare solo le traiettorie che, arrivate su quella linea, piegano per andare verso F. Una scelta che però non lede minimamente le probabilità intrinseche di ogni singola traiettoria (la freccia è uguale per tutte, disegnate o no). Come rappresentiamo il solito diagramma tempo- posizione? Nel solito, addirittura noioso, metodo. Il tempo decresce andando verso traiettorie rettilinee e le frecce si muovono sempre meno rispetto alla precedente e alla successiva, avvicinandosi alla traiettoria che viene percorsa nel minor tempo possibile.

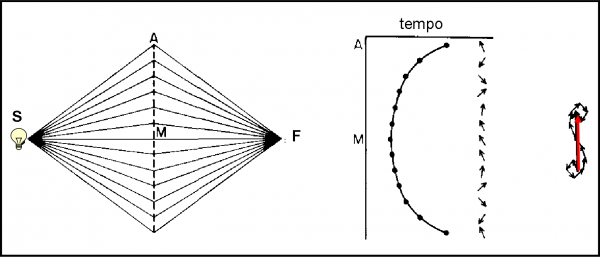
Prendiamo le frecce e componiamole assieme. Ancora una volta il centro della figura è favorito e le traiettorie vicino a quella di minimo percorso e di minor tempo (la rettilinea) hanno la massima probabilità di essere seguite.  Insomma, non abbiamo ottenuto altro che le frecce lontane si annullano e quelle vicine si sommano: una scarsa soddisfazione, senza aver imparato niente di nuovo.

Tuttavia, sappiamo anche che se un fotone attraversa un mezzo diverso, come l’acqua o il vetro, il cronometro gira più lentamente.  Perché allora non intervenire direttamente sulle traiettorie della Fig. 34 e costringerle a impiegare TUTTE lo stesso tempo per arrivare in F? Difficile? Mica tanto, basta inserire per ogni tragitto una parte di vetro da affrontare più lentamente (come il bagnino nell’acqua). Questa percorso in un mezzo diverso deve essere, ovviamente, più lungo per la traiettoria originariamente più veloce e praticamente nullo per quelle ai bordi della retta (A) che già impiegavano un tempo considerevole.

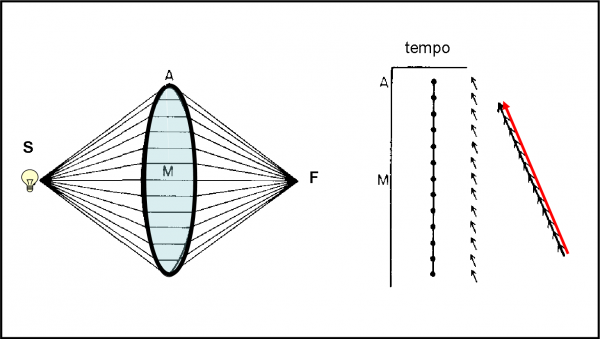
Insomma, inserendo un pezzo di vetro (l’acqua non è facile da maneggiare) possiamo costringere tutte le traiettorie  a essere percorse  nello stesso tempo per raggiungere il punto F. In tale caso come si trasforma la combinazione delle frecce di probabilità? Facilissimo a dirsi e a calcolarsi: tutte le frecce sono lunghe uguali (per definizione) ma sono anche dirette tutte nella stessa direzione, dato che il tempo finale impiegato per passare da S a F è uguale per tutte (il cronometro, alla fine, ha la lancetta che punta sempre nella stessa direzione). Accidenti! Otteniamo una probabilità altissima, a cui concorrono TUTTE le traiettorie che colpiscono la retta “virtuale”. Questa ormai non ha più senso di essere disegnata: da come abbiamo agito, è stata sostituita da un pezzo di vetro di  spessore variabile, massimo nella direzione orizzontale SF e nullo nelle direzioni dei bordi.

Insomma, abbiamo costruito nientedimeno che una lente convergente, capace di produrre in F una probabilità altissima di ricevere tutta la luce che proviene da S e che incontra la lente. E l’abbiamo costruita fidandoci completamente (e giustamente) delle regole incomprensibili (lo sono ancora tanto?) ma descrivibili della QED.

Viene spontanea una conclusione logicissima in termini di MQ: se aumento la lunghezza della lente (il diametro)  la probabilità che tutta la luce raggiunga il fuoco sale notevolmente. Un modo diverso, apparentemente assurdo, per dirci che è meglio, quando si può, usare una lente il più grande possibile. Qualcosa in più del dire solamente: “Più è grande e più raccoglie luce”.

Geniale, decisamente geniale! La QED, senza alcuno strano artificio ci ha permesso di costruire uno strumento capace di concentrare, in un singolo punto, la luce di una sorgente con una probabilità altissima. Tutte le ricadute sul diametro, su lenti multiple, su fenomeni di aberrazione, su lenti divergenti, su ingrandimenti, ecc., ecc. vengono risolte e descritte continuando a ragionare con le stesse identiche regole. Tutta l’ottica dei telescopi può essere descritta in termini probabilistici, con l’uso di una freccia sempre uguale, un  cronometro preciso e una banale somma di vettori. E poi diciamo che la MQ è assurda! Comincia a sembrare più logica di tutte quelle sigle inutili che accompagnano i telescopi e la loro ottica. Oculari, lenti di Barlow, tipo di combinazione ottica, luminosità , campo di vista, ecc., ecc.? Nessun problema! Basta chiedere alla QED di seguire le sue solite regole che ormai conosciamo quasi perfettamente.

Chi vuole provare può farlo. Le difficoltà non sono poi insormontabili. Un esercizio, comunque, più utile che ipotizzare universi senza capo né coda…

Complichiamo un po' il processo di calcolo

Siamo arrivati a un  punto importante, direi a una svolta. Dopo aver imparato così bene a calcolare la probabilità che un certo evento avvenga, ecco che adesso vi chiederò di dimenticare per un po' la combinazione delle frecce di probabilità e di fare conoscenza con un nuovo tipo di calcolo, relativo a eventi che possono essere scomposti in singoli eventi, anche del tutto indipendenti tra loro.   Le difficoltà aumentano un poco, ma la preparazione che abbiamo dovrebbe essere ormai sufficiente a superarle. Nessuna formula o concetto astruso, ma una serie di trasformazioni che vanno seguite e comprese con particolare attenzione. Questo cambio di rotta impone anche un cambiamento di punto di vista. Finora abbiamo calcolato una probabilità finale considerando e "sommando" le probabilità di ogni strada che può portare all'accadimento di un certo evento. Adesso, invece, dobbiamo, per semplicità, considerare assodata la strada più probabile, che si porta, comunque, dietro il valore della sua probabilità, e calcolare come le probabilità di ogni pezzo di strada (considerato  stabilito) si combinano per determinare la probabilità finale.

Sembra un discorso particolarmente difficile e nel prossimo articolo cercheremo di spiegare tutta la sequela di azioni da fare,con particolare attenzione, arricchendola di dettagli e di esempi. Cercheremo anche di spiegare, molto meglio, in cosa consiste questo cambio di "marcia". Non spaventatevi, però: è solo una questione di tecnica operativa e niente di più

Vedremo che, dopo questa ulteriore fatica, finalmente la parola “elettrodinamica”  acquisterà una sua logica. Ma dobbiamo attendere e avere pazienza…

Chi vuole fermarsi, ha già imparato molto, ma vi invito caldamente a continuare a seguirmi. Al limite, mi chiederete tutti i chiarimenti del caso!