Per una trattazione completa dell'Elettrodinamica Quantistica (QED), si consiglia di leggere il relativo approfondimento, in cui è stato inserito anche il presente articolo

 

In questo articolo ci dedichiamo all’esperimento della doppia fenditura e ci accorgiamo che è diventato veramente banale e intuitivo. La QED lo descrive in modo perfetto e … “logico”. Anche la parte più assurda ha una "spiegazione" più che convincente.

Con tutto quello che abbiamo imparato finora (soprattutto, le regole di calcolo della probabilità di un evento attraverso le frecce associate alle traiettorie percorribili da un fotone), non è  difficile riprendere il celebre esperimento della doppia fenditura, su cui tanto a lungo abbiamo discusso, e descriverlo con grande naturalezza. Ci sembrerà più che ovvio. Addirittura, tenendo conto della separazione degli eventi in passi successivi, si può anche dare una risposta alla parte più assurda, ossia quella relativa al guardare o non guardare da dove passa il fotone. Vale proprio la pena descriverlo nuovamente, cercando di afferrare bene non tanto le operazioni (ormai banali) ma i concetti che ne derivano, soprattutto l’ultimo.

Prepariamo l’esperimento con la sorgente S e la parete con i due fori A e B, distanti tra loro pochi millimetri, e il rivelatore R. Poniamo il foro A proprio nella direzione SR (ma potevamo anche cambiare la posizione dei fori).  La cosa veramente importante è che i fori siano molto piccoli. Perché? Dovreste ricordarvelo: se i fori sono piccoli le traiettorie che li attraversano danno luogo a una combinazione delle  frecce di ampiezza comparabile, indipendentemente dalla lunghezza della traiettoria seguita e dal tempo impiegato a percorrerla. In altre parole, la traiettoria SAR  ha la stessa probabilità finale di SBR, malgrado la seconda sia decisamente più lunga. Ricordiamo, per avere un’idea più chiara delle grandezze in gioco, che se i due fori distassero un metro, il loro diametro dovrebbe essere di un decimo di millimetro…

Partendo da questa verità, non è quindi difficile superare la prima apparente assurdità della situazione: se chiudo A ottengo un certo risultato su R. Se chiudo B ottengo lo stesso identico risultato. In numeri (come esempio): se S invia cento fotoni, uno solo passa attraverso A (con B chiuso) e arriva su R (facendo “tic”). Se chiudo A, e mando altri cento fotoni, R farà nuovamente “tic” una sola volta, confermandoci che il percorso SBR ha la stessa probabilità di SAR. Questo è un risultato già abbastanza assurdo per la vita normale, ma sappiamo spiegarlo benissimo con un fascio di traiettorie molto strette.

Accettiamo quindi che la probabilità di arrivare su R da S, sia attraverso A che B, sia la stessa, ad esempio l’1%. Apriamo, ora, entrambi fori. Se ragionassimo come siamo abituati a fare, dovremmo dire che, se lanciamo 100 fotoni da S, ne arrivano 2 su R: uno attraverso A e uno attraverso B. Questa è la nostra logica. Chi non ha letto quanto scritto finora si stupirebbe non poco del fatto che, invece, il numero di fotoni che giunge su R varia da un valore minimo di zero a uno massimo di 4.

Noi, però, siamo già abbastanza preparati da sapere che non possiamo sommare le probabilità nel modo più banale, ossia 1 + 1 = 2! Qual è l’evento che devo studiare? Il fotone parte da S e arriva in R con due percorsi alternativi (esso è verificato sia se il fotone passa da A sia se passa da B). Alternativi? Ma allora sappiamo benissimo come fare: dobbiamo disegnare le ampiezze di probabilità per le due traiettorie possibili (attraverso A e attraverso B), fare girare il cronometro, che gira di più per il percorso più lungo, e sommarle vettorialmente. La probabilità finale è il quadrato dell’ampiezza finale.

Tutto dipende, quindi, dalla distanza tra i fori, ossia dalla differenza di percorso effettuato nelle due traiettorie alternative, ossia, da quanto ha girato la lancetta nei due casi. Per una certa distanza tra i fori potremmo avere che le due frecce vanno nello stesso verso e quindi prima sommiamo le frecce: 1 + 1 = 2 e poi eseguiamo il quadrato, che mi dà una probabilità finale di 4 (il 4%). Per un’altra distanza tra i fori, potremmo avere che le due frecce vanno in verso opposto, ossia 1- 1 = 0, il cui quadrato resta 0 (lo 0%).

E’ la stessa cosa che abbiamo trovato con la doppia riflessione sulla lastra di vetro sul rivelatore R1, niente di più e niente di meno. Non sappiamo assolutamente perché il fotone decida di passare da A o da B, ma sappiamo benissimo calcolare la probabilità di ogni traiettoria possibile del singolo fotone e combinarle in modo da ottenere la probabilità finale dell’evento.

Ovviamente, invece di spostare i fori, potremmo spostare il rivelatore R e troveremmo che, mentre si muove, la luce passa da un massimo (4%) a un minimo (0%), in relazione alla rotazione della lancetta, ossia alla distanza totale percorsa nelle due strade alternative. Questo fenomeno, che sappiamo trattare benissimo con le nostre frecce, è seguito pari pari dalla Natura e viene chiamato “normalmente” interferenza.

Quanto detto lo illustriamo in Fig. 46

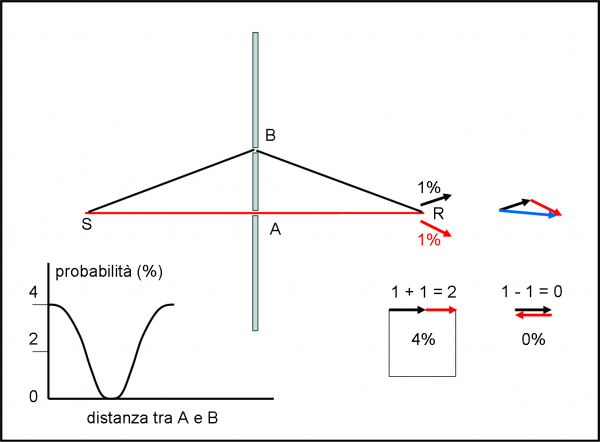
Se, invece, apriamo uno alla volta i fori, abbiamo due eventi separati: uno che dice di andare da S a R attraverso A e un altro che dice di andare da S a R attraverso B. Non vi sono alternative e quindi la freccia che arriva in R è una e una sola per ogni evento. Chiudendo A e aprendo B, la sola traiettoria possibile è SBR. Chiudendo B, l’unica traiettoria possibile è SAR.  Non abbiamo un evento con due alternative, ma due eventi, ciascuno senza alternative. Non dobbiamo quindi sommare vettorialmente le frecce, ma sommare “brutalmente” le percentuali dei due eventi, così come abbiamo fatto sommando le percentuali trovate nel rivelatore che riceve la doppia riflessione e in quello che riceve la trasmissione attraverso la lamina di vetro.

Ogni evento ha, come già detto, la probabilità dell’1%. I due eventi sono separati e quindi se vogliamo sapere quanti fotoni arrivano su R, passando da A o da B, dobbiamo sommare “brutalmente” le due probabilità e otteniamo 1 + 1 = 2. Non andiamo contro la QED e la differenza del risultato dipende solo da come è definito l’evento. Impariamo bene questo concetto e analizziamo sempre con molta attenzione le caratteristiche dell’evento di cui vogliamo calcolare le probabilità di riuscita.

Esistono ancora problemi di comprensione tra il fatto che, quando il foro è singolo, il fotone si comporta come “vera” particella, e il fatto che, quando i fori sono due, il fotone si comporta come un’onda? Un’onda che nei due fori dà luogo a due onde che interferiscono tra loro. No, direi proprio di no. Ormai nella logica della QED questo è un risultato ovvio e comprensibilissimo.

E’ bastato pensare un fotone come un insieme di particelle virtuali che possono essere ovunque, o, meglio ancora, trattare il comportamento di un fotone come un insieme di traiettorie ognuna con la propria ampiezza di probabilità di soddisfare un certo evento

Se questo fatto non vi risulta banale e ovvio, vi consiglio di ricominciare da capo la QED… Ma spero che non capiti a nessuno!

Ridendo e scherzando abbiamo descritto l’interferenza e abbiamo visto perché dipende dalla separazione dei fori o dal punto in  cui si mette il rivelatore. Abbiamo dimostrato che le particelle (e i fotoni lo sono perché fanno “tic” sul rivelatore) vanno trattate attraverso ampiezze di probabilità per ottenere i risultati che segue la Natura. Nessuna vera dualità particella-onda, ma solo freccia e cronometro… Mi raccomando, stiamo sempre bene attenti a definire perfettamente l’evento!

Fin qui nessun problema direi… Il bello viene adesso. Comunque, vedremo che la QED riesce anche a spiegare “a modo suo” il famoso fotone dispettoso che diventa particella se lo guardi e rimane onda se non lo guardi. Ossia il nocciolo di fondo di tutta la MQ. E non lo fa assolutamente dando all’osservatore e al suo cervello una capacità miracolosa…

Proseguiamo allora con molta calma. L’esperimento rimane tale e quale a prima, ma adesso al posto dei fori A e B, usiamo due fori muniti di un rivelatore incorporato. Ossia un qualcosa che, in pratica, ci dice se il fotone passa attraverso quel foro. Non dobbiamo confonderci: noi trattiamo nella QED il fotone come un insieme di ampiezze di probabilità che, in questo senso, possono passare sia da A che da B e combinarsi assieme. Tuttavia, il fotone resta una particella e in  realtà o passa da A o passa da B, non può passare mezzo da A e mezzo da B o cose del genere. Quelli che arrivano in R devono essere passati da qualche parte come particelle. Siamo solo noi, che non sapendo come spiegare la scelta dei fotoni, li abbiamo trattati e descritti come ampiezze di probabilità. L’importante è che facendo così riusciamo a descrivere perfettamente la Natura!

Torniamo ai due fori “intelligenti” o -molto meglio- capaci di registrare in qualche modo se un fotone passa o no attraverso di lui (basta la tecnologia e non l’intelligenza…e già la MQ cambia un po’ la sua visione troppo legata all’uomo… ma ci torneremo sopra, ovviamente). Il risultato lo sappiamo bene: l’interferenza scompare e il rivelatore R si comporta come ci saremmo aspettati fin dall’inizio: 1 + 1 = 2 e non certo 0 oppure 4!

Una soluzione apparentemente e normalmente NORMALE che, adesso, non ci soddisfa più e ci mette in crisi! Se ci sta succedendo questo, vuol dire che siamo entrati nel mondo di Alice e stiamo pensando come lei: il normale diventa assurdo e l’assurdo diventa normale.

Non sembra, però, che vi sia nessuna regola descritta finora che possa spiegare questo strano comportamento. La normalità del risultato sta distruggendo le nostre certezze basate sulla QED. Ma ne siamo proprio sicuri? Come abbiamo già detto varie volte, dobbiamo essere sempre certi di aver definito perfettamente l’evento. Due eventi uguali devono dare risultati uguali. A noi sembra che aggiungere i fori “intelligenti” non abbia cambiato l’evento e, invece, è proprio così. Seguiamo bene il ragionamento perché è veramente fondamentale (anche se rispecchia pari pari quanto detto poche righe sopra)

Per essere sicuri che l’evento non sia cambiato dobbiamo analizzare molto bene le condizioni iniziali e finali in modo da accorgerci se esse sono variate. Se così fosse, tutto l’evento sarebbe stato modificato e il risultato potrebbe benissimo essere diverso.

Descriviamo bene l’evento senza fori “intelligenti”. Cosa dice esattamente? Molto semplice: la luce parte da S, può passare da A o da B, e il rivelatore R fa “tic”. L’unica variazione di condizioni che avviene durante l’esperimento è il “tic” del rivelatore. O lo fa o non lo fa. Noi non possiamo sapere come si è mossa effettivamente la luce e quindi la descrizione data dalla QED ci dimostra che vi deve essere interferenza e la Natura lo conferma.

Quando inseriamo i fori “intelligenti”, noi cambiamo profondamente l’evento che adesso diventa: la luce parte da S, A o B registrano il passaggio del fotone, il rivelatore R fa “tic”. Non ditemi che è la stessa cosa di prima! Vi sono ben tre condizioni: la registrazione effettuata del foro A, quella del foro B e il solito tic di R (che c’era anche prima). L’evento non è più lo stesso!

Questo evento è in realtà scomponibile in due eventi distinti e completi: (1) la luce parte da S, passa  da A e fa tic in R; (2) la luce parte da S, passa da B e fa tic in R. Due eventi completamente separati, che vanno trattati in modo diverso secondo le regole imparate.

Scomponiamo (1) in due passi: da S ad A e da A a R. Dobbiamo farlo per studiarlo adeguatamente perché in A cambiano le condizioni, così come capitava nell’esperimento della doppia riflessione e in altri esempi. La freccia che arriva in A deve essere MOLTIPLICATA con quella che va da A a R. Tuttavia, questo evento è perfettamente uguale a quello con solo A aperto. Il foro intelligente non cambia la probabilità finale, ma implica solo che l’evento completo (da S a R) deve essere spezzato in due eventi separati.

Ripetiamo ancora il concetto. L’evento che porta all’interferenza dice solo e soltanto: parti da S e arriva in R facendo “tic”. Esso, per come è formulato, ammette due strade alternative, il passaggio da A o da B. Basta allora che faccia la somma vettoriale finale sulle frecce. La QED e le sue regole ce lo impongono! L’evento invece che vuole un  passaggio registrato da A e un  “tic” in  R, ma che vuole anche un passaggio in B e un “tic” in R, non è un  singolo evento. Infatti, se abbiamo un passaggio da A non esiste strada alternativa: passare da A è l’unica strada possibile. Se, contemporaneamente, vogliamo che l’evento ammetta la possibilità del passaggio da B dobbiamo concludere che è una cosa del tutto diversa, dato che l’unica strada possibile è passare da B. L’evento non è uno solo, ma è composto da due eventi del tutto diversi.

Trattiamoli allora come tali. E’ facilissimo. (1) ci dice che se la luce può passare solo da A e arrivare in R, la probabilità finale è dell’1%, tale e quale al caso di un unico foro aperto. (2) ci dice la stessa identica cosa: la luce deve passare da B e arrivare in R. Nuovamente uguale al caso di un unico foro aperto. Anche la sua probabilità finale e l’1%. I due percorsi non sono vie alternative di un solo evento, ma sono due eventi complementari: o se ne segue uno o se ne segue un altro, tale e quale al caso della lastra con doppia riflessione e i due rivelatori messi in R1 (che raccoglie la luce riflessa) e in R2 (che riceve la luce trasmessa attraverso il vetro). Cosa dovevamo fare in quel caso: sommare tra di loro le probabilità dei due eventi, dato che la luce o fa una cosa o fa l’altra. Lo stesso capita adesso: anche se il rivelatore è adesso sempre lo stesso R, devo comunque sommare le percentuali dei due eventi differenti, dato che o capita (1) o capita (2).

Ripeto ancora, non fatevi ingannare dal fatto che il rivelatore rimanga sempre R. In parole povere, R fa un doppio lavoro: registra la probabilità dell’evento (1) e quello dell’evento (2), proprio come se avessimo fatto coincidere R₁ e R₂ nel caso della doppia riflessione. Non confondiamo nemmeno la situazione con quella delle Fig. 43 e 44. Nel caso attuale i due eventi non sono strade indipendenti che verificano lo stesso evento, ma due eventi completamente separati (li avevamo chiamati complementari), dato che in un caso è obbligatorio il passaggio da A e nell’altro il passaggio da B. Nel caso delle sorgenti X e Y, invece, volevamo verificare l’evento, definito così: partendo da X e da Y, due fotoni arrivano in A e in B . le strade XA e YB andavano moltiplicate perché erano vie indipendenti ma entrambe necessarie affinché l’evento si avverasse. Lo stesso capitava per YA e XB. Le due frecce ottenute da queste due azioni indipendenti, ma plausibili, si ricavavano attraverso la moltiplicazione e le loro ampiezze dovevano poi essere combinate con la regola della somma vettoriale, dato che erano vie alternative per l’attuazione dell’evento completo.

Pensiamo  anche a un problema aggiuntivo, ma facilmente risolvibile: “E se i fori non fossero tanto intelligenti? Ossia, se ogni tanto individuassero il passaggio e ogni tanto se lo “perdessero”?”. Ebbene, la soluzione è veramente ovvia: a mano a mano che scende la credibilità dei due fori  “intelligenti” l’interferenza aumenta e si avvicina al valore massimo che si ha con fori del tutto “ignoranti”! Insomma, si ha un mix delle due soluzioni, in quanto in certi casi vale l’evento unico e in altri l’evento spezzato in  due. E’ vero o non è vero che la QED è, in fondo, logicissima?

Questo articolo ci ha detto due cose molto importanti e fondamentali. Innanzitutto ci ha insegnato a stare molto attenti a definire un evento. Variazioni che sembrerebbero non incidere lo stravolgono completamente e lo spezzano addirittura in due eventi. Come conseguenza, abbiamo anche “capito” perché se i fori sono intelligenti il risultato è diverso. Non perché andiamo a curiosare quello che non dovremmo vedere, ma solo e soltanto perché abbiamo cambiato drasticamente l’evento, spezzandolo in due eventi del tutto separati. Potremmo anche  non voler sapere da che parte è passato il fotone, ma se esiste qualcosa (i rivelatori vicini ai fori) che potrebbe dirci da che parte è passato, vale, comunque, la separazione degli eventi. Si può anche dire che gli "stati" finali sono differenti, dato che adesso le condizioni finali sono, praticamente, distinguibili tra loro....

Attenzione! Questo ragionamento non risolve certo il problema di fondo della MQ e che tanto ha fatto e  fa ancora discutere gli esperti. Chi e che cosa deve intromettersi sul percorso di un fotone perché lui diventi veramente una particella? Sembrerebbe che basti cambiare la struttura dell’evento e il gioco è fatto. Sì, ma come si cambia questa struttura? Se noi non  potessimo verificare la diversità, la presenza del foro intelligente non servirebbe a niente. Quindi sembrerebbe che la nostra presenza ottica o uditiva (o quello che volete) sia sempre necessaria. E se ci fosse un gattino ad ascoltare il tic? O magari solo un’altra particella curiosa? O, molto più semplicemente, un qualcosa di esterno che si intromette in un fenomeno circoscritto e chiuso in se stesso?

Quest’ultima è la soluzione che preferisco… La particella si muove attraverso ampiezze di probabilità quando agisce in un sistema chiuso. Non appena viene a contatto con qualcosa che appartiene al mondo esterno (foro intelligente, occhio dell’uomo o anche quello del gatto) l’evento si modifica e l’onda collassa (tanto per usare il linguaggio più tipico della MQ). In parole più semplici, però, possiamo anche dire che se qualcosa dimostra che la particella fotone passa in un certo punto, tutti gli altri fotoni virtuali spariscono (e, in qualche modo, cadiamo nelle particelle entangled …).

Tuttavia, non possiamo seguire questa strada (adesso) e lascio a voi i confronti tra i vari modi di descrivere la MQ. Noi dobbiamo andare avanti con la QED che, adesso, utilizzando le poche regole definite finora (che sono perfettamente confermate dalla Natura), ci permette di descrivere  tutti i fenomeni della fisica, al di fuori della gravità e di ciò che capita dentro al nucleo atomico. Vi sembra poco? Direi proprio di no, dato che anche la chimica, la biologia e molto altro ancora si basano solo sulle interazioni tra luce e materia.  Accontentiamoci e vedrete che non saremo delusi!

Devo essere sincero fino in fondo. Le cose cominceranno a diventare un po’ più difficili e saremo obbligati a fare riferimento a qualche formula che non potremo, però, ricavare, dato che bisognerebbe entrare nella QED e nelle sue espressioni matematiche. Questo sarebbe troppo, anche per me… ve lo assicuro. Prenderemo per buone alcune conclusioni, ma capiremo cosa vogliono significare (questo è l’importante). Introdurremo anche il tempo, anzi lo spazio-tempo e la trattazione ci porterà a concetti e a dimensioni difficilmente visibili con occhi normali. Abbiamo i mezzi per parlare e capire il linguaggio di Alice, ma l’impegno non sarà trascurabile.

Un consiglio:  andate a riguardare l’articolo elementare che avevo scritto come aggiunta al libro di Rosetta (QUI), senza curarvi dell’espansione.  Potrebbe venire utile ai meno esperti.