I numeri interi e i loro multipli, interpretati come onde che si propagano verso l'infinito; un modo inconsueto di riflettere sulle proprietà dei numeri interi consecutivi entro un intervallo di valori, il tentativo di capire cosa accade lontano studiando ciò che è vicino. Una specie di surfing sulla cresta delle onde, sul loro affastellarsi, morire e rinascere.

 

Una rappresentazione ondulatoria dei numeri interi.

Generalmente, parlando di numeri interi, la prima cosa che viene in mente per rappresentarli è una serie di punti equispaziati sopra ad un asse orizzontale.  Ma come potremmo immaginare di segnare questi punti in modo semplice ed automatico? Ebbene potremmo pensare di associarli ad una funzione periodica, un' onda, come una clicloide, che abbia un periodo rigorosamente uguale all'unità.

Ecco come l'onda di periodo 1 ( che possiamo chiamare O₁ ) segna per noi i numeri interi sull'asse.

Tutti i punti in cui l'onda ricomincia , formando una cuspide  ( ricordiamo ai lettori che  la "cuspide" è un punto particolare della curva in cui i limiti sinistro e destro del rapporto incrementale assumono valori infiniti, di segno opposto) , indicano un numero divisibile per il modulo dell' onda, che in questo caso vale 1. Quindi si parla di tutti i numeri interi.

Ma se volessimo individuare , ad esempio, tutti i numeri pari? Cioè tutti i numeri divisibili per 2?

Basta immaginare la progressione dell'onda O₂, di periodo doppio. Eccola:

Questo è solo il primo periodo, poi proseguiamo con tutti i multipli, così:

Vediamo che questa onda O₂ “scavalca” il numero 3 , raggiunto solo dall'onda O₁ che, peraltro, passa per qualsiasi numero.

Il fatto che il 3 non sia multiplo di 2 lo pone nella condizione di essere il primo numero di una nuova serie, formata da 3 e da tutti i multipli di 3. Il tre è un numero “primo” e avrà associata l'onda O₃.

Vediamo la nuova onda nella figura seguente, sovrapposta a quelle già disegnate.

Ci siamo fermati al primo multiplo di tre, ossia il 6.

Non è per caso.

Incidentalmente notiamo che il primo numero per il quale non passa alcuna onda, oltre alla O1, è il numero 5. Si tratta quindi di un altro numero primo. Ma la cosa che più ci interessa in questo momento è la constatazione che in corrispondenza del 6 tutte le onde formano una cuspide, contemporaneamente.

Questo implica che tutte le onde ricominceranno il loro ciclo nelle medesime condizioni in cui si trovavano alla partenza, in corrispoondenza del punto 0. Il punto 6 è equivalente al punto zero.

Il riallineamento di tutte le onde si verifica precisamente in corrispondenza del punto che rappresenta il minimo comune multiplo dei loro moduli. Nel nostro caso il mcm tra 1 2 e 3 , appunto 6.

Questa animazione ci mostra come la rilocazione di una parte del fascio di onde, un tassello ”unitario” che viene riposizionato dalla coda della catena alla sua testa non produca alcun cambiamento, dato che il contenuto del frammento spostato non varia, il numero totale di cuspidi nell'intervallo complessivo, il loro numero rimane costante ad ogni mossa.

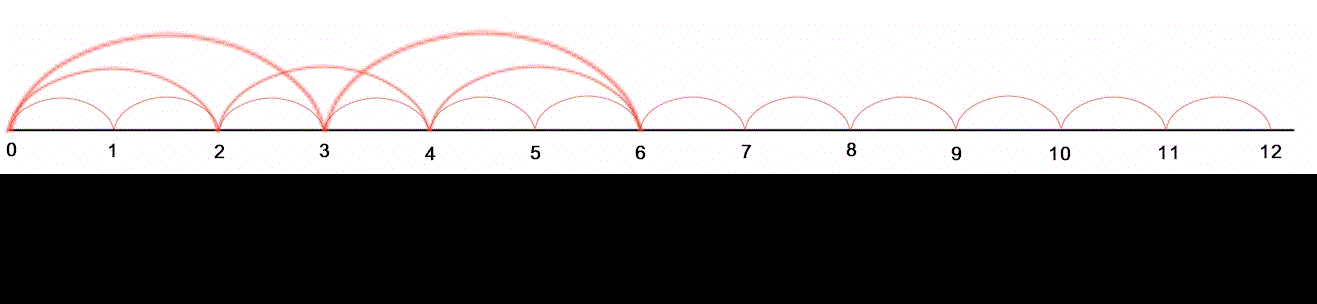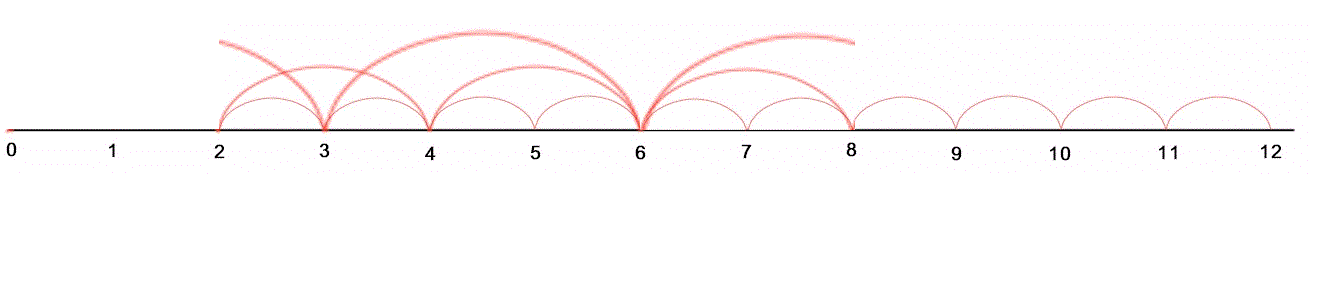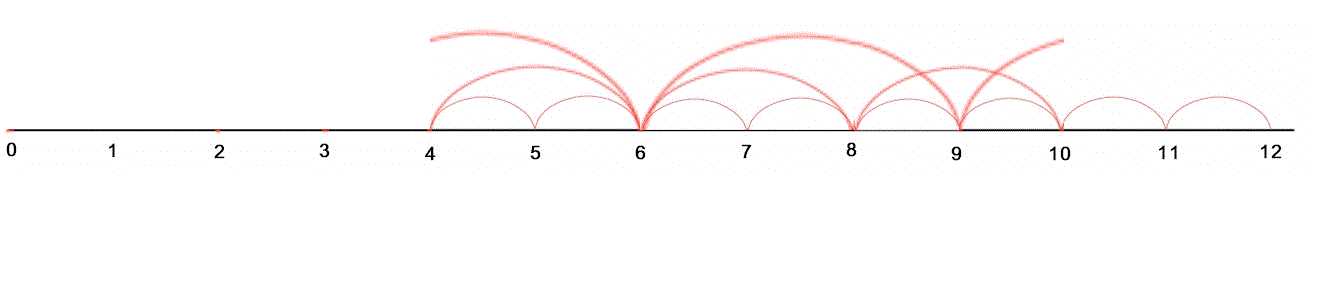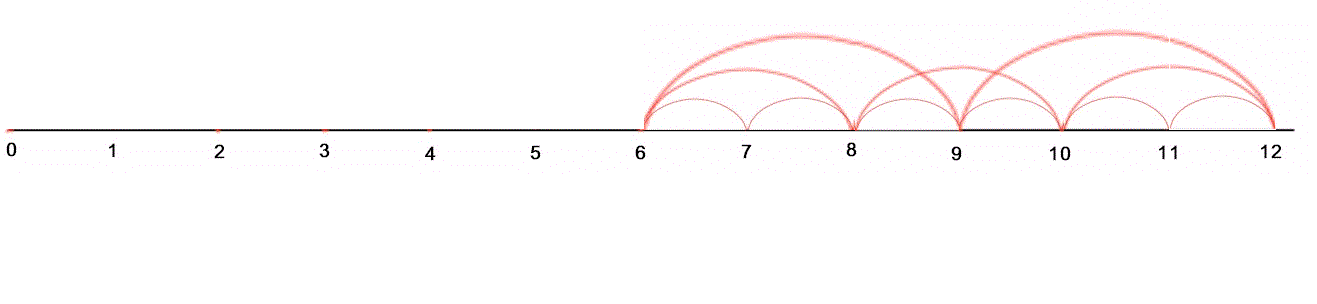
Se ci concentriamo sul primo intervallo da 1 a 3, vediamo che le onde si completano tutte una prima volta, rispettivamente nei punti 1 2 e 3. A ciascuna di esse corrisponde un divisore specifico.

Il prodotto dei tre numeri in sequenza è divisibile per i tre numeri 1 2 3 che costituiscono i divisori.

In altri termini il prodotto dei numeri di questo intervallo è divisibile per il prodotto 1*2*3 che si chiama "Fattoriale di tre" e si indica con 3 seguito dal punto esclamativo, così:  3!

Ovviamente, in questo intervallo, il risultato del rapporto vale 1.

Domandiamoci ora se questa divisibilità permane scegliendo un diverso punto di partenza per la sequenza dei tre numeri. Ossia invece di 1,2,3 esaminiamo la sequenza 2,3,4. Il prodotto di questi tre numeri consecutivi sarà sempre divisibile per 3! oppure no?

E se analizziamo la sequenza 3,4,5 ? o una qualsiasi altra sequenza p, p+1, p+2, con p intero, di qualsiasi valore ?

Osserviamo questa seconda animazione.

Spostando l'intervallo varia la distribuzione delle cuspidi, ma non il loro numero, ne abbiamo sempre una per ciascun divisore.

Questo significa che la divisibilita del prodotto dei numeri, in questo nuovo intervallo, coincide con la divisibilità riscontrata nell'intervallo precedente: vale sempre 3! ossia il fattoriale di tre.

Ovviamente , mutando i valori in gioco negli intervalli 2,3,4 e 3,4,5 , il risultato della divisione non sarà più 1, ma risulterà via via crescente.

Considerando le onde O₁ O₂ O₃ abbiamo individuato una trama precisa, una specie di “impronta digitale” nell'intervallo che si delinea tra il punto 1 e il punto 6 (mcm di 1,2,3) e si ripete all'infinito.

Ma 6 , oltre ad essere il mcm, è contemporaneamente il fattoriale 3!

Certo, ma solo perché, nel caso che stiamo esaminando, tra i numeri 1 2 3 nessuno è multiplo di un altro. Se aggiungessimo il 4, ( multiplo di 2) disegnando l'onda O₄, il mcm sarebbe 12 , mentre il fattoriale 4! sarebbe 1*2*3*4 =  24.

Insomma, in questo quartetto di onde, la O₄ “contiene” la O₂ , allora nel minimo comune multiplo la O₂ è eccedente, mentre nel fattoriale va conteggiata.

Ecco l'aspetto della configurazione base, da 1 al mcm, nel caso di un intervallo di numeri da 1 a 4:

Vediamo molto distintamente i numeri che sono stati raggiunti solo dall'onda O₁ e da nessuna altra (quindi non divisibili per 2, 3, 4) Essi sono i numeri primi 5, 7, 11, che saranno i punti di innesco di nuove onde.

Se passiamo dalla sequenza iniziale , ossia l'intervallo 1 2 3 4 , alla sequenza  successiva   2,3,4,5 ...

vediamo come, pur variando la posizione relativa delle cuspidi, per ogni onda esse siano sempre in numero tale da garantire la divisibilità, come nel caso di prima.

Se saltiamo, per il nostro confronto ad un punto più distante dall'origine, come 8,9, 10, 11 …

osserviamo che la prima cuspide è quella di O₄, seguita da O₃ e infine da O₂, quindi una disposizione che è l'esatto opposto di quella del primo intervallo, eppure, ai fini della divisibilità nulla è cambiato, tutte e tre le onde transitano nel nuovo intervallo e determinano con la loro presenza la medesima divisibilità del prodotto dei numeri dell'intervallo per 4!.

In questo schema, l' ampiezza dell'intervallo ( numero k di numeri interi consecutivi) e il suo punto di partenza (valore del numero iniziale p ) non entrano in gioco nel determinare la divisibilità del prodotto dei numeri dell'intervallo, che resta costantemente uguale a k! , quella stessa divisibilità valida per l'intervallo base, che inizia con 1.

Un esempio numerico di sequenza di 3 numeri interi , dove ben due dei tre numeri sono numeri primi, potrebbe essere 11,12,13; il loro prodotto è divisibile per 3! e dà come risultato 286.

I numeri primi non vengono toccati da alcuna onda , salvo O₁ ,mentre nel 12 confluiscono le onde O₂ e O₃

Un esempio di 4 numeri, di cui due primi è 101,102,103,104 ; il loro prodotto è divisibile 4! e dà come risultato la bellezza di 4.598.126. Anche in questo caso per i due numeri primi ( 101 e 103), cosidetti numeri primi gemelli perché sono semplicemente separati dal numero pari intermedio, passa solo l'onda O₁. L'onda O₂ passa per 102 e 104, l'onda O₃ passa per 102 e l'onda O₄ passa per 104 ( ma non per 102). Come si vede ogni onda trova spazio nell'intervallo, condividendo eventualmente il numero toccato con  altre onde.

Potremmo dire che il modello costituito dalla configurazione visibile nell' intervallo formato dai numeri da 1 al mcm (dei numeri da 1 a k) , fissa l'identità del fascio di onde, una specie di DNA che determina la divisibilità di tutte le sequenze formate da k numeri consecutivi, comunque dislocate

Finalino

Un rinomato Professore di Astrofisica mi ha fatto notare che la figura ripetitiva che ho proposto fino allo sfinimento, viene anche usata (sostituendo alle  mie cicloidi delle semicirconferenze) per dimostrare che pigreco vale DUE. In effetti sarebbe una bella comodità per tutti.

Il meccanismo surrettizio della dimostrazione consiste nella suggestione che, aumentando il numero delle semicirconferenze e rendendole sempre più minuscole,  il limite della lunghezza della semicirconferenza debba tendere al diametro. Il rapporto tra semicirconferenza e diametro varrà così 1.  Dato che la semicirconferenza vale pi*r   e  il diametro vale 2* r ,  per qualsiasi valore di r , si deduce che pigreco vale 2.

Un giochino niente male , come quello che abbiamo visto qualche quiz fa, parlando di  una scala che "diventava" una retta.

Ebbene, cari lettori, lasciatemi dire che...

Ci sono cose che non mutano, anche se ci si spinge nell'infinito o nell'infinitesimo. Un'onda è sempre uguale a se stessa, anche dopo un numero infinito di cicli periodici e il "rapporto di forma " di una figura resta ciò che è, anche se riduciamo l'ingrandimento ad un infinitesimo.

Quindi, non fatevi imbrogliare ....

Se state per cedere alla tentazione, ricordatevi questa figura:

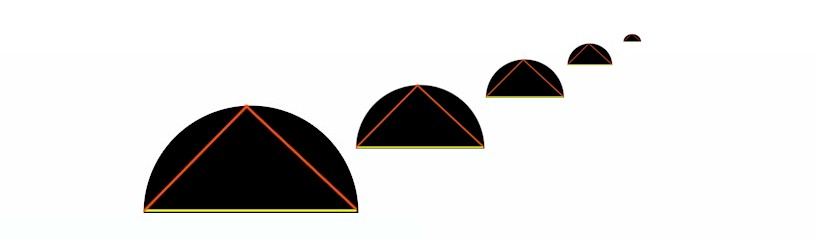
 Per piccolo che sia il raggio, la spezzata dei due lati è sempre più grande della base, ossia vale sempre 2√2 r > 2r.