Categorie: Meccanica Celeste Sistema Solare
Tags: conservazione dell'energia energia orbitale moto circolare uniforme moto orbitale riduzione massa solare teorema del viriale terza legge Keplero
Scritto da: Vincenzo Zappalà
Commenti:0
E se il Sole perdesse metà della sua massa? **
Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.
La domanda è semplicissima: “Cosa succederebbe alla Terra e alla sua orbita se, improvvisamente, il Sole riducesse la sua massa alla metà di quella attuale?” Notate che quando dico improvvisamente dico anche immediatamente, come se fosse stato toccato dalla bacchetta magica di una fata.
Il problema ha tutti gli asterischi che volete, dato che può essere risolto in pochi secondi, ma anche attraverso lunghi e laboriosi calcoli. E le risposte potrebbero anche essere molto diverse tra loro…
Tuttavia, non vogliamo introdurre nessun problema di dinamica complessa e/o relativistica, né –tantomeno- innescare sconvolgimenti fisici del Sistema Solare. Vuole essere solo un “gioco” legato a una soluzione istantanea. Poi, ognuno, può vederci i risvolti più reconditi, non ultimo il legame con i gravitoni che potrebbero ritardare gli effetti della riduzione di massa solare.
Facciamo un po’ di ripasso di dinamica orbitale elementare…
Calcoliamo, innanzitutto, la velocità orbitale di un oggetto che rivolve attorno al Sole su un’orbita circolare (come la Terra, in ottima approssimazione). Vi sono vari metodi, ma noi utilizziamo, ad esempio, la terza legge di Keplero.
Innanzitutto, dato che il moto è circolare e uniforme, deve valere la relazione ben conosciuta :
v = 2πa/P …. (1)
Non abbiamo fatto altro che scrivere una proporzione, imponendo che se la Terra si muove di moto circolare con velocità costante di tot metri in tot secondi (v) deve anche percorrere l’intera circonferenza in un periodo P, dove a è il semiasse maggiore dell’orbita che coincide con il raggio della circonferenza.
Possiamo comunque scrivere, in modo indipendente, la terza legge di Keplero che dice :
P2 = 4π2a3/GM …. (2)
Basta, ora, sostituire nella (1) il periodo P ricavato dalla (2) e otteniamo:
v = 2πa/2aπ(a/GM)1/2 = (GM/a)1/2 …. (3)
Questa è la velocità orbitale in ogni punto di una traiettoria circolare. Essa dipende ovviamente dalla massa del Sole (M) e dalla distanza, ma è un entità fisica acquisita che comporta un’energia cinetica della Terra che può essere scritta:
K = ½ mv2
e che è, ovviamente, una costante.
In ogni punto della sua orbita l’energia totale del sistema deve conservarsi. All'energia cinetica va quindi aggiunta l’energia potenziale che dipende dalla massa del Sole e dalla sua distanza. In ogni punto dell’orbita deve valere:
E = ½ mv2 – GMm/a …. (4)
Insomma, il solito vecchio e ben noto equilibrio tra energia cinetica ed energia potenziale.
Cosa succederebbe se, improvvisamente, eliminassimo il Sole? Sarebbe un po’ come tagliare la corda a una pallina che viene fatta girare velocemente attorno a noi. Beh… nessun mistero: la pallina se ne andrebbe per la tangente in balia della sua sola energia cinetica. Nell’istante esatto del taglio della corda la velocità della pallina sarebbe comunque uguale alla “vecchia” v.
La stessa cosa deve perciò capitare anche alla Terra che si vede sparire ISTANTANEAMENTE il Sole. Possiamo perciò concludere che nell’istante della sparizione la velocità v si mantiene.
Estrapoliamo il discorso anche al caso in cui il Sole non sparisca del tutto, ma riduca la sua massa a metà di quella normale. Anche in questo caso potremmo dire che la velocità v si mantiene.
Tuttavia, l’equazione (4) deve cambiare almeno una sua parte, quella dovuta all’energia potenziale. Essa dipende dalla massa M del Sole e se lei diminuisce deve immediatamente variare anche l’energia. Nel caso di una massa pari a M/2 la (4) diventa:
E = ½ mv2 – GMm/2a …. (5)
Perfetto… però, non possiamo certo dimenticare che la velocità v è espressa dalla relazione (3). Nessuno ci vieta di inserirla nella (5), che diventa:
E = ½ m ((GM/a)1/2)2 – GMm/2a
e ancora:
E = GMm/2a - GMm/2a
Accidenti, quella che abbiamo scritto è un’equazione che porta i due membri ad annullarsi, ossia alla relazione “fisica”:
E = 0
Cosa significa tutto ciò? Che l’energia orbitale, nell’istante in cui il Sole viene dimezzato improvvisamente, diventa ZERO. Ma, sappiamo benissimo che un’orbita che ha energia nulla non è altro che una parabola. La Terra perciò assume istantaneamente una traiettoria parabolica.
Se cambiassimo la massa del Sole di un fattore diverso avremmo soluzioni analoghe e altrettanto interessanti. Se diventasse solo un po’ più piccolo, ossia avesse una massa finale di 2/3 di quella originale, avremmo:
E = GMm/2a - 2GMm/3a = (3GMm – 4 GMm)/6a = - GMm/6a < 0
Il che ci direbbe che l’orbita istantanea diventa un’ellisse, dato che l’energia orbitale è negativa
Se, invece il Sole si riducesse a 1/3 della massa originaria, avremmo:
E = GMm/2a – GMm/3a = (3GMm – 2GMm)/6a = GMm/6a > 0
Ossia, avremmo un’orbita iperbolica.
Ah…, tra parentesi, tutto ciò che abbiamo detto e, in particolare, la “creazione” istantanea e momentanea dell’orbita parabolica ci riporta, tanto per cambiare, al teorema del viriale. Un “prezzemolo” molto più consistente di tanti altri che sembrano avere un’importanza solo… decorativa.
Studiamo con maggiore attenzione ciò che capiterebbe all'orbita terrestre se la massa del Sole dovesse istantaneamente ridursi (trascurando tutti gli effetti di tipo fisico). Il "gioco" è abbastanza interessante. Tuttavia, non pretendiamo di andare ancora oltre... un bel gioco dura poco!
Torniamo, quindi, al nostro Sole che ha deciso di perdere massa improvvisamente e studiamo meglio cosa succede all’orbita della Terra supposta circolare. Introduciamo attentamente le grandezze in gioco.
Un oggetto che si trova in una certa posizione, rispetto a un altro ben più massiccio, è soggetto alla sua forza di gravità e possiede una certa energia potenziale che è massima (ossia uguale a ZERO) quando il corpo è all’infinito, mentre decresce avvicinandosi al corpo centrale. L’energia potenziale è proprio un’energia “in potenza”. Ossia è capace di trasformarsi in movimento e diventare energia cinetica. In realtà l’energia potenziale è sempre negativa, dato che corrisponde a un lavoro che viene compiuto opponendosi alla forza e quindi il valore assoluto dell’energia potenziale cresce avvicinandosi al corpo centrale, ma l’energia è sempre più piccola. D’altra parte, più si è vicini e meno lavoro si deve compiere per opporsi alla gravità e raggiungere quel punto.
Come già detto, l’energia potenziale è sempre legata strettamente all’energia cinetica che dipende dalla velocità del corpo che subisce la forza di gravità. Se portiamo un oggetto a un’altezza h e poi lo lasciamo libero, esso ha acquistato una certa energia potenziale, che viene trasformata in energia cinetica mentre il corpo cade sempre più velocemente verso il corpo centrale.
La condizione fondamentale è che se il sistema (corpo centrale più oggetto orbitante) non cambia, l’energia totale dell’oggetto che subisce la forza di gravità deve rimanere costante. In altre parole, la somma di energia cinetica ed energia potenziale deve rimanere costante.
L’esempio più classico è sempre quello dell’ottovolante. Il carrello viene portato in alto in modo da aumentare la sua energia potenziale (diminuisce il suo valore assoluto). Poi viene lasciato libero ed acquista una velocità di caduta (ossia energia cinetica) a scapito dell’energia potenziale che diminuisce (aumenta il valore assoluto).
L’energia potenziale è come un “portafoglio” pieno di soldi. Finché stanno lì dentro sono una ricchezza “potenziale”. Appena si cominciano a spendere diventano qualcosa di pratico (energia cinetica) che rendono concreta la ricchezza. Purtroppo, però, il portafoglio è costretto a svuotarsi… Arrivati in fondo all’ottovolante abbiamo il portafoglio vuoto, ma tanti oggetti acquistati. Niente vieta, però, di rivendere gli oggetti acquistati e tornare in possesso dei soldi (ossia il carrello torna verso l’alto). Dobbiamo solo tenere presente che, nel mondo della meccanica classica (senza “attriti”, invidia, gelosia, egoismo, e cose del genere), vige una legge di un’onestà perfetta: ciò che si è comprato, si può rivendere allo stesso prezzo che si è pagato. Rivendendo tutto si ha di nuovo il portafoglio pieno (si è tornati col carrello all’altezza iniziale). Si sono persi gli oggetti comprati (si perde l’energia cinetica), ma si riempie di nuovo il portafoglio (energia potenziale).
La situazione cambia se un oggetto si pone in orbita circolare attorno al corpo centrale di massa M. In questo caso l’energia cinetica è dovuta alla velocità di rivoluzione del corpo in orbita. Le due energie devono, comunque, sempre essere legate tra loro. In tale caso, però, vi sono ben poche possibilità di azione. La situazione è molto più rigorosa. L’energia potenziale rimane COSTANTE dato che l’oggetto ruota attorno al corpo centrale sempre alla stessa distanza (il raggio R). Se non cambia l’energia potenziale, non può nemmeno cambiare l’energia cinetica (la loro somma deve restare costante) e l’oggetto si muove con una certa velocità di modulo costante che dipende dal raggio orbitale. Siamo in condizioni di equilibrio dinamico.
Scriviamo quanto detto con il linguaggio matematico:
Energia cinetica = EC = ½ m v2
Dove m è la massa dell’oggetto orbitante e v la velocità orbitale. Notiamo che questa energia SEMBRA scollegata totalmente dalla massa centrale M. Il fatto che non compaia M vuol dire che, in qualche modo, essa può “sopravvivere” inalterata anche se dovesse cambiare M. Teniamolo bene a mente…
Energia potenziale = EP = - GMm/R
Sappiamo già bene perché compare Il segno “meno”. R è la distanza a cui si trova l’oggetto orbitante, ossia il raggio orbitale.
L’energia totale orbitale, che deve conservarsi, è data dalla somma di queste due energie:
Etot = EC + EP = ½ m v2 - GMm/R
Queste semplici considerazioni potrebbero già darci una risposta molto provvisoria e “brutale”. Se cambio la massa M del Sole, cambia l’energia potenziale e potremmo dire che la velocità deve cambiare per mantenere l’energia totale. Arriveremmo a un assurdo, però. Alla stessa distanza R (nessuno ci impone di cambiarla) manterremmo un oggetto in orbita con una velocità maggiore. Le cose non possono andare così. L’errore commesso è stato quello di voler conservare l’energia totale! Essa deve conservarsi SOLO se non cambia il sistema, ma in questo caso il sistema è cambiato, dato che è cambiata la massa del Sole. In poche parole, cambiare la massa del Sole vuol dire cambiare l’energia del sistema. Anche questo è un punto da tener bene a mente.
Ritorniamo alla nostra energia totale con il Sole “normale” e riscriviamola:
Etot = ½ m v2 - GMm/R
Intanto, possiamo tranquillamente “eliminare” la massa m, dividendo tutto per m. Otteniamo un’energia per unità di massa che ci semplifica i calcoli senza cambiare sostanzialmente niente.
Etot = ½ v2 – GM/R
Siamo su un’orbita circolare e la Terra ha una sua velocità che può essere tranquillamente calcolata attraverso la terza legge di Keplero. Oltretutto essa è una velocità costante dato che l’orbita è circolare.
v2 = GM/R
Come vedete siamo riusciti a scrivere la velocità in funzione della massa M e del raggio dell’orbita.
L’energia cinetica (divisa per la massa m) diventa allora.
EC = GM/2R
Accidenti! E’ esattamente la metà dell’energia potenziale divisa per la massa m. Essa infatti vale proprio, in modulo, GM/R
Non meravigliatevi… abbiamo trovato che l’energia potenziale "regala" l’equilibrio al sistema, se l’energia cinetica è esattamente la sua metà. Non abbiamo fatto altro che scrivere il teorema del viriale (ricordate?). In ogni modo, torniamo alla nostra energia totale che può scriversi in modo estremamente semplificato:
Etot = GM/2R – GM/R = - GM/2R
L’energia totale orbitale non è altro che la metà dell’energia potenziale e dipende essenzialmente dal raggio R dell’orbita (M è sempre quella che è). In altre parole, l’energia orbitale è una costante per un certo raggio orbitale.
Cosa succederebbe se l’orbita fosse ellittica? Niente di veramente speciale… L’unico fatto importante sarebbe la variazione continua e periodica della distanza R. Ciò comporta un continuo cambiamento dell’energia potenziale e quindi di quella cinetica e, infine, della velocità. Per conservare l’energia orbitale, insomma, l’oggetto deve andare più veloce al perielio e più lento all’afelio. Tutto qui. Chi comanda è, comunque, sempre la conservazione dell’energia orbitale.
In conclusione, si trova che l’energia orbitale è una funzione del solo semiasse dell’orbita. Ne segue che l’energia orbitale di un’orbita circolare di raggio R è la stessa di un’orbita ellittica di semiasse a = R. In altre parole, l’energia non dipende assolutamente dall’eccentricità orbitale. L’unica differenza è che mentre nell’orbita circolare le due energie si mantengono sempre uguali, in quella ellittica continuano a cambiare, mantenendo, però, sempre uguale la loro somma.
A questo punto abbiamo in mano tutte le informazioni per studiare ciò che capita se il Sole perdesse parte della sua massa. Torniamo a un’orbita circolare e alla nostra Terra. Abbiamo già visto come è semplice il caso in cui il Sole sparisse del tutto: la Terra proseguirebbe di moto rettilineo uniforme con una velocità che è uguale in modulo alla velocità orbitale che aveva quanto girava attorno al Sole. Una prova in più che la velocità orbitale è in qualche modo indipendente dalla presenza del Sole. Esso non fa altro che obbligarla a cambiare continuamente direzione, ma non può cambiargli il modulo.
D’altra parte, basta prendere la formula dell’energia e azzerare M. Otteniamo:
Etot = ½ v2 – GM/R = ½ v2 – 0 = ½ v2
L’energia è solo cinetica e rimane esattamente quella del moto circolare. La direzione è costante e la Terra se ne va “per la tangente” con velocità v. Ovviamente, l’energia totale non si è conservata dato che è cambiato il sistema, avendo annullato il Sole, la sua forza di gravità e l’energia potenziale.
Passiamo a casi meno drastici e più generali.
Scriviamo nuovamente l’energia dell’orbita originaria, tenendo conto del legame tra energia cinetica ed energia potenziale. Si ha:
Etot,O = GMO/2aO – GMO/aO = - GMO/2aO
Abbiamo solo inserito il semiasse aO di una ipotetica orbita ellittica, che nel nostro caso vale proprio R, sapendo che l’energia non cambierebbe.
Iniziamo a diminuire la massa solare…
Ciò che capita immediatamente è che cambia l’energia potenziale. L’energia cinetica, invece, resta quella che è. Possiamo scrivere:
Etot,N = EC,O – EP,N = GMO/2aO – GMN/aO …. (1)
Notate che abbiamo indicato con indice “N” le quantità moficate (Nuove) e con indice O quelle originali.
Tuttavia, in questa nuova situazione, abbiamo che l’energia potenziale è diminuita in valore assoluto ed è, quindi, aumentata come valore negativo. L’energia cinetica è rimasta uguale e quindi l’energia totale è aumentata solo in base all’energia potenziale. Ne segue che l’orbita deve allargarsi. Ma se l’orbita si allarga, la velocità deve scendere. Oltretutto allargandosi l’orbita, aumenta ancora l’energia potenziale. La configurazione finale, stabile, deve portare (come ormai sappiamo molto bene) a un valore dell’energia cinetica pari alla metà dell’energia potenziale, ossia:
Etot,N = - GMN/2aN …. (2)
L’energia (1) diventa (2), ma deve rimanere sempre uguale, dato che in entrambi i casi stiamo usando la nuova massa solare, ossia uno stesso sistema. Siamo di fronte a un processo di assestamento orbitale.
Uguagliando le due relazioni si ottiene:
GMO/2aO – GMN/aO = - GMN/2aN
Moltiplicando entrambi i membri per 2aN/GMO, otteniamo:
2GMOaN/(2aO GMO) – 2GMNaN/(aOGMO) = - (GMN/2aN) (2aN/GMO)
aN/aO – 2aNMN/MOaO = - MN/MO
e ancora:
aN/aO (1 – 2MN/MO) = - MN/MO
aN/aO = - (MN/MO)/(1 – 2MN/MO)
aN/aO = (MN/MO)/(2MN/MO – 1) …. (3)
Questa formula permette di calcolare il nuovo semiasse in funzione della variazione di massa solare.
Studiamo rapidamente questa funzione, ponendo y = aN/aO e x = MN/M0.
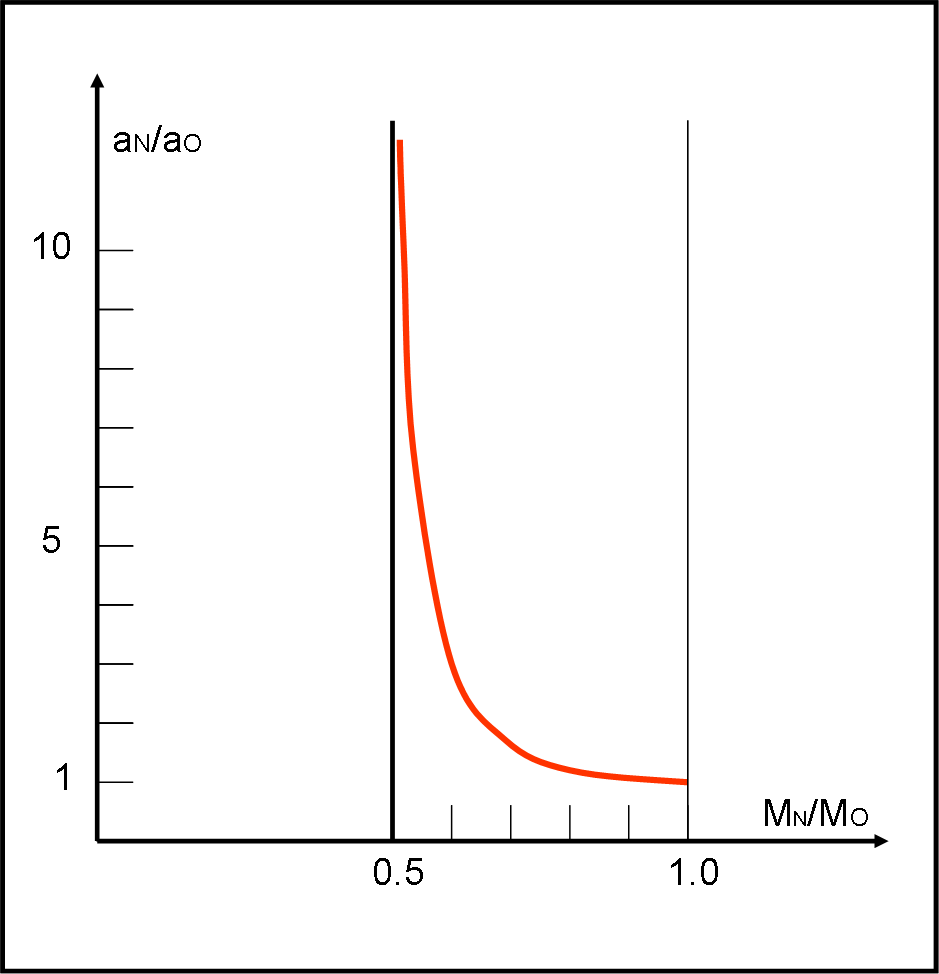
y = x/(2x – 1)
Se il Sole diminuisce la propria massa, il valore di x è compreso (teoricamente) tra 1 e 0. Tuttavia, stiamo molto attenti al valore x = ½. Per quel valore il denominatore della funzione va a zero e la y va a infinito. Possiamo quindi solo permetterci una perdita di massa minore di 0.5 se no… addio caro Sole! Notiamo anche (potete provarlo facilmente) che per x vicino a 1 la variazione del’asse è molto contenuta, ma se si avvicina a 0.5 il semiasse aumenta in modo rapidissimo. Non esistono massimi o minimi dato che la derivata prima non si annulla mai (provate…).
Ne consegue che poco interessa scendere a valori di x minori di 0.5 dato che per quel valore il semiasse va a infinito e quindi la Terra abbandona il Sole su una traiettoria parabolica, come già abbiamo determinato precedentemente. In realtà, avremmo orbite iperboliche fino a raggiungere una situazione degenere (retta) per x = 0. Tuttavia, è inutile esagerare con calcoli puramente accademici…
La funzione è rappresentata nella figura che segue.