Categorie: Astronomia Elementare Quiz
Tags: declinazione Eratostene latitudine Nobody ombra pappidi quiz Sole
Scritto da: Vincenzo Zappalà
Commenti:17
QUIZ: seguendo Eratostene… **
Un problemino di astronomia classica che Eratostene avrebbe risolto in un battibaleno. Altrettanto, penso, riuscirebbe a fare il nostro Pautasso, celebre conoscitore dei moti solari oltre che di marroni cuneesi. Entrambi, perciò, si tengano ben lontani da darne la soluzione…
Nobody porta nel sonno i tre pappidi (Peppa, Pippo e Pappo) in un luogo dell’emisfero nord (quando dormono, non li svegliano nemmeno le cannonate). Hanno con loro solo una bella asta solida ma leggera (chiamarla gnomone sarebbe riduttivo…) di ben 1000 metri di lunghezza e un metro per misurare le distanza (estremamente lungo…). Se vogliono tornare a casa devono determinare la latitudine del luogo e la declinazione del Sole nel giorno in cui hanno deciso di fare il loro tentativo di determinazione.
I tre ragazzi non si scoraggiano e piantano l’asta per bene al suolo, in perfetta posizione verticale. Aspettano il primo giorno favorevole (che sia soprattutto sereno) e decidono di fare due misurazioni nello stesso giorno: una nel momento in cui l’ombra proiettata dall’asta è la più corta e una nel momento in cui è la più lunga.
Nel primo caso ottengono un valore di 1732 metri, nel secondo caso di 5671 meri. I tre piccoli geni fanno pochi calcoli e mandano il risultato a Nobody, che è costretto a liberarli…
Ovviamente, consideriamo la Terra sferica, il Sole puntiforme e all'infinito, e nulla la rifrazione atmosferica.
Ribadisco che il Sig. Pautasso e i suoi amici si facciano sentire solo in via privata, così come farà Eratostene (con lui ci sentiamo spesso…).
QUI la soluzione





17 commenti
Pautasso ha detto "obbedisco" ed è uscito con Arley a cercare tartufi.
Eratostene si trova in una zona dove non c'e segnale, quindi non può intervenire.
meno male... e occhio ai serpenti corallo (sono buoni, ma se vogliono non perdonano... controlla bene i colori, magari sono quelli innocui... la Sardegna ne sa una più del diavolo!!!!) che solitamente si nascondono sotto i marroni...
temo che in questo circolo astronomico, l'astronomia non piaccia tanto...
Va bene... Mau-Pau puoi incominciare a dare il risultato finale, senza spiegare i passaggi e vediamo se qualcuno si muove. Meno male che Eratostene è in viaggio , altrimenti si sarebbe offeso... dopo più di duemila anni ha insegnato ben poco...
Lo levo dall'evidenza...
Caro Enzo, preferisco dare, per ora, un primo risultato parziale.
La somma della colatitudine del luogo e della declinazione del sole nel momento della misura più piccola, pari a 1732 metri, fornisce un angolo di 30°.
Ricordo che la colatitudine = 90° - latitudine.
Vediamo se qualcuno può giustificare questo primo risultato.
Piace, piace! ma non significa poi sapere risolvere i quiz.
Per quanto mi riguarda, forse sono arrivato al valore della latitudine-declinazione utilizzando il valore di 1732m dell'ombra più corta, L-δ≈60° (?)
Dell'altro valore, prima ancora di capire come utilizzarlo, sto ancora cercando di capirne il significato.
io stavo scherzando, ragazzi! So benissimo che siete sempre pronti a provare... ma voglio essere sincero:
C'è un piccolo inghippo nel problema... che potrebbe creare qualche difficoltà. Basta riflettere per bene e leggere cosa dice l'enunciato... la lampadina dovrebbe accendersi...
Una bella figura dovrebbe risolvere la faccenda...
Le ombre sono molto lunghe in due momenti della giornata: l'alba e il tramonto che sono momenti simmetrici rispetto il mezzogiorno e la mezzanotte.
La pronunciata lunghezza delle ombre in questi due momenti dipende dal fatto che i raggi del sole sono radenti, paralleli al piano locale, dato che il sole sta risalendo sopra la linea dell'orizzonte (alba) o sta scendendone al di sotto (tramonto).
Raggi paralleli al suolo generano ombre di lunghezza infinita che non siamo in grado di misurare.
Procedendo verso il polo Nord (nell'emisfero settentrionale), alle latitudini superiori ad un certo valore, che si trova facilmente, al solstizio estivo non ci sono più tramonti perché il sole non scende sotto la linea dell'orizzonte, ma semplicemente vi si avvicina ed i suoi raggi hanno una inclinazione superiore a zero, tale da proiettare un'ombra di lunghezza finita e misurabile.
Naturalmente, subito dopo questo minimo, la altezza del sole inizia a crescere ( potremmo dire che questa specie di alba segue immediatamente il "tramonto" inteso come discesa alla minima altezza.
Conoscendo la misura della lunghezza dell'ombra nel momento di minima altezza del sole e l'altezza dello stilo...
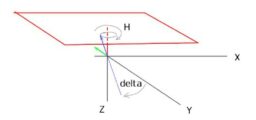
Un prima figura preliminare può essere questa...
Si tratta poi di mettere in relazione per le due situazioni i valori di declinazione e latitudine.
Due relazioni, due incognite...
Come la vecchia pubblicità del 1984 (due gusti, due baci) https://www.youtube.com/watch?v=KvOZGJcs2vk
È la meta della semplice differenza di due angoli 60 e 80 gradi , cioè 10 gradi di colatitudine. Cioè 80 gradi latitudine nord . Siamo ovviamente oltre il circolo polare artico perché altrimenti l ombra del tramonto sarebbe di lunghezza infinita
e la declinazione del Sole? e un minimo di calcoli... sei sempre ultra-conciso Leandro...
Non ho a disposizione un pc purtroppo. Direi comunque che deve esserci il sole sia all alba che al tramonto . Sicuramente tra i due equinozi , con il sole alto circa 20 gradi, minuto piu minuto meno.
sei ultra-perdonato! Appena puoi fai il calcoletto...
da semplici considerazioni geometriche
delta + beta + 90+alfa =180
delta + gamma + 90- alfa = 180
da cui
delta +beta +alfa = 90
delta + gamma -alfa = 90
stante che
Ombra corta = 1 x tg beta
Ombra lunga = 1 x tg gamma
si calcola
beta = 60
gamma= 80
quindi il sistema di due eq in 2 incognite diviene
delta + alfa = 30
delta - alfa = 10
da cui
delta = 20
alfa = 10
delta è la declinazine dei raggi solari
alfa è la colatitudine del luogo = 90-latitudine .
La misurazione dovrebbe essere stata efettuata circa il giorno 22 luglio.
Benché la data della misurazione non fosse richiesta da Nobody, possiamo fare qualche interessante ragionamento su questa informazione.
Se supponiamo che i Pappidi la conoscano ( il che è ragionevole), questa informazione potrebbe essere usata in alternativa alla esecuzione della seconda misura, sapendo come varia la declinazione del Sole nel corso dell'anno, una relazione non difficile da trovare in via approssimata.
Ci troveremmo in una situazione in cui il lettore non può dare una risposta ma è certo che i protagonisti del quiz la possono dare.
Comunque, tornando alla soluzione data da Leandro, oltre al 22 luglio (dopo il solstizio estivo) , un'altra data in cui la declinazione del Sole è di 20° è il 20 maggio ( prima del solstizio), ma non vedo indizi che ci permettano di dire quale delle due date sia proprio quella della misurazione, a meno che non ipotizziamo che la prova si sia svolta quest'anno, nel qual caso la data precisa è il 20 maggio, dato che luglio deve ancora arrivare.
Insomma, sapendo la data della misurazione potremmo dire univocamente il valore della declinazione del Sole in quel giorno, mentre conoscendo il valore della declinazione non si risale univocamente alla data.
Questo quiz mi ha ricordato il titolo di un bel libro letto qualche anno fa. Il libro, che raccontava la vita di una famiglia Inuit, s'intitolava "Paese dalle ombre lunghe". Un titolo che rimane suggestivo, ma non totalmente corretto. Da questo quiz ho capito che a quelle latitudini le ombre non sempre sono poi così lunghe rispetto alle nostre verso il tramonto.
Considerando che:
l = lunghezza dello gnomone = 1000 m.
L1 = lunghezza minima dell’ombra dello gnomone = 1732 m.
L2 = lunghezza massima dell’ombra dello gnomone = 5671 m.
Alt.max (del Sole) = arctan (l / L1) = arctan(1000 / 1732) ≈ 30°
Alt.min (del Sole) = arctan (l / L2) = arctan(1000 / 5671) ≈ 10°
Prendendo come riferimento l'ottimo disegno di Leandro e le prime due righe di considerazioni geometriche:
δ + β + 90 + α =180
δ + γ + 90 - α = 180
e sommando le due espressioni:
2δ + β + γ + 180 = 360
δ = (180 – β – γ) / 2 (1)
ma
β = 90 – Alt.max (angoli complementari di un triangolo rettangolo)
γ = 90 – Alt.min (angoli complementari di un triangolo rettangolo)
la (1) si può scrivere:
δ = (180 – 90 + Alt.max – 90 + Alt.min) / 2
δ = (Alt.max + Alt.min) / 2
che dovrebbe essere la formula generale;
invece, per il calcolo della latitudine
δ + β + 90 + α =180 => δ + 90 – Alt.max + 90 + α =180 =>
δ + 90 – Alt.max = 90 - α ma 90 – α = latitudine =>
latitudine = 90 – Alt.max + δ = 90 – 30 + 20 = 80°
Per quanto riguarda la data, come ha scritto Maurizio, sono 2 quelle dove la declinazione è uguale o molto prossima a 20°, equidistanti dal solstizio d’estate:
solstizio d’estate 21 giugno = 172 giorno dell’anno (non bisestile)
23 luglio = giorno 204
20 maggio = giorno 140
| 172 – 204 | = 32 | 172 – 140 | = 32
qui un’animazione carina: http://astro.unl.edu/naap/motion3/animations/sunmotions.html