Questo articolo è inserito nella sezione d'archivio "Spaziotempo/Cosmologia"

Abbiamo introdotto il discorso in modo leggero e - speriamo - divertente con due raccontini di fantascienza, ma l'obiettivo era estremanente serio e didattico: parlare - anzi parlare di nuovo - di distanze tra galassie, di espansione dell'Universo, di cosa vediamo quando osserviamo il cosmo e di come calcolare la durata del viaggio della luce che ci raggiunge. Insomma l'ABC per chi desidera muovere i primi passi nel teatro dell'astronomia!

Per chi se li è persi, questi i racconti scritti da Mauritius che, scherzando, si ispirano a fenomeni che non sono così fantasiosi come possono sembrare a prima vista.

TOPOGRAFIA COSMICA: L'antefatto

TOPOGRAFIA COSMICA: Il problema da risolvere

Nell'articolo che segue (il primo della nuova generazione di quiz che abbiamo annunciato QUI) richiameremo concetti relativi all'espansione dell'Universo già spiegati in passato e andremo anche un pochino oltre, arrivando a sfiorare la metrica di Lemaitre e dei suoi collaboratori.

Un utile ripasso per molti, un occasione di approfondimento per altri, un po' di sano divertimento (speriamo!) per tutti!

PARTE PRIMA

Più veloci della luce **

(a cura di Maurizio Bernardi)

Queste le domande a cui, se vi fa piacere (a noi ne fareste molto!), potete provare a rispondere (nei commenti) prima di continuare a leggere:

1. Possono due galassie allontanarsi tra loro più velocemente della luce?
2. Se esistesse una galassia che si allontana da noi alla velocità della luce, la potremmo ancora vedere?
3. Sarebbe all'interno del nostro Universo osservabile?
4. A che distanza si troverebbe?

E se le risposte non le conoscete (o pensate di conoscerle, ma avete dei dubbi), vi consigliamo di leggere questo articolo per le prime tre:

COSA, COME E QUANDO SI OSSERVA NELL'UNIVERSO

e questo per la quarta:

LA SFERA DI HUBBLE E TUTTO CIO' CHE NON VEDREMO MAI

**********************************************************

Poco più di un secolo fa, nel 1915, un fisico tedesco di nome Alfred Wegener formulò l'ipotesi che, attorno a 300 milioni di anni fa, tutti i continenti fossero uniti in un unico territorio detto, dal greco, Pangea. Una cosa simile...

Ma con quale meccanismo si fossero poi separati i vari pezzi non seppe spiegarlo. Una cinquantina di anni più tardi la spiegazione si trovò nella teoria delle placche tettoniche: la differenza di temperatura tra interno ed esterno della terra genera moti convettivi che creano le “crepe” destinate ad allargarsi sempre più. Oggi sappiamo che il Sudamerica e l'Africa si stanno allontanando alla velocità di 2 cm all'anno. Non molto, direte, ma intanto i due continenti sono separati da cinquemila chilometri e se oggi il movimento è di una lentezza esasperante, in passato sarà certo stato molto più rapido. (E c'è anche qualcuno che sospetta che una mano l'abbiano data pure gli amici asteroidi).

Questo per dire che anche se uno se ne sta fermo, qualcosa si muove, eppur... si muove!

Solo quattordici anni dopo l'ipotesi di Wegener, nel 1929, Edwin Hubble annunciò che quasi tutte le galassie stavano allontanandosi da noi. Ma questo fatto non si limita a “noi”, la nostra galassia, è proprio la regola generale, per cui tutti si stanno allontanando da tutti gli altri: l'Universo si sta espandendo.

Per capire quanto veloce sia questo allontanamento reciproco ricorriamo all'analisi dei segnali che riceviamo dalle altre galassie. La loro luce si sposta verso lunghezze d'onda maggiori in funzione del tempo impiegato nel lungo viaggio dall'invio fino alla ricezione. Questo spostamento sempre più grande per tempi sempre più lunghi, rappresenta il redshift, effetto che ricorda solo apparentemente l'effetto doppler, in quanto non è dovuto a un effettivo allontanamento di oggetti nello spazio, ma allo stesso spazio che si dilata.

Questo implica che la velocità di recessione aumenti con l'aumentare della distanza. Il nuovo spazio che si genera va crescendo con la distanza come capiterebbe per tanti  punti disegnati su un palloncino che si gonfi.

Se la deriva dei continenti si accontenta di una velocità di 2 cm all'anno, la recessione delle galassie è un fenomeno molto, ma molto più rapido. Quanto rapido?

La velocità di recessione segue in prima approssimazione una legge lineare e la possiamo esprimere con questa semplice formula:

v = H₀ d     ....(1)

dove v è la velocità di allontanamento, d è la distanza attuale dalla galassia (sì ma fate presto a fare i conti perché nel frattempo si muove), e H₀ ?

Se aveste letto questo interessante articolo, sapreste che H₀ è la “costante” di Hubble.

Ecco, ve ne cito solo un breve ma significativo frammento…

“H è una costante per un certo istante t. Ossia, vale per tutto l’Universo, ma solo in un ben definito istante. Cambiando il tempo, cambia anche la costante. La sua variazione dipende soprattutto dal tasso di espansione e dalla variazione della sua velocità.

Da quanto detto, non è difficile ricavare il raggio r della sfera di Hubble OGGI, che è definita come il luogo dei punti (spaziali) in cui la velocità di allontanamento delle galassie (e di qualsiasi altra cosa) vale proprio c, ossia la velocità della luce. Può quindi essere scritto semplicemente come:

r = c/H

Per chi si ricorda come si può determinare l’età dell’Universo, questa formula non è nuova. Proprio l’inverso di H è il tempo di esistenza del Cosmo.

Infatti, sappiamo che una velocità è uguale a uno spazio diviso per un tempo, ossia v = s/t.

Ammettendo che l’espansione sia sempre stata costante, possiamo considerare la distanza s uguale alla distanza d del Big Bang. Dalla (1), ovvero v = H₀ d, segue che:

v = s/t = dBB/tBB = H dBB

ossia:

tBB = 1/H

Ne segue che, teoricamente, il raggio della sfera di Hubble dovrebbe essere proprio la distanza percorsa dalla luce durante la vita dell’Universo: 13.7 miliardi di anni (tempo!), ossia 13.7 miliardi di anni luce (distanza!). In realtà, questo raggio è leggermente più lungo a causa della non regolarità di variazione della costante di Hubble durante le varie fasi evolutive e si pensa si aggiri intorno ai 14-15 miliardi di anni luce. “

Notevole, vero ?

Il valore attribuito oggi alla costante di Hubble è  67 Km/s/Mpc. In altre parole per ogni Mpc (Megaparsec = 3,26 * 10⁶ anni luce) di distanza, la velocità cresce di 67 Km/s.

Se una galassia che si trova a tre milioni di anni luce da noi, scappa via a 67 Km/s, quale sarà la velocità di recessione di una galassia che osserviamo a 300 milioni di anni luce da noi? Ben 6.700 km/s !

In realtà ci sono alcune eccezioni "apparenti"... La galassia M31, per gli amici Andromeda, non si allontana affatto da noi e, pur trovandosi a due milioni e mezzo di anni luce, si sta avvicinando alla velocità di 300 Km/s. Si mormora che tra 2,5 miliardi di anni ci piomberà addosso, assieme alle sue 14 galassie nane satelliti, fondendosi con noi. Non ci resta che aspettare per vedere se è vero. Non è certo una stranezza solo della nostra vicina di casa, ma di qualsiasi galassia che è dotata di un suo moto proprio nello spazio, legato soprattutto alla gravità esistente all'interno del gruppo locale a cui appartiene. Un vero movimento spaziale che può essere trascurato per distanze relative veramente grandi, per le quali la velocità di recessione dovuta allo spazio che si dilata diventa dominante.

Ma se una galassiasi trova proprio lontano lontano? Ad esempio, ad una distanza tale che la velocità di recessione superi addirittura la velocità della luce (ma sarà mai possibile)?

Ebbene, lo spazio si espande velocemente, ma non c'è nulla nello spazio nascente a cui attribuire un vero movimento. Le due galassie possono essere considerate immobili e la velocità, che è uno spostamento di "qualcosa" nell'unità di tempo, assume un significato del tutto diverso. La chiamiamo comunque velocità di recessione, ma è legata solo al tasso di espansione.

Nondimeno, le posizioni relative di due galassie molto lontane tra loro mutano continuamente e, se misuriamo le loro distanze in tempi diversi, rapportando la differenza di distanza al tempo trascorso, troviamo un valore che può essere superiore a quello di c (c = velocità della luce nel vuoto)

Ma su questa scala di distanze varrà ancora la legge di linearità che abbiamo applicato?

E la costante di Hubble da considerare, sarà quella del nostro “oggi”?

Intanto vediamo di dare qualche risposta alle domande del quiz...

Possono due galassie allontanarsi tra loro più velocemente della luce?

Da quanto abbiamo detto sopra la cosa è possibile: due galassie possono allontanarsi a velocità superiore a quella della luce non per un loro moto proprio, ma per effetto della generazione di nuovo spazio tra di loro, a causa dell'espansione dell'Universo. La velocità della luce, infatti, è un limite invalicabile solo per corpi che appartengono allo spazio, non è assolutamente un limite per lo spazio! 

Se esistesse una galassia che si allontana da noi alla velocità della luce, la potremmo ancora vedere?

Per dare una risposta occorre ragionare sul percorso della luce deformato dall'espansione dell'universo, nel corso del tempo. Certo possiamo vedere la galassia lontana non come è, ma come era, così come possiamo vedere oggi un vecchio film in cui il giovane attore protagonista non è più tra noi da decenni, essendo defunto in tarda età.

Quella che riusciamo a vedere è una sorta di luce “in scatola” confezionata e spedita attraverso la curva adagiata su di un cono di luce che collega il passato della galassia al nostro presente, ossia il percorso realmente effettuato dalla scatola-luce tra il suo invio e la consegna del "postino" (vedi fig. 2)

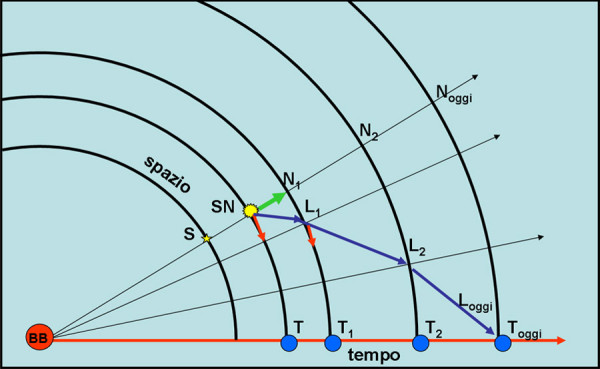
Anche questi concetti sono esposti in modo ben più efficace e dettagliato in uno degli articoli che potete trovare in archivio, più precisamente, questo.

Ne riportiamo un significativo passaggio.

“Per distanze veramente grandi, maggiori di un paio di miliardi di anni luce, lo spazio non può approssimarsi come immobile, o meglio statico. Esso si espande continuamente e il percorso della luce compiuto in un certo periodo di tempo è ben maggiore di quello relativo alla differenza di tempo tra quando i fotoni sono stati emessi e OGGI. In altre parole, dire che una galassia è vecchia di 10 miliardi di anni è ancora esatto, ma dire che essa dista 10 miliardi anni luce da noi NON è per niente esatto. “

La terza domanda chiedeva: Possiamo dire che la galassia che si allontana da noi alla velocità della luce si trova all'interno del nostro universo osservabile?

Innanzitutto definiamo l'Universo Osservabile come l’insieme degli oggetti, nella distribuzione spaziale odierna, di tutto ciò che siamo in grado di vedere nel cono di luce odierno.

Nella figura che segue, il cono di luce odierno (l'insieme di tutti gli oggetti che vediamo oggi, tra cui la supernova SN) è la curva azzurra a forma di goccia, mentre l'Universo Osservabile è l'arco di circonferenza azzurro, di cui fanno parte anche la Terra T e l'ormai ex-supernova SN, diventata un buco nero.

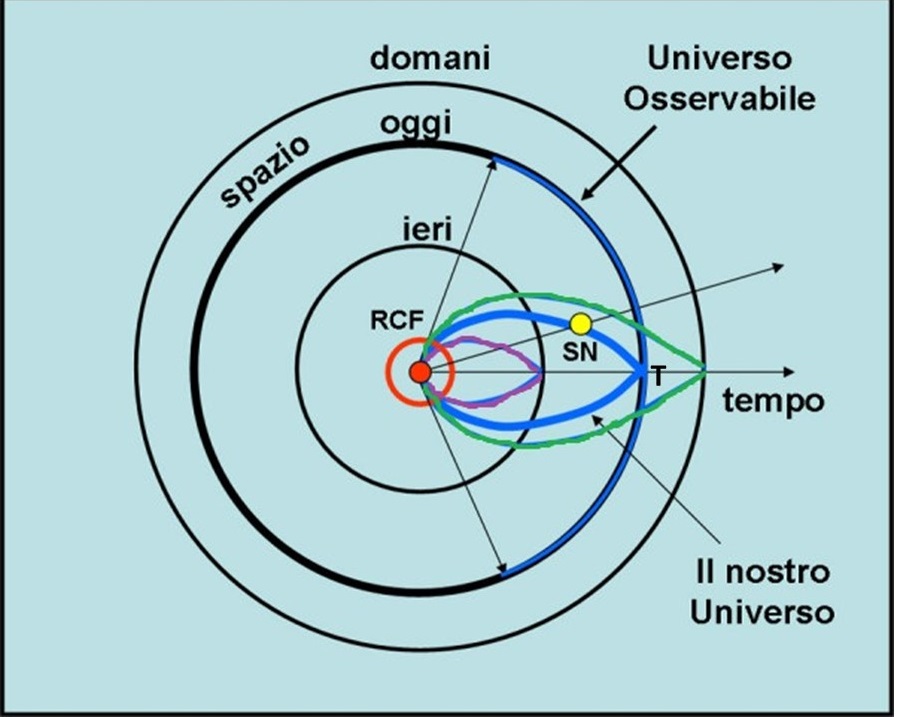
Quindi la risposta alla domanda è SI: se la luce della galassia ci ha raggiunti e la vediamo com'era un tot di anni fa, essa continuerà sempre a fare parte del nostro Universo Osservabile, qualunque sia la velocità con cui si allontana da noi.

N.B. quando sentiamo dire che una galassia è a tre miliardi di anni luce da noi, significa che la sua luce ha impiegato tre miliardi di anni per raggiungerci, ma NON significa che la sua distanza attuale da noi ammonta a tre miliardi di anni luce: oggi quella galassia si trova (nel nostro Universo Osservabile) ad una distanza maggiore, a causa dell'espansione subita dall'Universo dal momento in cui è partita la luce che vediamo, ad oggi.

Veniamo alla quarta  domanda: A che distanza si troverebbe ?

Se consideriamo la relazione v = H₀ / d , essendo noto il valore H₀ (attuale) e il fatto che v=c

possiamo valutare la distanza d= c/H₀ e sostituendo i valori noti, ottenere:

d = 300.000 km/s / 67 km/s /Mpc = 4477 Megaparsec

oppure 4477*3,2*10^6 = 14,3 miliardi di anni luce

Tutto chiaro?

Se sì, siete pronti per tuffarvi nell'approfondimento che segue, se no... chiedete, chiedete, chiedete!

E non dimenticate che gli argomenti qui esposti in modo estremamente sintetico, li trovate spiegati con dovizia di particolari QUI e QUI.

PARTE SECONDA

Veloci come la luce ***

(a cura di Vincenzo Zappalà)

Abbiamo solo uno strumento per capire quanto tempo ha viaggiato la luce che riceviamo da una galassia lontana lontana: il REDSHIFT COSMOLOGICO. Non basta affidarsi alla costante di Hubble, che è costante ovunque ma non per sempre. L'espansione dello spazio si è verificata con valori di H progressivamente più piccoli. Oggi sappiamo che H vale circa 67 Km/s/Mpc ma quanto valeva al momento il cui la galassia lontana lontana ha inviato la sua luce? E come si è modificato questo valore durante il viaggio compiuto dai fotoni? Ma, soprattutto, cosa rappresenta veramente  la costante di Hubble?

Mentre riflettiamo su tutto ciò, possiamo affrontare la quinta domanda: Che valore ha il redshift  di una  galassia lontana lontana che si allontana da noi alla velocità della luce?

Ci può aiutare, nell'impostazione del nostro ragionamento, una figura di questo genere, che riportiamo parzialmente  da un articolo di qualche anno fa, in cui  è stata proposta come quadro riassuntivo di tutto lo scenario.

Qualcuno se la ricorda? Sa come completarla e servirsene per rispondere alla domanda?

N.B.: La soluzione tramite la figura è di tipo occhiometrico, ovvero basata sulla comprensione concettuale della relazione tra cono di luce e redshift. Ne esiste anche un'altra più precisa, di tipo matematico, che necessita la conoscenza della metrica ricavata dalle equazioni di Einstein. La seconda non fa per noi (o, almeno, supera di molto i limiti divulgativi del nostro Circolo). Nella risposta si cercherà di mediare tra le due...

Se pensate di poter rispondere, potete farlo nei commenti, altrimenti proseguite nella lettura.

Eventualmente, prima di tentare la soluzione, potete leggere QUESTO ARTICOLO , ma fate bene attenzione... per legare il redshift cosmologico alla distanza attuale serve qualcosa di più che la legge di Hubble, di cui abbiamo parlato nella prima parte dell'articolo, e/o l'effetto doppler relativistico. Servono le equazioni di Einstein... ma è possibile aggirarle con la migliore approssimazione possibile.

*****************************************************************

La soluzione che stiamo per dare sarà, in parte, per via grafica, accettando uno dei modelli cosmologici tra i più utilizzati (con tanto di accelerazione dell'espansione). Non una semplice soluzione, perciò, ma una visione dell'Universo un po' diversa dal solito. Spero che permetta di comprendere ancora meglio certi concetti base dell'evoluzione del Cosmo, già trattati ripetute volte nelle pagine di questo Circolo.

La legge di Hubble  (v_r = H d) è sicuramente una legge fondamentale, ma il suo valore si limita a legare tra loro la velocità di recessione (v_r, dovuta allo spazio che si espande) e la distanza d a un certo tempo t. Riesce a farlo attraverso la costante di Hubble (H), che è costante solo per quanto riguarda il tempo t, ossia è la stessa in ogni punto dell’Universo, ma varia al variare del tempo.

Anche accettando un’espansione lineare dello spazio rispetto al tempo, la costante di Hubble varia in continuazione, dato che, ammettendo una relazione lineare, la derivata prima  (ossia la velocità) è costante rispetto al tempo, ma H è data dal rapporto tra velocità e distanza e la distanza continua a crescere nel tempo, causando una diminuzione del valore di H. Questa visione  non è mai abbastanza pubblicizzata, ma vedremo la sua utilità nel seguito dell’articolo.

Ma il problema vero, per gli oggetti molto lontani, è che l’unica cosa che si riesce a osservare è il redshift z e qui le cose si complicano, perché il legame tra la velocità di recessione e il redshift necessita delle equazioni della Relatività Generale e della scelta del modello evolutivo. In altre parole, la velocità di recessione, necessaria per stabilire una distanza OGGI può essere ricavata solo attraverso il REDSHIFT. Quest’ultimo però ci indica la variazione di una lunghezza d’onda nell’intervallo di tempo che va dall’emissione della luce fino al suo ricevimento e quindi deve  essere forzatamente legato al modello di espansione: la luce viaggia per più o meno tempo solo in funzione del tasso di espansione.

Non basta certo pensare di applicare la Relatività Ristretta per velocità prossime a quella della luce, dato che lo spazio in espansione (come abbiamo spiegato nella prima parte di questo articolo) può generare velocità di recessione anche maggiori (senza andare contro le ipotesi einsteniane). Questo è il punto chiave per comprendere l’enorme differenza concettuale tra effetto doppler e redshift cosmologico. Il primo corrisponde a un effettivo moto tra due oggetti nello Spazio e quindi la velocità della luce non può esser superata (in accordo con la RR), il secondo corrisponde a due oggetti immobili, che si allontanano solo per effetto dell’espansione dello spazio che li contiene (il famoso palloncino che si gonfia o il panettone con l’uvetta che lievita).

Né tanto meno potremmo usare la relazione lineare v = cz, classica dell’effetto doppler per piccole velocità. La Fig. 1 mostra le due ipotesi semplificate e quella calcolata attraverso il modello assoggettato alla RG e a particolari parametri (densità critica).

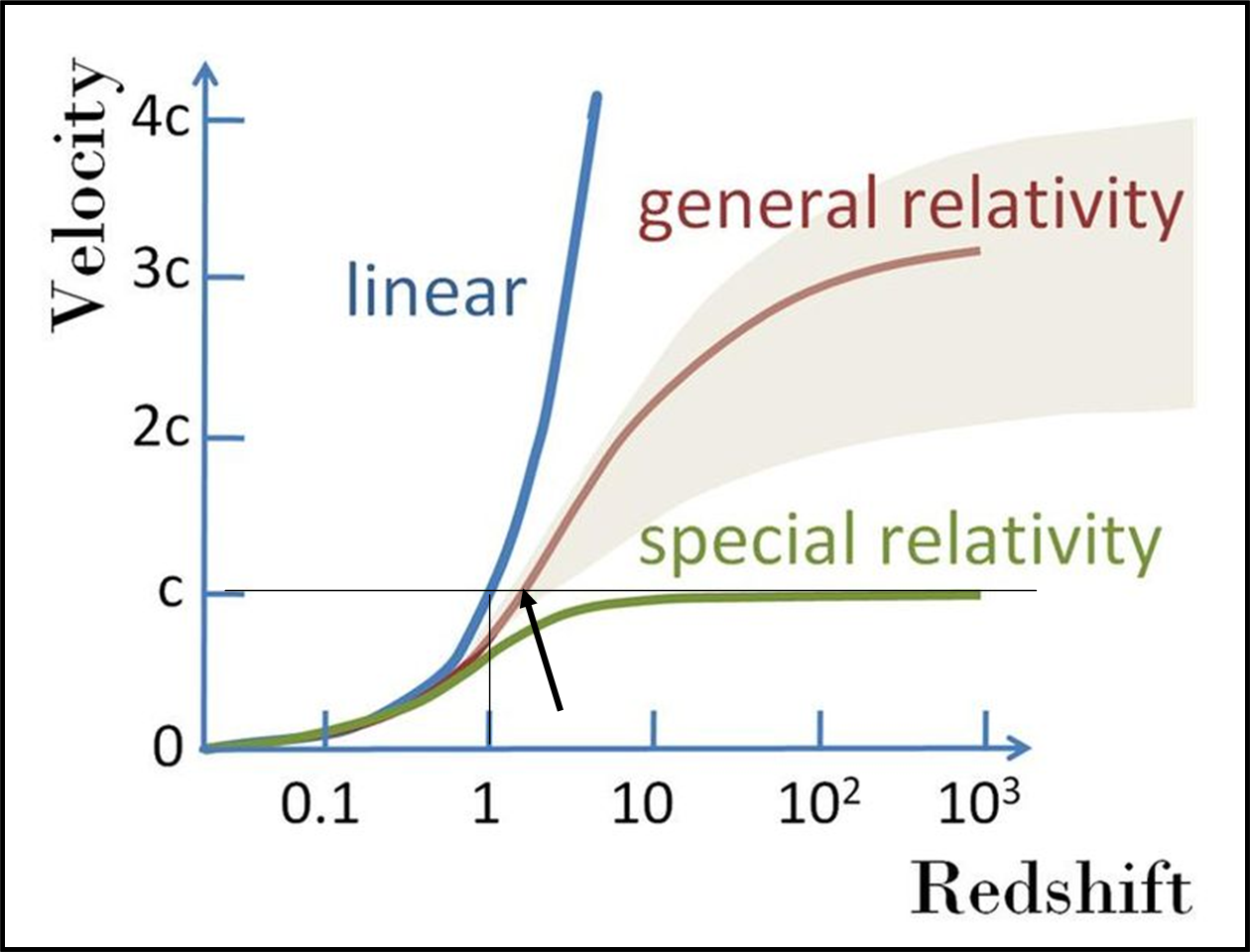
Dato che H è funzione del tempo e del modello scelto possiamo immaginare sia un aumento che una diminuzione della distanza di Hubble, per cui alcune galassie che sembrano ormai fuori dalla nostra possibilità osservativa potrebbero rientrarci, ma anche il viceversa. Per un Universo accelerato (come pensano oggi) la distanza di Hubble diminuisce ed è più facile scappare per sempre.

Dedichiamoci, perciò, al redshift cosmologico e vediamo come manovrarlo per i nostri scopi. Lui è l’unica “cosa” che riusciamo a osservare. Tutto il resta deriva dai parametri che si usano per l’espansione.

Il redshift parla solo con le lunghezze d’onda..

z = (λo – λe)/λe = λo/λe – 1                           …. (1)

dove λo è la lunghezza d’onda osservata oggi e λe è quella relativa al momento dell’emissione. Dentro al redshift vi è perciò tutto il viaggio che ha dovuto compiere la luce in un ambiente (spazio) che si stava espandendo.

E’ interessante richiamare un visione “alternativa” del redshift basato non sulla lunghezza da percorrere in uno spazio in continua espansione, ma a un tempo che subisce una dilatazione.  Una rappresentazione temporale e non spaziale dell’espansione dell’Universo. Essa non sarebbe altro che una dilatazione del tempo. Infatti, se aumentiamo la lunghezza d’onda, un orologio che segni il tempo in base a due creste successive, rallenterà sempre di più: il suo tic –tac diventerà tic ----- tac.

Ripetiamo: non sarebbe lo spazio che aumenta, ma l’orologio della luce (ossia la lunghezza d’onda) che rallenta. In realtà vi sono ancora dibattiti e polemiche accese a questo riguardo… Vale la pena fermarsi a pensare  a riflettere. In fondo, si ottiene lo stesso risultato: per piccole distanze l'orologio rimane praticamente immutato, ma per grandi distanze il tic-tac si dilata sempre più...

Torniamo alla visione classica… Non vogliamo certo entrare nella metrica di Friedmann, Lemaitre e compagni, ci basta definire il fattore di scala R dell’espansione dell’Universo. Esso è legato al variare della distanza tra due oggetti dalla semplice relazione:

d(t)/do = R(t)/Ro    (dove “o” indica oggi)         …. (2)

Il modello cosmologico ci dice come R varia nel tempo. Applichiamolo al caso più semplice, quello lineare… avremmo che

R(t) = k · t

dR(t)/dt = k

la variazione sarebbe costante…

Facciamo adesso questo semplice ragionamento: immaginiamo due Achille che corrono alla stessa velocità lungo una certa direzione. La loro distanza rimane sempre la stessa. Chiamiamo il solito mago di turno e iniziamo a fare espandere lo spazio. Ne consegue che la distanza tra i due Achille, misurata, lungo la linea che stanno percorrendo, è obbligata ad aumentare. Possiamo dire che se il percorso si allunga di un certo fattore, lo stesso deve succedere alla distanza tra i due Achille (praticamente la relazione (2)).

Sostituiamo, adesso, i due Achille con due creste successive di una lunghezza d’onda. La loro separazione è esattamente la lunghezza d’onda e anch’essa deve aumentare in modo proporzionale al fattore di scala. Ne consegue una relazione eccezionale nella sua semplicità e ovvietà. Riprendiamo in mano la (1)

z = (λo – λe)/λe = λo/λe – 1

z + 1 = λo/λe

da quanto detto e dalla (2) diventa:

z +1 = Ro/R(t) = do/d(t)            …. (3)

Chiamata anche equazione di Lemaitre, essa permette di calcolare la relazione tra redshift e distanza  vincolata all’espansione dell’Universo (e, quindi, alla metrica che è tutta racchiusa dentro il fattore di scala).

Sintetizzando: il redshift di una galassia è una misura di quanto l’Universo si sia espanso tra il tempo dell’emissione della luce e il tempo in cui essa viene ricevuta da noi.

Sebbene le galassie non si muovano (a parte i trascurabili moti propri effettuati nello spazio), si può tuttavia DEFINIRE una velocità di recessione (v_r) che è la variazione rispetto al tempo della sua distanza.

v_r = ḋ (notate che il punto inserito sopra la d sta a significare la derivata di d rispetto al tempo).

A questa variazione corrisponde una variazione del fattore di scala R, che indico come Ṙ (derivata rispetto al tempo).

Il rapporto Ṙ/R deve essere per definizione proporzionale a ḋ/d

Lo possiamo dimostrare in modo quasi ridicolo partendo dalla (2)

d/do = R/Ro

d = (do/Ro)R

deriviamo ambo i membri rispetto al tempo

ḋ = (do/Ro)Ṙ

da cui…

ḋ/do = Ṙ/Ro

Mi sono quasi vergognato a scriverlo… ma la semplicità non è mai un difetto, anzi!

La velocità di recessione non è altri che ḋ, per cui

v_r = d Ṙ/R

ponendo

H = Ṙ/R

otteniamo la ben nota legge di Hubble

v_r =  H d

Possiamo perciò dire che H misura il tasso di espansione dell’Universo normalizzato al fattore di espansione. Questa descrizione permette di capire molto bene come H sia una costante “spaziale”, ma non certo temporale. Come già dimostrato precedentemente, anche se Ṙ fosse costante (variazione lineare) il valore di H varierebbe nel tempo: a mano a mano che R aumenta H diminuisce.

Facciamo nuovamente il caso più semplice con R lineare

R = k t

Ṙ = k

H = k/(kt) = 1/t

Aumentando il tempo t, ovviamente aumenta R e diminuisce la costante temporale H. Si nota subito che essa non è altro che l'inverso di un tempo, ossia una frequenza, il che ci riporta alla visione dell'espansione temporale: al crescere di R diminuisce la frequenza ossia aumenta la lunghezza d'onda.

In generale e in poche parole, l’espansione dell’Universo è descritta specificando (o scegliendo) la variazione del fattore di scala R.

Come fare, allora, per ricavare il redshift relativo alla luce di un oggetto che OGGI raggiunge la distanza di Hubble (ossia la cui luce non può più raggiungerci)?

Beh… basterebbe sapere qual era la distanza al momento della partenza della luce… e poi la relazione (3) ci darebbe il corrispondente redshift.

Per far questo, però, dovrei conoscere il fattore di scala o anche solo la costante di Hubble in quel momento. Purtroppo questo è un esercizio che va al di là dei nostri limiti (almeno per adesso) e dobbiamo accettare una soluzione semplicissima, ma grafica, che, però, ci permette, comunque, di imparare e di verificare direttamente molti concetti illustrati sia in questo articolo che in molti altri.

Immedesimiamoci in un’onda luminosa (il caro amico fotone non me ne voglia…) che lascia in un certo momento la stella o ciò che volete che, essendo immobile, è costretta a seguire la sua linea di Universo. Poniamo che questa linea si allontani dalla nostra con una velocità di recessione maggiore di quella della luce. L’oggetto che si trova su di essa, proprio perché è fermo, è costretto ad allontanarsi sempre più da noi a velocità superluminali a causa dell’espansione. Ma la luce che l’ha lasciata non è costretta a seguirlo e, anzi, ha una velocità fisica che le permette di lottare contro l’espansione (dal mondo degli dei, dove qualsiasi velocità era possibile, siamo passati al mondo umano dove le velocità hanno un limite).

E’ un po’ come se restasse a bagnomaria, cercando di venire verso di noi ma, nel contempo, trascinata verso l’esterno (i due famosi Achille…). Tuttavia, anche in queste condizioni critiche essa comincia a trovarsi su linee di Universo meno “veloci”, linee di Universo sempre meno distanti “angolarmente” da noi. La sua fatica dovuta alla costanza della sua velocità, allunga sempre di più la lunghezza d’onda, ma la lotta vede una via d’uscita.

Quando? Facile a dirsi. Quando si viene a trovare sulla linea che corrisponde alla velocità della luce (che è pur sempre uno spazio diviso un tempo). A questo punto, la strada è ancora faticosa, ma è ormai in discesa. La sua velocità supera quella di recessione “locale” e lei non fa altro che avvicinarsi a noi. Un lungo viaggio, una distanza tra i due Achille (le due creste che stabiliscono la lunghezza d’onda) che si è allargata di molto, ma alla fine eccola arrivare da noi giusta a 45°, in un diagramma spaziotemporale in cui ordinata e ascissa viaggiano di pari passo (anni e anni luce, ad esempio, o milioni di anni e milioni di anni luce).

Immaginiamo che quanto descritto sia il viaggio di un’onda emessa al momento della radiazione cosmica di fondo (praticamente il Big Bang…). L’oggetto (o quello che era) che l’ha emessa è scappato a velocità superluminale rispetto a noi e oggi si trova a una distanza mostruosa, ma ben conosciuta: il confine dell’Universo Osservabile (oggi calcolato in circa 46.5 miliardi di anni luce).

La sua luce, però, ci raggiunge comunque, attraverso quello che noi chiamiamo cono di luce passato. In modo molto intuitivo, anche se il destino dell’oggetto di partenza della luce era quello di viaggiare per sempre a velocità di recessione superluminale, la distanza tra luce emessa e noi era decisamente ancora piccola e la luce poteva combattere contro l’espansione. Non c‘è bisogno di disegnarlo, talmente lo conosciamo bene… e l’abbiamo anche costruito in modo più o meno empirico e approssimato, più di una volta. Questa volta, però, fidiamoci di una certa metrica che descrive con maggiore esattezza la situazione. Utilizziamo distanze e tempi propri e questo comporta deformazioni un po’ particolari su cui non possiamo certo addentrarci.

Potevo anche scegliere di semplificare la figura, ma avrei dovuto eseguire approssimazioni veramente brutali, magari più facili da seguire, ma tali da disegnare una situazione sicuramente lontana dalla realtà osservativa. Accettiamo, quindi, senza troppa fatica, delle linee di Universo che curvano un poco, così come un cono di luce più deformato di quanto, magari, abbiamo fatto in passato… se vogliamo guadagnare in semplicità, dobbiamo perdere in qualità e viceversa.

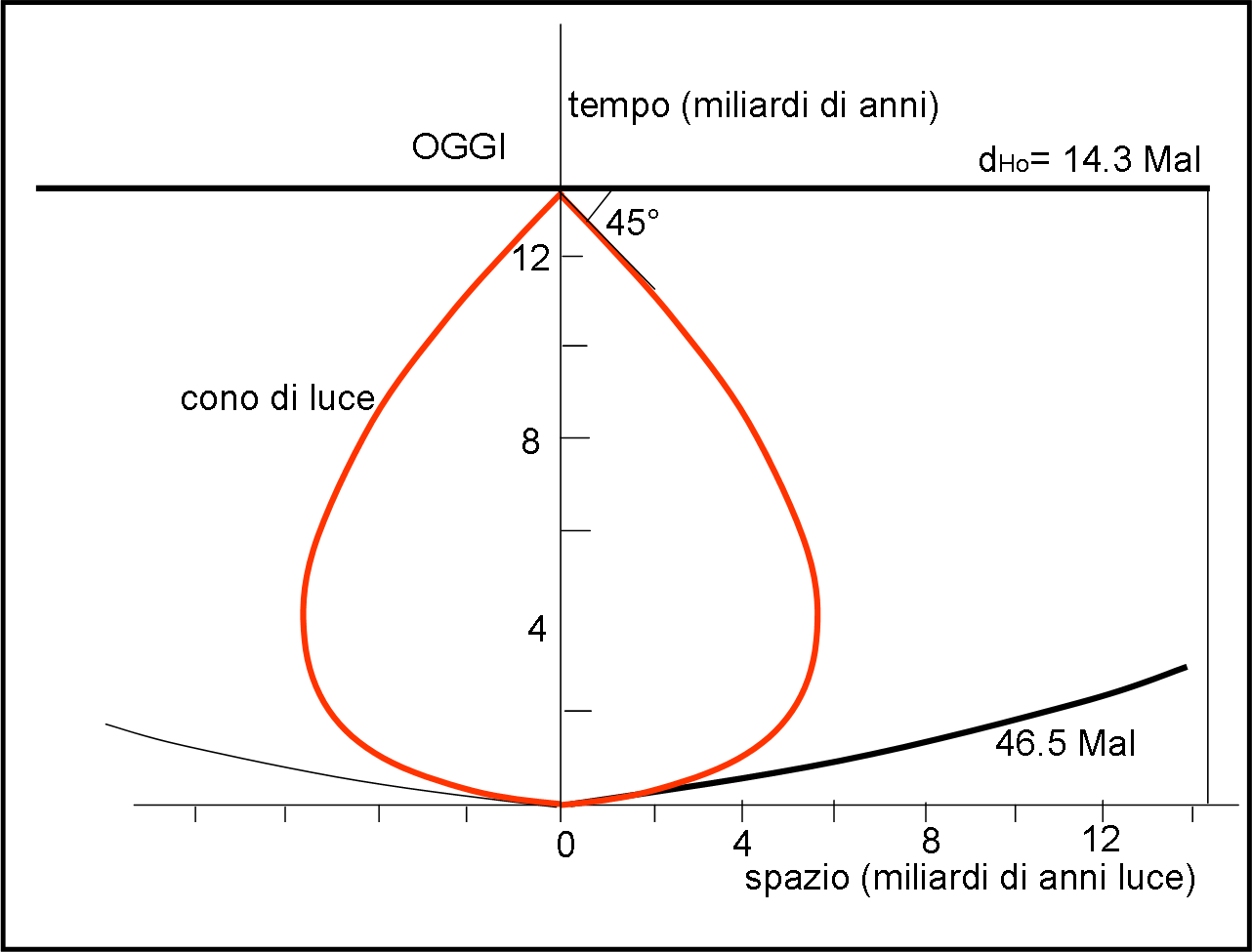
La Fig. 2 riporta solo e soltanto il cono di luce che raffigura la luce che riceviamo oggi e che proviene dalla prima emissione dell’Universo (il rumore cosmico di fondo).

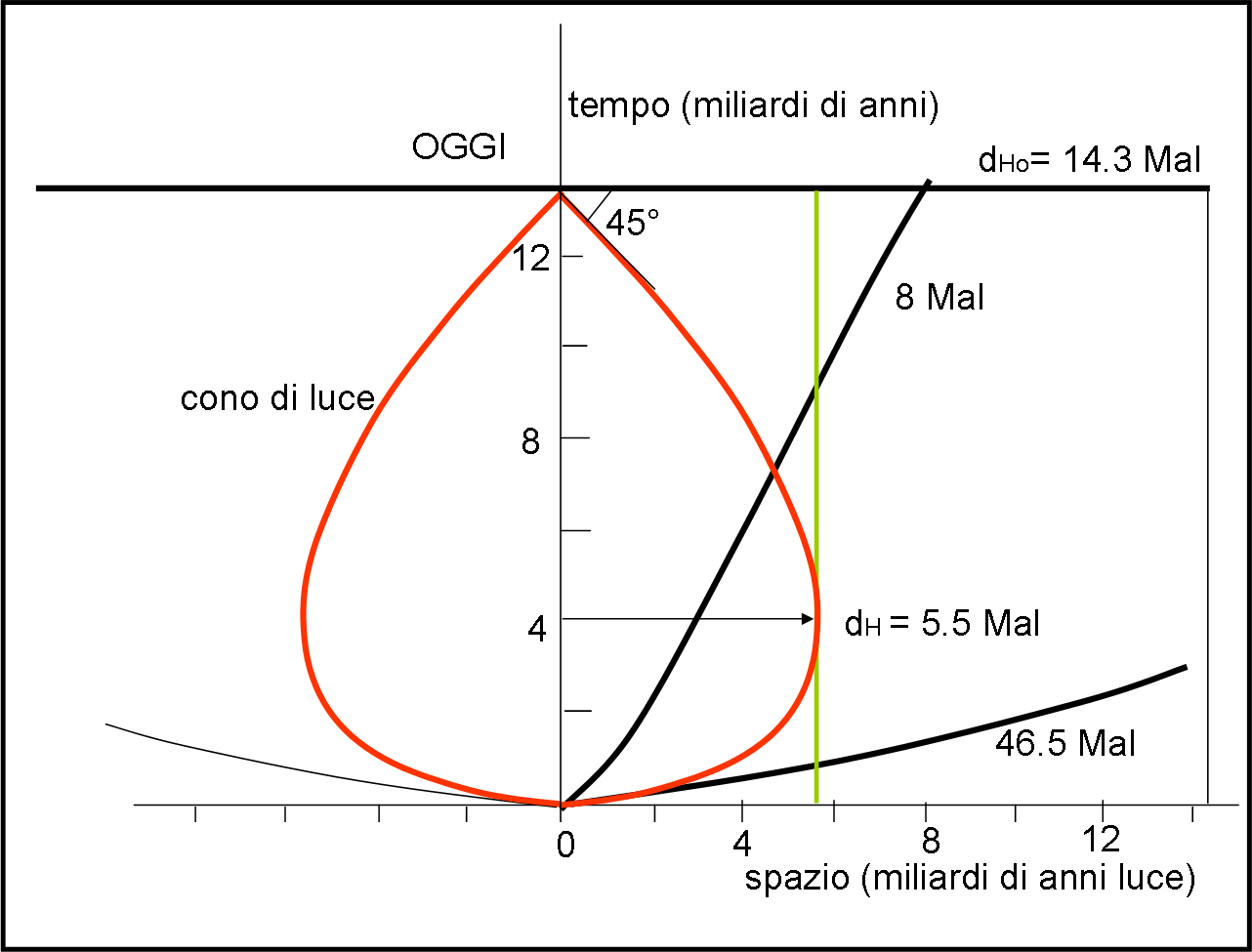
La linea di Universo che viaggia verso destra e sinistra è quella relativa, di conseguenza, all’Universo Osservabile di OGGI. L’intersezione con il tempo OGGI va fuori figura, ma noi indichiamo su di lei il valore che ha raggiunto oggi in termini di distanza spaziale, 46.5 miliardi di anni luce… Aggiungiamo anche, tanto per avere un'idea migliore della faccenda, la linea di Universo di un oggetto che ora si trova a 8 miliardi di anni luce da noi (ben all'interno della sfera di Hubble).

Un avvertimento: siamo nello spaziotempo, ma non possiamo certo applicare il diagramma di Minkowski e le sue divisioni. Non per niente, le due linee di Universo disegnate violano tranquillamente il principio di causalità e si trovano dove non potrebbe esistere nessun tragitto spaziotemporale. Per non fare troppi torti a Minkowski, notate, però,  che il cono di luce arriva a noi OGGI, proprio con linee rette inclinate di 45°. D’altra parte lo spaziotempo vicino a noi non risente praticamente dell’espansione (almeno per adesso).

Quanto rappresentato ci basta per rispondere graficamente alla quinta domanda.

Dove dovrebbe essere stata emessa la luce dell’oggetto che oggi si trova alla distanza di Hubble? Beh, proprio nel punto in cui finalmente la traiettoria della luce inviata dal rumore cosmico di fondo ha iniziato ad avvicinarsi a noi. Quel punto è proprio quello nel quale la velocità della luce inizia a guadagnare rispetto a quella di recessione. Tracciando la linea verticale verde, tangente al cono di luce, troviamo la distanza a cui deve essere partita la luce dell’oggetto che OGGI si trova alla distanza di Hubble. Righello... ed ecco il valore di circa 5.5 miliardi di anni luce (possiamo permetterci di non fare troppo i raffinati). Ma se l’emissione è avvenuta quando l’oggetto distava 5.5 miliardi di anni luce da noi e oggi quella distanza è diventata 14.3 miliardi di anni, abbiamo subito che:

z = 14.3/5.5 – 1 = 1.6

Questo reddshift  è il valore limite per essere ancora nel campo di osservabilità a tutt’oggi: un redshift più grande comporterebbe una posizione attuale al di là della distanza di Hubble.

Vediamo anche che questa luce è partita circa 4 miliardi di anni dopo il Big Bang. Ha quindi impiegato più di 9 miliardi di anni per arrivare a noi… Un bel viaggetto! Distava solo 5.5 miliardi di anni luce, ma per compierli ha impiegato quasi il doppio del tempo… Ah… questo Universo che si gonfia crea seri problemi ai nostri amici fotoni (come ci racconta questo piccolo fotone che ha viaggiato per 7,5 miliardi di anni prima di raggiungerci)! Però, abbiamo anche visto che la loro stanchezza non è proprio vera… è solo il loro orologio che ha rallentato.

Possiamo anche trovare subito il valore della costante di Hubble a quel tempo (qualcuno potrebbe dire : “Ma chi se ne frega?”… tuttavia è sempre un dato interessante che potrebbe innescare ulteriori riflessioni)…

Utilizziamo la solita formula (una specie di teorema di Pitagora della Cosmologia)

v_r = H d

H = v_r/d = c/d = 300 000/1689 = 178 km/s/Mpc     (1689 è la distanza espressa in megaparsec)

Beh… direi che può bastare così…

E' facile notare cosa implica la costanza di H  per un dato tempo... Ad esempio, per una distanza d di 1 solo Mpc, la velocità diventa esattamente uguale a 178 km/sec, proprio la costante di Hubble. Questa velocità aumenta a mano a mano che la distanza aumenta fino a diventare v = c per 1689 Mgp. D'altra parte H è uguale a una variazione di distanza (velocità) per un certo tempo diviso la  distanza e questo rapporto non può che essere costante in un certo istante t.

Notiamo comunque, come il viaggio della luce, l'allungamento della sua lunghezza d'onda, la lotta contro la corrente che cerca di trascinarla lontano, l'arrivo in condizioni di stabilità perfette, sono ingredienti perfetti per costruirci sopra una bella favola per bambini, ma non solo. Se, qualcuno vuole può anche provarci... abbiamo tanto bisogno di favole VERE. E questo tipo di semplificazione non distrugge certo la reputazione scientifica di chi la scrive, anzi... scrivere in modo semplice e chiaro lo consideriamo un valore aggiunto, non è scrivendo in modo difficile e oscuro che si mostra la propria bravura!

NEWS!! - La legge di Hubble ha ufficialmente cambiato nome, d'ora in poi di chiamerà LEGGE di HUBBLE-LEMAITRE. Il motivo ve lo raccontiamo QUI

Se vi è piaciuto questo NON-QUIZ, ne trovate altri QUI